Genelleştirilmiş Stokes teoremi - Generalized Stokes theorem

hakkında bir dizi makalenin bir parçası
kalkülüs
temel teorem Leibniz integral kuralı Fonksiyonların sınırları süreklilik Ortalama değer teoremi Rolle teoremi
Diferansiyel Tanımlar Türev  ( genellemeler ) Diferansiyel sonsuz küçük bir fonksiyonun Toplam kavramlar farklılaşma gösterimi İkinci türev örtük farklılaşma Logaritmik farklılaşma İlgili oranlar Taylor teoremi Kurallar ve kimlikler toplam Ürün Zincir Güç bölüm L'Hôpital kuralı Ters Genel Leibniz Faà di Bruno'nun formülü Reynolds
integral integral listeleri integral dönüşüm Tanımlar ters türev İntegral  ( yanlış ) Riemann integrali Lebesgue entegrasyonu Kontur entegrasyonu Ters fonksiyonların integrali Entegrasyon Parçalar diskler Silindirik kabuklar İkame  ( trigonometrik , Weierstrass , Euler ) Euler formülü Kısmi kesirler Değişen sıra Azaltma formülleri İntegral işareti altında farklılaşma risk algoritması
Dizi Geometrik  ( aritmetik-geometrik ) Harmonik dönüşümlü Güç binom Taylor yakınsama testleri Toplam limit (dönem testi) Oran Kök integral Doğrudan karşılaştırma Sınır karşılaştırması alternatif seri Cauchy yoğunlaşması Dirichlet Habil
Vektör Gradyan uyuşmazlık kıvırmak Laplacian Yönlü türev kimlikler teoremler Gradyan Yeşillik Stoklamak' uyuşmazlık genelleştirilmiş Stokes
çok değişkenli formalizmler Matris tensör Dış Geometrik Tanımlar Kısmi türev Çoklu integral çizgi integrali Yüzey integrali hacim integrali Jacobian kendir
İhtisas kesirli mallivin stokastik Varyasyonlar
Çeşitli ön kalkülüs Tarih Sözlük konu listesi Entegrasyon Arı analiz
v T e

Olarak vektör, diş taşı ve diferansiyel geometri genelleştirilmiş Stokes teoremi (bazen kesme işareti ile Stokes teoremi veya Stokes teoremi ) olarak da adlandırılan Stokes-Cartan teoremi , yaklaşık bir ifadedir entegrasyon bölgesinin ayırıcı formları ile ilgili manifoldlar , basitleştirir ve genelleştirir de birkaç teoremi gelen vektör hesabı . İki boyutlu çizgi integrallerini üç boyutlu yüzey integralleriyle ilişkilendiren Isaac Newton'un temel kalkülüs teoreminin bir genellemesidir .

Stokes teoremi bir diferansiyel formu ayrılmaz söylüyor w üzerinde sınır bazılarının yönlendirilebilir manifoldu Q onun integrali eşittir dış türev dco bütün üzerinde Q yani,

${\displaystyle \int _{\kısmi \Omega }\omega =\int _{\Omega }d\omega \,.}$

Stokes teoremi, Vito Volterra , Édouard Goursat ve Henri Poincaré tarafından vektör hesabı teoremlerinin genelleştirilmesi üzerine daha önceki çalışmaların ardından 1945'te Élie Cartan tarafından modern biçiminde formüle edildi .

Stokes Bu modern formu teorem geniş bir genellemedir klasik sonucu olduğunu Lord Kelvin tebliğ George Stokes 2 Temmuz tarihli bir mektupta, 1850 Stokes 1854 tarihinde bir soru olarak teoremi set Smith'in Ödülü sonucu doğurmuştur sınav, adını taşıyan. Bu bileşik ilk olarak yayınlanan Hermann Hankel 1861 Bu, klasik olarak teoremi Kelvin Stokes ilgilidir yüzey integralinin ait kıvrım a vektör alanına F (bir yüzey boyunca akı ve kıvırmak F için Öklid üç alanda) hattı integrali vektör alanının sınırının üzerindedir (döngü integrali olarak da bilinir).

Basit klasik vektör analizi örneği

Let γ : [ a , b ] → R ' ² olduğu bir parçalı yumuşak Ürdün düzlem eğrisi . Jordan eğri teoremi ima γ bölme R ² , iki içine bileşenler, bir kompakt bir ve kompakt olmayan bir başka. Let D tarafından sınırlanmaktadır sıkı bir kısmını ifade y ve varsayalım ψ : D → R ³ ile pürüzsüz olan S  =: ψ ( D ) . Eğer Γ olan alan eğrisi tarafından tanımlanan y ( t ) = ψ ( γ ( t )) ve F düzgün bir vektör alanı olan R ³ , o zaman:

${\displaystyle \oint _{\Gamma }\mathbf {F} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\nabla \times \mathbf {F} \,\cdot \,d\mathbf {S} }$

Bu klasik ifade, vektör alanının 1-form ile ve curl ile iki form ile bir tanımlaması yapıldıktan sonra yukarıda belirtilen genel formülasyonun özel bir halidir.

${\displaystyle {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\\\end{pmatrix}}\cdot d\Gamma \to F_{x}\,dx+F_{ y}\,dy+F_{z}\,dz}$

${\displaystyle \nabla \times {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\end{pmatrix}}\cdot d\mathbf {S} ={\başlangıç{pmatrix} \partial _{y}F_{z}-\partial _{z}F_{y}\\\partial _{z}F_{x}-\partial _{x}F_{z}\\\partial _{ x}F_{y}-\partial _{y}F_{x}\\\end{pmatrix}}\cdot d\mathbf {S} \to }$

${\displaystyle d(F_{x}\,dx+F_{y}\,dy+F_{z}\,dz)=(\partial _{y}F_{z}-\partial _{z}F_{ y})\,dy\wedge dz+(\partial _{z}F_{x}-\partial _{x}F_{z})\,dz\wedge dx+(\partial _{x}F_{y}- \partial _{y}F_{x})\,dx\kama dy}$.

Kalkülüsün temel teoreminin diverjans teoremi ve Green teoremi gibi diğer klasik genellemeleri, vektör alanlarının diferansiyel formlarla standart bir tanımlamasını yaptıktan sonra yukarıda belirtilen genel formülasyonun özel durumlarıdır (klasik teoremlerin her biri için farklıdır).

Tanıtım

Taşı temel teoremi olduğu durumları yekpare bir fonksiyonu f fazla aralık [ a , b ] bir bulgu hesaplanabilir İlkel F arasında  f :

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a)\,.}$

Stokes teoremi, aşağıdaki anlamda bu teoremin geniş bir genellemesidir.

• F seçeneği ile , dF/dx= f ( x ) . Arasında dilinde diferansiyel formları , bu söylüyor f ( x ) dx olan dış türev 0-formda, yani fonksiyonu, F : başka bir deyişle, bu dF = f dx . Genel Stokes teoremi , F gibi sadece 0-formlar yerine daha yüksek diferansiyel formlar ω için geçerlidir .
• Kapalı bir aralık [ a , b ] , sınırı olan tek boyutlu bir manifoldun basit bir örneğidir . Sınırı, a ve b noktalarından oluşan kümedir . Entegre f aralığı boyunca daha yüksek boyutlu bir manifold formları entegre şekilde genelleştirilebilir. İki teknik koşul gereklidir: manifold yönlendirilebilir olmalı ve iyi tanımlanmış bir integral vermek için form kompakt olarak desteklenmelidir .
• a ve b noktaları kapalı aralığın sınırını oluşturur. Daha genel olarak, Stokes teoremi , sınır ile yönlendirilmiş manifoldlar M için geçerlidir . Sınır ∂ M arasında M bir manifold ve devralır bu doğal bir yönelim kendisidir M . Örneğin, aralığın doğal yönelimi, iki sınır noktasının yönelimini verir. Sezgisel olarak, a , aralığın karşıt uçlarında oldukları için b olarak zıt yönelimi devralır . Yani, iki sınır noktası a , b üzerinde F'yi "entegre etmek" , F ( b ) − F ( a ) farkını alıyor .

Daha basit terimlerle, noktalar eğrilerin sınırları, yani 1 boyutlu manifoldların 0 boyutlu sınırları olarak düşünülebilir. Bu nedenle, tek bir (tamamlayıcı değerini bulmak gibi f dx = dF 1-boyutlu manifoldu üzerinde) ( [ a , b ] (anti-türevi alınarak) F 0 boyutlu sınırlarında) ( { a , b }), ( n − 1'deki ters türevi ( ω ) dikkate alarak , integrallerin ( dω ) n boyutlu manifoldlar ( Ω ) üzerindeki değeriyle ilgilenmek için birkaç ek uyarı ile kalkülüsün temel teoremi genelleştirilebilir. ) manifoldun -boyutlu sınırları ( ∂Ω ).

Yani temel teorem okur:

${\displaystyle \int _{[a,b]}f(x)\,dx=\int _{[a,b]}\,dF=\int _{\{a\}^{-}\cup \{b\}^{+}}F=F(b)-F(a)\,.}$

Sınırlı düz manifoldlar için formülasyon

Let Ω bir olmak yönlendirilmiş düz manifoldu sınır ile boyut , n ve izin α bir olmak düz N - farklı form olan kompakt desteklenen ilgili Q . İlk olarak, α'nın tek, yönlendirilmiş bir koordinat grafiğinin { U , φ } alanında kompakt olarak desteklendiğini varsayalım . Bu durumda, integralini tanımlar a fazla Q olarak

yani yoluyla geri çekilme ve a kadar R ⁿ .

Daha genel olarak, α bölü Ω'un integrali şu şekilde tanımlanır: { ψ _i } (tutarlı olarak yönlendirilmiş) koordinat çizelgelerinin yerel olarak sonlu bir örtüsü { U _i , φ _ben } ile ilişkili birliğin bir bölümü olsun , sonra integrali tanımlayın

burada toplamı, her bir terimin için geri çekerek değerlendirilir R ^n, yukarıda tarif edildiği gibi. Bu miktar iyi tanımlanmıştır; yani, koordinat çizelgelerinin seçimine veya birliğin bölünmesine bağlı değildir.

Genelleştirilmiş Stokes teoremi şöyledir:

Geleneksel olarak, olarak kısaltılır , çünkü dahil etme haritası tarafından bir diferansiyel formun geri çekilmesi, basitçe onun etki alanıyla sınırlandırılmasıdır: . Burada bir dış türev sadece manifoldu yapısı kullanılarak tanımlanmıştır. Sağ taraf bazen -manifoldun sınırı olmadığı gerçeğini vurgulamak için yazılır . (Bu gerçek aynı zamanda Stokes teoreminin bir anlamıdır, çünkü belirli bir düz boyutlu manifold için , teoremin iki kez uygulanması herhangi bir -formu verir , bu da şunu ima eder .) Denklemin sağ tarafı genellikle formüle etmek için kullanılır. integral yasalar; sol taraf daha sonra eşdeğer diferansiyel formülasyonlara yol açar (aşağıya bakınız). ${\textstyle \int _{\kısmi \Omega }i^{*}\omega }$${\textstyle \int _{\kısmi \Omega }\omega }$${\displaystyle i^{*}\omega =\omega |_{\kısmi \Omega }}$${\görüntüleme stili d}$${\textstyle \oint _{\kısmi \Omega }\omega }$${\görüntüleme stili (n-1)}$${\görüntüleme stili \kısmi \Omega }$${\görüntüleme stili n}$${\görüntüleme stili\Omega }$${\textstyle \int _{\partial (\partial \Omega )}\omega =\int _{\Omega }d(d\omega )=0}$${\görüntüleme stili (n-2)}$${\ Displaystyle \ omega }$${\displaystyle \partial (\partial\Omega )=\emptyset }$

Teorem genellikle , üzerinde formun tanımlandığı daha büyük bir manifoldun gömülü yönlendirilmiş bir alt manifoldu olduğu durumlarda kullanılır . ${\görüntüleme stili\Omega }$${\displaystyle \mathbf {R} ^{k}}$${\ Displaystyle \ omega }$

Topolojik ön bilgiler; zincirler üzerinden entegrasyon

Let M bir olmak pürüzsüz manifoldu . A (yumuşak) bir tekil k -simplex olarak M , bir olarak tanımlanan düz harita standart simpleks R, ^k için M . Grup C _k ( E , Z ) tekil k - zincirleri üzerinde M olarak tanımlanır serbest değişmeli grup tekil setinde k olarak -simplices M . Bu gruplar, ∂ sınır haritasıyla birlikte bir zincir kompleksi tanımlar . Karşılık gelen homoloji (sırasıyla. Kohomolojisi) grubunun oluşturulması bilinen izomorf tekil homoloji grubu , H _{, k} ( E , Z ) (sırasıyla. Tekil cohomoloji grubu H ^k ( E , Z ) ) düz simplices yerine sürekli kullanılarak tanımlanır, M .

Öte yandan, bağlantı haritası olarak dış türevi, d olan diferansiyel formlar, de Rham kohomoloji gruplarını H tanımlayan bir ortak zincir kompleksi oluşturur.^k
_dR( M , R ) .

Diferansiyel k- formları, R ^k'ye geri çekilerek doğal bir şekilde bir k- simplex üzerinde entegre edilebilir . Doğrusallıkla genişletme, birinin zincirler üzerinden bütünleşmesine izin verir. Bu, alan, doğrusal bir ilk verir k için -biçimleri k tekil cochains th grubu, Cı- ^k ( E , Z ) , lineer fonksiyoneller Cı _k ( E , Z ) . Başka bir deyişle, bir k -formu ω bir fonksiyoneli tanımlar.

üzerinde k zincirleri. Stokes teoremi bunun de Rham kohomolojisinden tekil kohomolojiye gerçek katsayılı bir zincir haritası olduğunu söylüyor; Dış türev, d , gibi davranır ikili arasında ∂ formlara. Bu, de Rham kohomolojisinden tekil kohomolojiye bir homomorfizm verir. Formlar düzeyinde, bu şu anlama gelir:

1. kapalı formlar, yani, dω = 0 , sınırlar üzerinde , yani ∂Σ _c M _c olarak yazılabilen manifoldlar üzerinde sıfır integrale sahiptir ve
2. tam formlar, yani ω = dσ , döngüler üzerinde sıfır integrale sahiptir , yani sınırların toplamı boş kümeye eşitse : Σ _c M _c = ∅ .

De Rham teoremi , bu homomorfizmin aslında bir izomorfizm olduğunu gösterir . Yani yukarıdaki 1 ve 2'nin tersi doğrudur. Diğer bir deyişle, { C _ı } döngüleri üreten k inci homoloji grubu, daha sonra karşılık gelen herhangi bir gerçek sayılar için, { bir _ı } , kapalı bir form bulunmaktadır mevcut Q'dan şekilde,

ve bu form kesin formlara kadar benzersizdir.

Düz manifoldlar üzerindeki Stokes teoremi, düz manifoldlardaki zincirler için Stokes teoreminden türetilebilir ve bunun tersi de geçerlidir. Resmi olarak belirtilen, ikincisi okur:

Temel ilke

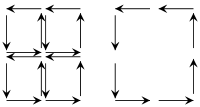
Bu topolojik argümanları basitleştirmek için, d = 2 boyutları için bir örnek göz önünde bulundurarak temel prensibi incelemeye değer . Ana fikir, bir manifoldun yönlendirilmiş bir döşemesinde, iç yolların zıt yönlerde geçtiğini gösteren soldaki diyagram ile anlaşılabilir; yol integraline katkıları böylece birbirlerini ikili olarak iptal eder. Sonuç olarak, yalnızca sınırdan gelen katkı kalır. Bu nedenle, Stokes teoremini , genellikle zor olmayan, yeterince ince döşemeler (veya eşdeğerde, basitler ) için kanıtlamak yeterlidir .

Kaba kümelere genelleme

Ω'un sınırı olan düzgün bir manifold olduğu yukarıdaki formülasyon birçok uygulamada yeterli değildir. Örneğin, entegrasyon alanı iki x koordinatı ile iki fonksiyonun grafikleri arasındaki düzlem bölge olarak tanımlanırsa , genellikle alanın köşeleri olur. Böyle bir durumda, köşe noktaları, Ω'un sınırı olan düzgün bir manifold olmadığı anlamına gelir ve bu nedenle yukarıda verilen Stokes teoreminin ifadesi geçerli değildir. Yine de Stokes teoreminin sonucunun hala doğru olduğunu kontrol etmek mümkündür. Bunun nedeni, Ω ve sınırının küçük bir nokta kümesinden (bir ölçü sıfır kümesi) uzakta iyi davranmış olmasıdır .

Stokes teoreminin pürüzlülüğe izin veren bir versiyonu Whitney tarafından kanıtlandı. D' nin, R ^n'nin bağlı bir sınırlı açık alt kümesi olduğunu varsayalım . Çağrı D bir standart alan eğer biri aşağıdaki özelliği: bir alt duyulmaktadır P arasında ∂ D açık, ∂ D tamamlayıcı olarak, ∂ D sahiptir Hausdorff ( n - 1) Birleştirilmiş sıfır; ve öyle ki P'nin her noktası bir genelleştirilmiş normal vektöre sahiptir . Bu bir v ( x ) vektörüdür , öyle ki, v ( x ) birinci temel vektör olacak şekilde bir koordinat sistemi seçilirse , o zaman x civarında açık bir komşulukta , düzgün bir f ( x ₂ , ..) fonksiyonu vardır . ., x _n ) öyle ki P { x ₁ = f ( x ₂ , ..., x _n ) } grafiği ve D bölgesi { x ₁  : x ₁ < f ( x ₂ , ..., x) _n ) } . Whitney standart etki alanının sınır sıfır Hausdorff bir dizi birliği olduğu açıklamalar ( n - 1) sayılmış ve pürüzsüz bir sonlu ya da sayılabilir birlik ( n - 1), sadece bir ilgili alan, her biri -manifolds, yan. Daha sonra, eğer kanıtlamaktadır D bir standart alan olan R ^{, n} , ω bir olan ( n- 1 -) , sürekli tanımlandığı gibidir ve üzerinde bağlanmış olan -formunu D ∪ P ile pürüzsüz, D , ilgili integrali P ve bu tip dco olan D üzerinde integrallenebilir , o zaman Stokes teoremi geçerlidir, yani,

${\displaystyle \int _{P}\omega =\int _{D}d\omega \,.}$

Kaba kümelerin ölçü-teorik özelliklerinin incelenmesi, geometrik ölçü teorisine yol açar . Stokes teoreminin daha da genel versiyonları Federer ve Harrison tarafından kanıtlanmıştır.

Özel durumlar

Diferansiyel formları kullanan Stokes teoreminin genel formu, özel durumlardan daha güçlü ve kullanımı daha kolaydır. Geleneksel versiyonlar, diferansiyel geometri makinesi olmadan Kartezyen koordinatlar kullanılarak formüle edilebilir ve bu nedenle daha erişilebilirdir. Ayrıca, daha yaşlılar ve sonuç olarak isimleri daha tanıdık. Geleneksel formlar, bilim adamları ve mühendisler tarafından genellikle daha uygun olarak kabul edilir, ancak geleneksel formülasyonun doğal olmadığı, diğer koordinat sistemleri, hatta küresel veya silindirik koordinatlar gibi tanıdık olanlar bile kullanıldığında ortaya çıkar. İsimlerin uygulanma biçiminde ve ikili formülasyonların kullanımında karışıklık potansiyeli vardır.

Kelvin-Stokes teoremi

Bu, 1 form için (ikileştirilmiş) (1 + 1) boyutlu bir durumdur ( vektör alanları hakkında bir ifade olduğu için çiftleştirilmiştir ). Bu özel durum, çoğu kez, üniversiteye giriş niteliğindeki birçok vektör kalkülüs dersinde Stokes teoremi olarak anılır ve fizik ve mühendislikte kullanılır. Bazen kıvrılma teoremi olarak da bilinir .

Klasik Kelvin-Stokes teoremi ilgilidir yüzey integralinin ait kıvrım a vektör alanına bir yüzey üzerinde Σ üç uzay Öklid olarak hat integrali sınırının üzerinden vektör alanının. Öklid 3-uzayda metriği kullanarak 1-formlu bir vektör alanını tanımladığımızda , bu genel Stokes teoreminin ( n = 2 ile ) özel bir halidir . Çizgi integrali, eğri ∂Σ , pozitif olması gerekir yönünü , yani ∂Σ noktaları zaman saat yönü tersinde yüzey normali , n izleyiciye, sayı.

Kelvin–Stokes teoreminin bir sonucu, sıfır kıvrımlı bir vektör alanının alan çizgilerinin kapalı konturlar olamamasıdır. Formül şu şekilde yeniden yazılabilir:

Green teoremi

Green teoremi , yukarıda belirtilen P , Q ve R cinsinden integralde her iki tarafın üçüncü integrali olarak hemen tanınabilir .

elektromanyetizmada

Dört Maxwell denkleminden ikisi, 3-D vektör alanlarının kıvrımlarını içerir ve bunların diferansiyel ve integral formları Kelvin-Stokes teoremi ile ilişkilidir . Hareketli sınırları olan durumlardan kaçınmak için dikkatli olunmalıdır: kısmi zaman türevlerinin bu tür durumları hariç tutması amaçlanmıştır. Hareketli sınırlar dahil edilirse, entegrasyon ve farklılaşmanın değişimi, aşağıdaki sonuçlara dahil edilmeyen sınır hareketi ile ilgili terimleri ortaya çıkarır (bkz . İntegral işareti altında farklılaşma ):

İsim	diferansiyel formu	İntegral form (Kelvin–Stokes teoremi artı göreli değişmezlik kullanılarak, ∫∂/∂ t ... → NS/dt∫ ... )
Maxwell-Faraday denklemi Faraday indüksiyon yasası :	${\displaystyle \quad \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\dörtlü }$	${\displaystyle {\begin{aligned}\quad \oint _{C}\mathbf {E} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {E} \cdot d \mathbf {A} \\&=-\iint _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A} \end{hizalı}}\quad }$( C ve S'nin sabit olması gerekmez)
Ampère yasası (Maxwell'in uzantısıyla):	${\displaystyle \quad \nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\kısmi t}}\dört }$	${\displaystyle {\begin{aligned}\quad \oint _{C}\mathbf {H} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {H} \cdot d \mathbf {A} \\&=\iint _{S}\mathbf {J} \cdot d\mathbf {A} +\iint _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot d\mathbf {A} \end{hizalı}}\dörtlü }$( C ve S'nin sabit olması gerekmez)

Maxwell denklemlerinin yukarıda listelenen alt kümesi, SI birimlerinde ifade edilen elektromanyetik alanlar için geçerlidir . CGS veya Gauss birimleri gibi diğer birim sistemlerinde , terimler için ölçeklendirme faktörleri farklıdır. Örneğin, Gauss birimlerinde, Faraday'ın indüksiyon yasası ve Ampère yasası şu biçimleri alır:

${\displaystyle {\begin{hizalanmış}\nabla \times \mathbf {E} &=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\ ,,\\\nabla \times \mathbf {H} &={\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}+{\frac {4\ pi }{c}}\mathbf {J} \,,\end{hizalı}}}$

sırasıyla, burada C olan ışık hızı vakumla.

diverjans teoremi

Aynı şekilde, diverjans teoremi

${\displaystyle \int _{\mathrm {Vol} }\nabla \cdot \mathbf {F} \,d_{\mathrm {Vol} }=\oint _{\partial \operatöradı {Cilt} }\mathbf {F} \cdot d{\boldsymbol {\Sigma }}}$

vektör alanını Öklid hacim formuyla daraltarak elde edilen ( n − 1) -formuyla bir vektör alanını tanımlarsak özel bir durumdur . Bunun bir uygulaması, c'nin keyfi bir sabit vektör olduğu F = f c durumudur . Ürünün diverjansını çözmek

${\displaystyle \mathbf {c} \cdot \int _{\mathrm {Cilt} }\nabla f\,d_{\mathrm {Cilt} }=\mathbf {c} \cdot \oint _{\partial \mathrm { Cilt} }f\,d{\boldsymbol {\Sigma }}\,.}$

Bu bulduğumuz tüm c için geçerli olduğundan

${\displaystyle \int _{\mathrm {Cilt} }\nabla f\,d_{\mathrm {Cilt} }=\oint _{\partial \mathrm {Cilt} }f\,d{\boldsymbol {\Sigma } }\,.}$

Ayrıca bakınız

• Chandrasekhar-Wentzel lemması

Dipnotlar

Referanslar

daha fazla okuma

• Grunsky, Helmut (1983). Genel Stokes Teoremi . Boston: Pitman. ISBN'si 0-273-08510-7.
• Katz, Victor J. (Mayıs 1979). "Stokes Teoreminin Tarihi". Matematik Dergisi . 52 (3): 146–156. doi : 10.2307/2690275 . JSTOR  2690275 .
• Loomis, Lynn Harold ; Sternberg, Shlomo (2014). Gelişmiş Hesap . Hackensack, New Jersey: Dünya Bilimsel. ISBN'si 978-981-4583-93-0.
• Madsen, Ib ; Tornehave, Jørgen (1997). Matematikten Kohomolojiye: De Rham kohomolojisi ve karakteristik sınıfları . Cambridge, Birleşik Krallık: Cambridge University Press. ISBN'si 0-521-58956-8.
• Marsden, Jerrold E .; Anthony, Tromba (2003). Vektör Analizi (5. baskı). W. H. Freeman.
• Lee, John (2003). Düzgün Manifoldlara Giriş . Springer-Verlag. ISBN'si 978-0-387-95448-6.
• Rudin, Walter (1976). Matematiksel Analiz İlkeleri . New York, NY: McGraw-Hill. ISBN'si 0-07-054235-X.
• Spivak, Michael (1965). Manifoldlar Üzerine Hesap: İleri Kalkülüsün Klasik Teoremlerine Modern Bir Yaklaşım . San Francisco: Benjamin Cummings. ISBN'si 0-8053-9021-9.
• Stewart, James (2009). Matematik: Kavramlar ve Bağlamlar . Cengage Öğrenme. s. 960–967. ISBN'si 978-0-495-55742-5.
• Stewart, James (2003). Matematik: Erken Aşkın Fonksiyonlar (5. baskı). Brooks/Cole.
• Tu, Loring W. (2011). Manifoldlara Giriş (2. baskı). New York: Springer. ISBN'si 978-1-4419-7399-3.

Dış bağlantılar

• İlgili Medya Stokes teoremi Wikimedia Commons
• "Stokes formülü" , Matematik Ansiklopedisi , EMS Press , 2001 [1994]
• Diverjans Teoremi ve Stokes Teoreminin Kanıtı
• Calculus 3 – lamar.edu'dan Stokes Teoremi – açıklayıcı bir açıklama
• "Manifoldlar üzerinde Stokes Teoremi" . Alef Sıfır . 3 Mayıs 2020 – YouTube üzerinden .