Kuaterniyon grubu - Quaternion group

Cebirsel yapı → Grup teorisi Grup teorisi
Temel kavramlar alt grup Normal alt grup bölüm grubu (Yarı-) direkt ürün Grup homomorfizmaları çekirdek resim doğrudan toplam çelenk ürünü basit sonlu sonsuz sürekli çarpımsal katkı döngüsel değişmeyen dihedral nilpotent çözülebilir eylem Grup teorisi sözlüğü grup teorisi konularının listesi
sonlu gruplar Sonlu basit grupların sınıflandırılması döngüsel dönüşümlü yalan türü sporadik Cauchy teoremi Lagrange teoremi Sylow teoremleri Hall teoremi p grubu Temel değişmeli grup Frobenius grubu Schur çarpanı Simetrik grup S n Klein dört grup V Dihedral grup D n Kuaterniyon grubu Q Disiklik grup Dic n
ayrık gruplar kafesler Tamsayılar ( )${\displaystyle \mathbb {Z} }$ Ücretsiz grup Modüler gruplar PSL(2, )${\displaystyle \mathbb {Z} }$ SL(2, )${\displaystyle \mathbb {Z} }$ aritmetik grubu kafes hiperbolik grup
Topolojik ve Lie grupları solenoid Daire Genel doğrusal GL( n ) Özel doğrusal SL( n ) Ortogonal O( n ) Öklid E( n ) Özel ortogonal SO( n ) Üniter U( n ) Özel üniter SU( n ) Simplektik Sp( n ) G, 2 F 4 E 6 E 7 E 8 Lorentz poincare konformal difeomorfizm Döngü Sonsuz boyutlu Lie grubu O(∞) SU(∞) Sp(∞)
cebirsel gruplar Doğrusal cebir grubu indirgeyici grup değişmeli çeşit eliptik eğri
v T e

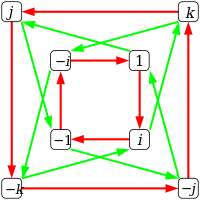
Q _8'in döngü diyagramı . Her renk, e = 1 kimlik elemanına bağlı herhangi bir elemanın bir dizi gücünü belirtir. Örneğin, kırmızı döngü i ² = e , i ³ = i ve i ⁴ = e olduğu gerçeğini yansıtır . Kırmızı döngü ayrıca i ² = e , i ³ = i ve i ⁴ = e olduğunu da yansıtır .

Gelen grup teorisi , Dördey grubu S ₈ (bazen sadece Q ile gösterilen) gömlek bir olan olmayan değişmeli grubu arasında sırayla sekiz elemanı alt-izomorf sekiz, arasında quaternions çarpma altında. Grup sunumu ile verilmektedir.${\görüntüleme stili \{1,i,j,k,-1,-i,-j,-k\}}$

${\displaystyle \mathrm {Q} _{8}=\langle {\bar {e}},i,j,k\mid {\bar {e}}^{2}=e,\;i^{2 }=j^{2}=k^{2}=ijk={\bar {e}}\rangle ,}$

burada e elementi ve bir E yolculukları grubun diğer elemanları ile.

Başka S sunumu ₈ olduğu

${\displaystyle \mathrm {Q} _{8}=\langle a,b\mid a^{4}=e,a^{2}=b^{2},ba=a^{-1}b\ aralık.}$

Dihedral grupla karşılaştırıldığında

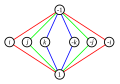
Kuaternion Q grubu ₈ ile aynı düzene sahip dihedral grubu D ₄ bunların Cayley ve döngü grafikler ile gösterildiği gibi, ancak farklı bir yapı,:

	S 8	D 4
Cayley grafiği	Kırmızı oklar g → gi'yi , yeşil g → gj'yi bağlar .
döngü grafiği

D diyagramlarda ₄ , grup elemanları tanımlamak temsili bir F harfi üzerindeki etkileri ile işaretlenmiştir R ² . Aynı Q için yapılamaz ₈ bu hiçbir şekilde sunumunu sahip olduğu için, R ² veya R ³ . D ₄ , bölünmüş kuaterniyonların bir alt kümesi olarak gerçekleştirilebilir , aynı şekilde Q ₈ kuaterniyonların bir alt kümesi olarak görülebilir.

çay masası

Cayley Tablo Q (çarpma tablo) ₈ ile verilmektedir:

Özellikler

Bu Not I , j ve k her sahip düzeni Q dört ₈ ve bunlardan herhangi iki tüm grup oluşturur. Bu fazlalığı atlamak için yalnızca iki öğeye dayanan Q _8'in başka bir sunumu :

${\displaystyle \langle x,y\mid x^{4}=1,x^{2}=y^{2},y^{-1}xy=x^{-1}\rangle .}$

Örneğin , ve alabilir . ${\görüntüleme stili i=x,j=y}$${\görüntüleme stili k=xy}$

Kuaternion grubu olduğu olağan dışı bir özelliğe sahiptir Hamiltonyenin S: ₈ -olmayan değişmeli, ama her bir alt grubu olan , normal . Her Hamiltonian grubu, Q _8'in bir kopyasını içerir .

Kuaterniyon grubu Q ₈ ve dihedral grup D ₄ , nilpotent değişmeyen olmayan grubun en küçük iki örneğidir .

Merkezi ve komütatör alt grup Q'nun ₈ alt grubudur . İç otomorfizm grubu Q ₈ grubu ile verilir merkez örneğin, modulo faktör grubu S ₈ / {E, E olup}, izomorf için Klein dört grup V tam otomorfizm grubu Q'nun ₈ olan izomorfik için S ₄ , simetrik grup dört harfinden (bakınız The Matrix temsilleri altında) ve dış otomorfizma grubu Q'nun ₈ böylece olarak S ₄ S izomorf / V, ₃ . ${\displaystyle \{e,{\bar {e}}\}}$

Kuaternion Q grubu ₈ , beş eşlenik sınıfları, {e}, {sahiptir , e }, {ı, ı }, {j, j }, {k, k } ve çok beş indirgenemez temsilleri boyutları 1 ile karmaşık sayılar üzerinde, 1,1,1,2:

önemsiz temsil

i,j,k-çekirdekli işaret temsilleri : Q _8'in üç maksimum normal alt grubu vardır: sırasıyla i, j ve k tarafından oluşturulan döngüsel alt gruplar. Her maksimal normal alt grup N için , 2 elemanlı bölüm grubu G / N aracılığıyla çarpanlara ayırma tek boyutlu bir temsil elde ederiz . Temsil, N'nin öğelerini 1'e ve N'nin dışındaki öğeleri -1'e gönderir .

2 boyutlu gösterim : Aşağıda Matriks gösterimlerinde açıklanmıştır .

Karakter tablosu Q'nun ₈ döner üzerinden D'nin aynı olduğu ₄ :

İndirgenemez karakterleri yana sıralar halinde yukarıdaki gerçek değerlere sahip, bu verir ayrışma gerçek bir grup cebir ait asgari iki taraflı içine idealleri : , İdempotentler : irreducibles karşılık böylece,${\displaystyle \chi _{\rho }}$${\ Displaystyle G=Q_{8}}$${\displaystyle \textstyle \mathbb {R} [Q_{8}]\ =\ \bigoplus _{\rho }(e_{\rho })}$ ${\displaystyle e_{\rho }\in \mathbb {R} [Q_{8}]}$${\displaystyle \textstyle e_{\rho }={\frac {\dim(\rho )}{|G|}}\sum _{g\in G}\chi _{\rho }(g^{-1 })G}$

${\displaystyle e_{\text{triv}}={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}+j+{\bar {j}}+ k+{\bar {k}})}$

${\displaystyle e_{i{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}-j-{\bar {j}}-k-{\bar {k}})}$

${\displaystyle e_{j{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}+j+{\bar) {j}}-k-{\bar {k}})}$

${\displaystyle e_{k{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}-j-{\ çubuk {j}}+k+{\bar {k}})}$

${\displaystyle e_{2}={\tfrac {2}{8}}(2e-2{\bar {e}})={\tfrac {1}{2}}(e-{\bar {e} })}$.

Bu indirgenemez ideallerin her biri gerçek bir merkezi basit cebire eşbiçimlidir , ilk dördü gerçek alana göredir . Geçen İdeal izomorftur çarpık alanın içinde kuaterniyonlara yazışma yoluyla:${\displaystyle \mathbb {R} }$${\ Displaystyle (e_{2})}$ ${\displaystyle \mathbb {H} }$

${\displaystyle \textstyle {\frac {1}{2}}(e-{\bar {e}})\longleftrightarrow 1,\ \ {\frac {1}{2}}(i-{\bar {i }})\longleftrightarrow i,\ \ {\frac {1}{2}}(j-{\bar {j}})\longleftrightarrow j,\ \ {\frac {1}{2}}(k-{ \bar {k}})\longleftrightarrow k.}$

Ayrıca, tarafından verilen projeksiyon homomorfizmi , idempotent tarafından üretilen çekirdek idealine sahiptir:${\displaystyle \mathbb {R} [Q_{8}]\to (e_{2})\cong \mathbb {H} }$${\displaystyle r\mapsto yeniden_{2}}$

${\displaystyle e_{2}^{\perp }\ =\ \textstyle e_{1}+e_{i{\text{-ker}}}+e_{j{\text{-ker}}}+e_{ k{\text{-ker}}}\ =\ {\frac {1}{2}}(e+{\bar {e}}),}$

böylece kuaterniyonlar bölüm halkası olarak da elde edilebilir . ${\displaystyle \mathbb {R} [Q_{8}]/(e+{\bar {e}})\cong \mathbb {H} }$

Karmaşık grup cebiri böylece , biquaternionların cebiri nerede . ${\displaystyle \mathbb {C} [Q_{8}]\cong \mathbb {C} ^{\oplus 4}\oplus M_{2}(\mathbb {C} )}$${\displaystyle M_{2}(\mathbb {C} )\cong \mathbb {H} \otimes _{\mathbb {R} }\!\mathbb {C} \cong \mathbb {H} \oplus \mathbb { H} }$

matris temsilleri

SL'nin bir alt grubu olarak kuaterniyon grubunun çarpım tablosu (2, C ). Girişler, argümanlarına karşılık gelen sektörlerle temsil edilir: 1 (yeşil), i (mavi), -1 (kırmızı), - i (sarı).

İki boyutlu indirgenemez kompleks gösterimi , yukarıda tarif edilen Dördey Q grubunu veren ₈ bir alt grup olarak genel lineer grubu . Kuaterniyon grubu, dördey cebirinin , kendi üzerinde sol çarpma ile düzenli bir temsili olan, tabanlı karmaşık bir vektör uzayı olarak kabul edilen , dolayısıyla C- doğrusal eşlemeye karşılık gelen bir çarpımsal alt grubudur . Ortaya çıkan temsil şu şekilde verilir: ${\displaystyle \operatöradı {GL} (2,\mathbb {C} )}$${\displaystyle \mathbb {H} =\mathbb {R} 1+\mathbb {R} i+\mathbb {R} j+\mathbb {R} k=\mathbb {C} 1+\mathbb {C} j}$ ${\displaystyle \rho :\mathbb {H} \to \mathrm {M} _{2}(\mathbb {C} )}$${\görüntüleme stili \{1,j\}}$${\displaystyle z\in \mathbb {H} }$${\displaystyle \rho _{z}:a{+}jb\mapsto z\cdot (a{+}jb)}$${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {GL} (2,\mathbb {C} ),\ g\mapsto \rho _{g},}$

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&\!\!\!\!- i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&\!\!\!\!-1\\1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\! \!\!-i\\\!\!\!-i&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0& \!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-i&0\\0&i\end{pmatrix}}& {\overline {j}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&i\ \i&0\end{pmatrix}}.\end{matris}}}$

Yukarıdaki matrislerin tüm birim belirleyici olduğundan, bu Q bir temsilidir ₈ içinde özel lineer grubu SL (2, Cı- ).

Bir varyant, üniter matrislerle bir temsil verir (sağdaki tablo). Doğrusal eşlemeye karşılık gelelim , böylece şu şekilde verilir: ${\displaystyle g\in Q_{8}}$${\displaystyle \rho _{g}:a{+}bj\mapsto (a{+}bj)\cdot jg^{-1}j^{-1}}$${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {SU} (2)}$

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&\!\!\!\!- i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix }}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-i&0\\0&i\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}0&\!\! \!\!-1\\1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&\!\!\!\!-i\\\!\!\! -i&0\end{pmatrix}}.\end{matris}}}$

Fizikçilerin , alışılmış Pauli matrisleriyle bağlantı kurmak için matris temsili için yalnızca farklı bir kural kullandıklarını belirtmekte fayda var : ${\ Displaystyle \ matematik {SU} (2)}$

${\displaystyle {\begin{matrix}&e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}=\quad \,1_{2\times 2}&i\mapsto {\begin{pmatrix}0& \!\!\!-i\!\\\!\!-i\!\!&0\end{pmatrix}}=-i\sigma _{x}&j\mapsto {\başlangıç{pmatrix}0&\! \!\!-1\!\\1&0\end{pmatrix}}=-i\sigma _{y}&k\mapsto {\begin{pmatrix}\!\!-i\!\!&0\\0&i\ end{pmatrix}}=-i\sigma _{z}\\&{\overline {e}}\mapsto {\begin{pmatrix}\!\!-1\!&0\\0&\!\!\! -1\!\end{pmatrix}}=-1_{2\times 2}&{\overline {i}}\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}=\,\, \,\,i\sigma _{x}&{\overline {j}}\mapsto {\begin{pmatrix}0&1\\\!\!-1\!\!&0\end{pmatrix}}=\, \,\,\,i\sigma _{y}&{\overline {k}}\mapsto {\begin{pmatrix}i&0\\0&\!\!\!-i\!\end{pmatrix}}= \,\,\,\,i\sigma _{z}.\end{matris}}}$

Tek açıklanır, bu belirli bir seçim kullanışlı ve zarif Spin-1/2 devletleri içinde bazda dikkate açısal momentum merdiven operatörlerini . ${\displaystyle ({\vec {J}}^{2},J_{z})}$ ${\displaystyle J_{\pm }=J_{x}\pm iJ_{y}}$

SL(2,3)' ün bir alt grubu olarak dördey grubunun çarpım tablosu . Alan öğeleri 0,+,− ile gösterilir.

Ayrıca, F ₃ = {0,1,−1} (sağdaki tablo) sonlu alanı üzerinde 2 boyutlu vektör uzayı üzerinde Q _8'in önemli bir etkisi vardır . Bir modüler gösterimi ile verilir ${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {SL} (2,3)}$

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}1&1\\1&\!\!\!\!- 1\end{pmatrix}}&j\mapsto {\begin{pmatrix}\!\!\!-1&1\\1&1\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\!\!\ !-1\\1&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1 \end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-1&\!\!\!\!-1\\\!\!\!-1&1 \end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}1&\!\!\!\!-1\\\!\!\!-1&\!\!\!\ !-1\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}.\end{matrix}}}$

Bu gösterim, F ₉ = F ₃ [ k ] = F ₃ 1 + F ₃ k uzantı alanından elde edilebilir , burada k ² = -1 ve çarpımsal grup ( F ₉ ) ^× , jeneratörlere sahiptir ±( k +1), (± k -1) için 8. iki boyutlu F ₃ -vector alanı F ₉ doğrusal eşlemeler kabul için z olarak F ₉ , hem de Frobemino otomorfizm tatmin edici ve . O zaman yukarıdaki temsil matrisleri , , , ve . ${\displaystyle \mu _{z}(a+bk)=z\cdot (a+bk)}$ ${\displaystyle \phi (a+bk)=(a+bk)^{3}}$${\displaystyle \phi ^{2}=\mu _{1}}$${\displaystyle \phi \mu _{z}=\mu _{\phi (z)}\phi }$${\displaystyle \rho ({\bar {e}})=\mu _{-1}}$${\displaystyle \rho (i)=\mu _{k+1}\phi }$${\displaystyle \rho (j)=\mu _{k-1}\phi }$${\displaystyle \rho (k)=\mu _{k}}$

Yukarıdaki temsili Q fark ₈ bir şekilde normal bir alt-grubu içinde GL (2, 3) . Böylece, her matris için , ile tanımlanan bir grup otomorfizmasına sahibiz . Aslında, bunlar tam otomorfizm grubunu şu şekilde verir: ${\displaystyle m\in \mathrm {GL} (2,3)}$${\displaystyle \psi _{m}:Q_{8}\to Q_{8}}$${\displaystyle \psi _{m}(g)=mgm^{-1}}$${\displaystyle \psi _{I}=\psi _{-I}=\mathrm {id} _{Q_{8}}}$

${\displaystyle \mathrm {Aut} (Q_{8})\cong \mathrm {PGL} (2,3)=\mathrm {GL} (2,3)/\{\pm I\}\cong S_{4 }}$,

Bu simetrik grup S izomorf ₄ lineer dönüşümler yana permute dört tek boyutlu alt uzay , yani dört nokta yansıtmalı alanı . ${\displaystyle m:\mathbb {F} _{3}^{2}\to \mathbb {F} _{3}^{2}}$${\displaystyle \mathbb {F} _{3}^{2}}$ ${\displaystyle \mathbb {P} _{\mathbb {F} _{3}}^{1}=\mathrm {PG} (1,3)}$

Aynı zamanda, bu gösterim permütasyona sekiz sıfır olmayan vektörleri ( F ₃ ) ² ve Q nun, bir gömme veren ₈ içinde simetrik grubunun S _{, 8} normal temsillerin verilen tespitlerinin ilave olarak.

Galois grubu

Richard Dean'in 1981'de gösterdiği gibi, kuaterniyon grubu Galois grubu Gal(T/ Q ) olarak sunulabilir; burada Q , rasyonel sayıların alanıdır ve T, polinomun Q üzerindeki bölme alanıdır .

${\displaystyle x^{8}-72x^{6}+180x^{4}-144x^{2}+36}$.

Geliştirme , Galois teorisinin temel teoremini, Q ve T ve bunların Galois grupları arasındaki dört ara alanı ve ayrıca bir alan üzerinde dördüncü derecenin döngüsel genişlemesine ilişkin iki teoremi belirtirken kullanır.

Genelleştirilmiş kuaterniyon grubu

Bir genelleştirilmiş kuaternion grubu Q _{4 , n} için 4 N sunumu ile tanımlanır

${\displaystyle \langle x,y\mid x^{2n}=y^{4}=1,x^{n}=y^{2},y^{-1}xy=x^{-1} \ menzil }$

bir tamsayı için n ≥ 2 tarafından verilen olağan Dördey grubu ile, n = 2 Coxeter Q aramaları _{4 N} disiklik grubu , özel bir durumunda , ikili çok yüzlü grubu ve ilişkin bir çok-yüzlü grubu ve dihedral grubu . Genelleştirilmiş kuaterniyon grubu, tarafından oluşturulan alt grubu olarak gerçekleştirilebilir . ${\displaystyle \langle 2,2,n\rangle }$ ${\displaystyle \langle \ell ,m,n\rangle }$ ${\görüntüleme stili (p,q,r)}$ ${\görüntüleme stili (2,2,n)}$${\displaystyle \operatöradı {GL} _{2}(\mathbb {C} )}$

${\displaystyle \left({\begin{array}{cc}\omega _{n}&0\\0&{\overline {\omega }}_{n}\end{array}}\right){\mbox{ ve }}\left({\başlangıç{dizi}{cc}0&-1\\1&0\end{dizi}}\sağ)}$

nerede . Ayrıca ve tarafından üretilen birim kuaterniyonların alt grubu olarak da gerçekleştirilebilir . ${\displaystyle \omega _{n}=e^{i\pi /n}}$${\displaystyle x=e^{i\pi /n}}$${\görüntüleme stili y=j}$

Genelleştirilmiş kuaterniyon grupları, her değişmeli alt grubun döngüsel olma özelliğine sahiptir . Bu özelliğe sahip bir sonlu p - grubunun (her değişmeli alt grup döngüseldir) yukarıda tanımlandığı gibi ya döngüsel ya da genelleştirilmiş bir kuaterniyon grubu olduğu gösterilebilir. Başka bir karakterizasyon sonlu olmasıdır p -grubu sırası eşsiz bir alt grubu vardır p ya siklik ya da genel Dördey grubu izomorf 2 grubudur. Özellikle, tek karakteristikli sonlu bir F alanı için , SL _2'nin ( F ) 2-Sylow alt grubu değişmeli değildir ve 2. dereceden yalnızca bir alt gruba sahiptir, bu nedenle bu 2-Sylow alt grubu genelleştirilmiş bir kuaterniyon grubu olmalıdır, ( Gorenstein 1980 , s. 42). İzin vermek p ^r büyüklüğünde olabilir F , s asal, SL 2-Sylow alt grup büyüklüğü ₂ ( F ) 2 ^{, n} , burada n = Ord ₂ ( p ² - 1) + Ord ₂ ( R ) .

Brauer Suzuki teoremi gösterir olan Sylow 2-alt gruplar genelleştirilmiştir Dördey grupları basit olamaz.

Başka bir terminoloji, sunumu kabul eden 2'lik bir dereceli disiklik bir grup için "genelleştirilmiş kuaterniyon grubu" adını saklı tutar.

${\displaystyle \langle x,y\mid x^{2^{m}}=y^{4}=1,x^{2^{m-1}}=y^{2},y^{- 1}xy=x^{-1}\rangle .}$

Ayrıca bakınız

• 16 hücreli
• İkili tetrahedral grup
• Clifford cebiri
• disiklik grup
• Hurwitz integral dördey
• Küçük grupların listesi

Notlar

Referanslar

• Artin, Michael (1991), Cebir , Prentice Hall, ISBN 978-0-13-004763-2
• Brown, Kenneth S. (1982), Grupların Kohomolojisi (3. baskı), Springer-Verlag, ISBN 978-0-387-90688-1
• Cartan, Henri ; Eilenberg, Samuel (1999), Homolojik Cebir , Princeton University Press, ISBN 978-0-691-04991-5
• Coxeter, HSM & Moser, WOJ (1980). Ayrık Gruplar için Üreticiler ve İlişkiler . New York: Springer-Verlag. ISBN'si 0-387-09212-9.
• Dean, Richard A. (1981) "Grubu kuaterniyonlar olan bir rasyonel polinom", American Mathematical Monthly 88:42–5.
• Gorenstein, D. (1980), Sonlu Gruplar , New York: Chelsea, ISBN 978-0-8284-0301-6, MR  0569209
• Johnson, David L. (1980), Grup sunumları teorisindeki konular , Cambridge University Press , ISBN 978-0-521-23108-4, MR  0695161
• Rotman, Joseph J. (1995), Gruplar teorisine giriş (4. baskı), Springer-Verlag, ISBN 978-0-387-94285-8
• PR Girard (1984) "Dördey grubu ve modern fizik", European Journal of Physics 5:25–32.
• Hall, Marshall (1999), Grup teorisi (2. baskı), AMS Kitabevi, ISBN 0-8218-1967-4
• Kurosh, Alexander G. (1979), Gruplar Teorisi , AMS Kitabevi, ISBN 0-8284-0107-1

Dış bağlantılar

• Weisstein, Eric W. "Dörtlü grup" . Matematik Dünyası .
• Grup Adlarında Kuaternion grupları
• GroupProps'ta Kuaternion grubu
• Conrad, Keith. "Genelleştirilmiş Kuaterniyonlar"