Lojistik regresyon - Logistic regression

Gelen istatistik , lojistik modeli (veya logit modeli ) mevcut belirli bir sınıfın olasılığını veya olayı modellemek için kullanılan gibi pas / / kaybetseydi, / diri ölü veya sağlıklı / hastaları kazanmak, başarısız. Bu, bir görüntünün kedi, köpek, aslan vb. içerip içermediğini belirlemek gibi çeşitli olay sınıflarını modellemek için genişletilebilir. Görüntüde algılanan her nesneye, toplamı bir olmak üzere 0 ile 1 arasında bir olasılık atanacaktır.

Lojistik regresyon, daha birçok karmaşık uzantı olmasına rağmen , temel biçiminde ikili bağımlı değişkeni modellemek için bir lojistik işlevi kullanan istatistiksel bir modeldir . Olarak regresyon analizi , lojistik regresyon (veya logit geri çekilme ) olduğu tahmin lojistik modeli (bir çeşit parametrelerini ikili regresyon ). Matematiksel olarak, bir ikili lojistik model, iki değerin "0" ve "1" olarak etiketlendiği bir gösterge değişkeni tarafından temsil edilen başarılı/başarısız gibi iki olası değere sahip bir bağımlı değişkene sahiptir . Lojistik modelde, log-olasılık ( logaritma arasında oran "1" etiketli değeri için) olan lineer bir kombinasyonu , bir ya da daha fazla bağımsız değişkenler ( "belirleyicileri"); bağımsız değişkenlerin her biri bir ikili değişken (bir gösterge değişkeni tarafından kodlanmış iki sınıf) veya bir sürekli değişken (herhangi bir gerçek değer) olabilir. "1" etiketli değerin karşılık gelen olasılığı 0 (kesinlikle "0" değeri) ile 1 (kesinlikle "1" değeri) arasında değişebilir, dolayısıyla etiketleme; log-oranları olasılığa çeviren fonksiyon lojistik fonksiyondur, dolayısıyla adıdır. Ölçüm birimi log-olasılık ölçek için bir adlandırılır logit gelen günlük istik un buna , dolayısıyla alternatif isimler. Probit modeli gibi lojistik fonksiyon yerine farklı bir sigmoid fonksiyonuna sahip benzer modeller de kullanılabilir ; lojistik modelin tanımlayıcı özelliği, bağımsız değişkenlerden birinin artırılmasının, verilen sonucun olasılıklarını, her bağımsız değişkenin kendi parametresine sahip olduğu sabit bir oranda çarpımsal olarak ölçeklendirmesidir ; bir ikili bağımlı değişken için bu, olasılık oranını genelleştirir .

İkili lojistik regresyon modelinde, bağımlı değişkenin iki düzeyi vardır ( kategorik ). İkiden çok değeri olan çıkışlar tarafından modellenir çokterimli lojistik regresyon birden kategoriler halinde ve sıralı olarak, sıralı lojistik regresyon (örneğin orantılı oranları lojistik model Sıra). Lojistik regresyon modeli, çıktının olasılığını girdi açısından basitçe modeller ve istatistiksel sınıflandırma yapmaz (bir sınıflandırıcı değildir), ancak örneğin bir kesme değeri seçerek ve girdileri olasılık ile sınıflandırarak bir sınıflandırıcı yapmak için kullanılabilir. bir sınıf olarak sınır değerden büyük, diğeri olarak sınır değerin altında; bu, ikili bir sınıflandırıcı yapmanın yaygın bir yoludur . Katsayılar, doğrusal en küçük karelerin aksine, genellikle kapalı biçimli bir ifadeyle hesaplanmaz ; bkz. § Model uydurma . Genel bir istatistiksel model olarak lojistik regresyon, ilk olarak Joseph Berkson tarafından geliştirildi ve popülerleştirildi , Berkson'dan (1944) başlayarak "logit"i icat etti; bkz. § Geçmiş . harvtxt hatası: hedef yok: CITEREFBerkson1944 ( yardım )

Bir serinin parçası
Regresyon analizi
Modeller
Doğrusal regresyon Basit regresyon polinom regresyon Genel doğrusal model
Genelleştirilmiş doğrusal model ayrık seçim Binom regresyon ikili regresyon Lojistik regresyon Çok terimli lojistik regresyon karışık logit yasaklamak çok terimli probit sıralı logit sıralı probit zehir
çok seviyeli model Sabit efektler rastgele efektler Doğrusal karışık efekt modeli Doğrusal olmayan karışık efekt modeli
Doğrusal olmayan regresyon Parametrik olmayan yarı parametrik güçlü Çeyreklik izotonik Ana bileşenleri En küçük açı Yerel bölümlere ayrılmış
Değişkenlerdeki hatalar
Tahmin
En küçük kareler Doğrusal doğrusal olmayan
Sıradan Ağırlıklı genelleştirilmiş
Kısmi Toplam Negatif olmayan sırt regresyonu düzenli
En küçük mutlak sapmalar yinelemeli olarak yeniden ağırlıklandırılmış Bayes Bayes çok değişkenli
Arka plan
Regresyon doğrulama Ortalama ve tahmin edilen yanıt Hatalar ve artıklar Formda olmanın güzelliği Öğrencileştirilmiş kalıntı Gauss-Markov teoremi
matematik portalı
v T e

Uygulamalar

Lojistik regresyon, makine öğrenimi, çoğu tıp alanı ve sosyal bilimler dahil olmak üzere çeşitli alanlarda kullanılmaktadır. Örneğin, yaralı hastalarda mortaliteyi tahmin etmek için yaygın olarak kullanılan Travma ve Yaralanma Şiddet Skoru ( TRISS ), orijinal olarak Boyd ve ark. lojistik regresyon kullanılarak Bir hastanın şiddetini değerlendirmek için kullanılan diğer birçok tıbbi ölçek, lojistik regresyon kullanılarak geliştirilmiştir. Lojistik regresyon , hastanın gözlenen özelliklerine (yaş, cinsiyet, vücut kitle indeksi , çeşitli kan testlerinin sonuçları , vb.) dayalı olarak belirli bir hastalığın (örneğin diyabet ; koroner kalp hastalığı ) gelişme riskini tahmin etmek için kullanılabilir . Başka bir örnek, Nepalli bir seçmenin yaş, gelir, cinsiyet, ırk, ikamet durumu, önceki seçimlerdeki oylar vb. temelinde Nepal Kongresi'ne veya Nepal Komünist Partisi'ne veya Herhangi Bir Diğer Partiye oy verip vermeyeceğini tahmin etmek olabilir. mühendislikte , özellikle belirli bir süreç, sistem veya ürünün arıza olasılığını tahmin etmek için kullanılır . Ayrıca, bir müşterinin bir ürünü satın alma veya aboneliği durdurma eğiliminin tahmini gibi pazarlama uygulamalarında da kullanılır. Ekonomide , bir kişinin işgücüne katılma olasılığını tahmin etmek için kullanılabilir ve bir iş uygulaması, bir ev sahibinin ipoteği temerrüde düşürme olasılığını tahmin etmektir . Sıralı verilere lojistik regresyonun bir uzantısı olan koşullu rastgele alanlar , doğal dil işlemede kullanılır .

Örnekler

lojistik model

Verilen parametrelere sahip bir lojistik modeli göz önünde bulundurarak lojistik regresyonu anlamaya çalışalım, ardından katsayıların verilerden nasıl tahmin edilebileceğini görelim. İki yordayıcılı bir model düşünün ve , ve bir ikili (Bernoulli) yanıt değişkeni ile ifade edelim . Tahmin değişkenleri ile olayın log-oranları (logit olarak da adlandırılır) arasında doğrusal bir ilişki olduğunu varsayıyoruz . Bu doğrusal ilişki aşağıdaki matematiksel biçimde yazılabilir (burada ℓ log-orandır, logaritmanın temelidir ve modelin parametreleridir): ${\görüntüleme stili x_{1}}$${\displaystyle x_{2}}$${\görüntüleme stili Y}$${\görüntüleme stili p=P(Y=1)}$${\görüntüleme stili Y=1}$${\görüntüleme stili b}$${\ Displaystyle \ beta _ {i}}$

${\displaystyle \ell =\log _{b}{\frac {p}{1-p}}=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_ {2}}$

Log oranlarını katlayarak oranları kurtarabiliriz :

${\displaystyle {\frac {p}{1-p}}=b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}$.

Basit cebir manipülasyon edebilen (yer tarafından pay ve payda bölerek ), olasılık olduğu ${\displaystyle b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}$${\görüntüleme stili Y=1}$

${\displaystyle p={\frac {b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}{b^{\beta _{ 0}+\beta _{1}x_{1}+\beta _{2}x_{2}}+1}}={\frac {1}{1+b^{-(\beta _{0} +\beta _{1}x_{1}+\beta _{2}x_{2})}}}=S_{b}(\beta _{0}+\beta _{1}x_{1}+ \beta _{2}x_{2})}$.

Burada bir sigmoid fonksiyonu baz ile . Yukarıdaki formül, bir kez sabitlendiğinde, belirli bir gözlem için log-oranları veya belirli bir gözlem için olasılığı kolayca hesaplayabileceğimizi gösterir . Bir lojistik modeli, ana kullanım durum, bir gözlem verilecek olan ve olasılığına olduğu . Çoğu uygulamada, logaritmanın tabanı genellikle e olarak alınır . Bununla birlikte, bazı durumlarda, taban 2 veya taban 10'da çalışarak sonuçları iletmek daha kolay olabilir. ${\ Displaystyle S_{b}}$${\görüntüleme stili b}$${\ Displaystyle \ beta _ {i}}$${\görüntüleme stili Y=1}$${\görüntüleme stili Y=1}$${\displaystyle (x_{1},x_{2})}$${\görüntüleme stili p}$${\görüntüleme stili Y=1}$${\görüntüleme stili b}$

Biz içeren bir örnek ve katsayıları , ve . Somut olmak gerekirse, model ${\görüntüleme stili b=10}$${\displaystyle \beta _{0}=-3}$${\displaystyle \beta _{1}=1}$${\displaystyle \beta _{2}=2}$

${\displaystyle \log _{10}{\frac {p}{1-p}}=\ell =-3+x_{1}+2x_{2}}$

nerede o olayı olasılığıdır . ${\görüntüleme stili p}$${\görüntüleme stili Y=1}$

Bu şu şekilde yorumlanabilir:

• ${\displaystyle \beta _{0}=-3}$olduğu Y -intercept . Bu olayın log-olasılık olduğunu , ongorduruculeri . Üs alarak, olayın oranlarının 1'e 1000 veya . Benzer şekilde, olayın ne zaman olarak hesaplanabileceği olasılığı .${\görüntüleme stili Y=1}$${\displaystyle x_{1}=x_{2}=0}$${\displaystyle x_{1}=x_{2}=0}$${\görüntüleme stili Y=1}$${\görüntüleme stili 10^{-3}}$${\görüntüleme stili Y=1}$${\displaystyle x_{1}=x_{2}=0}$${\displaystyle 1/(1000+1)=1/1001}$
• ${\displaystyle \beta _{1}=1}$1 artırmanın log oranlarını artırdığı anlamına gelir . Yani 1 artarsa, bir faktör kadar artan oranlar . Not o olasılık arasında da artmıştır, ancak oran artmıştır gibi kadar artmadığını.${\görüntüleme stili x_{1}}$${\görüntüleme stili 1}$${\görüntüleme stili x_{1}}$${\görüntüleme stili Y=1}$${\görüntüleme stili 10^{1}}$${\görüntüleme stili Y=1}$
• ${\displaystyle \beta _{2}=2}$1 artırmanın log oranlarını artırdığı anlamına gelir . Dolayısıyla , 1 artarsa, bir faktör kadar artan oranlar Notun log-ordlar üzerindeki etkisinin, 'nin etkisinin iki katı , ancak oranlar üzerindeki etkisi 10 kat daha fazladır. Ama üzerindeki etki olasılığı arasında 10 kat daha fazladır oran üzerinde tek etkisi, değil 10 kadar kat daha fazladır.${\displaystyle x_{2}}$${\görüntüleme stili 2}$${\displaystyle x_{2}}$${\görüntüleme stili Y=1}$${\görüntüleme stili 10^{2}.}$${\displaystyle x_{2}}$${\görüntüleme stili x_{1}}$${\görüntüleme stili Y=1}$

Verilerden parametreleri tahmin etmek için lojistik regresyon yapılmalıdır. ${\ Displaystyle \ beta _ {i}}$

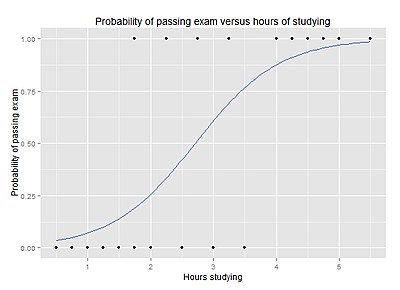
Bir sınavı geçme olasılığına karşı çalışma saatleri

Aşağıdaki soruyu cevaplamak için:

20 kişilik bir öğrenci grubu, bir sınava çalışmak için 0 ile 6 saat arasında zaman harcar. Ders çalışmak için harcanan saat, öğrencinin sınavı geçme olasılığını nasıl etkiler?

Bu problem için lojistik regresyon kullanılmasının nedeni, "1" ve "0" ile temsil edilen bağımlı değişken, başarılı ve başarısız değerlerinin kardinal sayılar olmamasıdır . Sorun başarılı/başarısız 0-100 (ana sayılar) notu ile değiştirilecek şekilde değiştirilirse, basit regresyon analizi kullanılabilir.

Tablo, her öğrencinin ders çalışmak için harcadığı saat sayısını ve başarılı (1) veya başarısız (0) olup olmadığını gösterir.

Saat	0,50	0.75	1.00	1.25	1.50	1.75	1.75	2.00	2.25	2.50	2.75	3.00	3.25	3.50	4.00	4.25	4.50	4.75	5.00	5.50
Geçmek	0	0	0	0	0	0	1	0	1	0	1	0	1	0	1	1	1	1	1	1

Grafik, verilere lojistik regresyon eğrisi yerleştirildiğinde, sınavı geçme olasılığına karşı çalışma saatlerinin sayısını gösterir.

Lojistik regresyon analizi aşağıdaki çıktıyı verir.

	katsayı	Std. Hata	z değeri	P değeri (Wald)
Tutmak	-4.0777	1.7610	-2.316	0.0206
Saat	1.5046	0.6287	2.393	0.0167

Çıktı, çalışma saatlerinin sınavı geçme olasılığı ile önemli ölçüde ilişkili olduğunu gösterir ( , Wald testi ). Çıktı ayrıca ve için katsayıları sağlar . Bu katsayılar, sınavı geçme olasılığını (olasılığını) tahmin etmek için lojistik regresyon denklemine girilir: ${\görüntüleme stili p=0.0167}$${\displaystyle {\text{Kesme}}=-4.0777}$${\displaystyle {\text{Saat}}=1.5046}$

${\displaystyle {\begin{aligned}{\text{Sınavı geçme günlük oranları}}&=1.5046\cdot {\text{Saat}}-4.0777=1.5046\cdot ({\text{Saat}}-2.71) \\{\text{Sınavı geçme olasılığı}}&=\exp \left(1.5046\cdot {\text{Saat}}-4.0777\sağ)=\exp \left(1.55046\cdot ({\text{Saat}) }-2.71)\sağ)\\{\text{Sınavı geçme olasılığı}}&={\frac {1}{1+\exp \left(-\left(1.55046\cdot {\text{Saat}})- 4.0777\sağ)\sağ)}}\end{hizalı}}}$

Çalışmanın ilave bir saat geçen oran çarpımı, yani 1.5046 geçirerek log-oranları artacağı tahmin edilmektedir ile biçiminde X -intercept (2.71) gösterir, bu tahminler daha oran (log-olasılık 0, oran 1, olasılık 1 (2) 2,71 saat okuyan bir öğrenci için. ${\displaystyle \exp(1.5046)\yaklaşık 4.5.}$

Örneğin, 2 saat çalışan bir öğrenci için denklemdeki değeri girmek , tahmini 0.26 sınavı geçme olasılığını verir: ${\displaystyle {\metin{Saat}}=2}$

${\displaystyle {\text{Sınavı geçme olasılığı}}={\frac {1}{1+\exp \left(-\left(1.55046\cdot 2-4.0777\right)\right)}}=0.26}$

Benzer şekilde, 4 saat çalışan bir öğrencinin sınavı geçme olasılığı tahmini 0.87'dir:

${\displaystyle {\text{Sınavı geçme olasılığı}}={\frac {1}{1+\exp \left(-\left(1.55046\cdot 4-4.0777\right)\right)}}=0.87}$

Bu tablo, çalışma saatlerinin birkaç değeri için sınavı geçme olasılığını gösterir.

çalışma saatleri	sınavı geçmek
	Günlük oranları	oranlar	olasılık
1	-2.57	0.076 = 1:13.1	0.07
2	-1.07	0.34 ≈ 1:2.91	0.26
3	0.44	1.55	0.61
4	1,94	6.96	0.87
5	3.45	31.4	0.97

Lojistik regresyon analizinden elde edilen çıktı , Wald z-skoruna dayanan bir p-değeri verir . Aksine Wald yöntemine göre, lojistik regresyon p-değerini hesaplamak için tavsiye edilen bir yöntemdir olabilirlik-oran testi (MDT), bu veriler için verir . ${\görüntüleme stili p=0.0167}$${\görüntüleme stili p=0.0006}$

Tartışma

Lojistik regresyon binom, sıralı veya çok terimli olabilir. Binom veya ikili lojistik regresyon, bağımlı bir değişken için gözlemlenen sonucun yalnızca iki olası türe, "0" ve "1"e sahip olabileceği durumlarla ilgilenir (örneğin, "geçti" ile "başarısız" veya "kazandı"yı temsil edebilir). " ve "kayıp"). Çok terimli lojistik regresyon , sonucun sıralanmamış üç veya daha fazla olası tipe (örneğin, "hastalık A" ve "hastalık B" ve "hastalık C") sahip olabileceği durumlarla ilgilenir. Sıralı lojistik regresyon , sıralı bağımlı değişkenlerle ilgilenir.

İkili lojistik regresyonda, sonuç genellikle "0" veya "1" olarak kodlanır, çünkü bu en basit yoruma yol açar. Bağımlı değişken için belirli bir gözlemlenen sonuç, dikkate değer olası sonuçsa ("başarı" veya "örnek" veya "durum" olarak adlandırılır) genellikle "1" olarak kodlanır ve bunun tersi sonuç (bir sonuç olarak adlandırılır) "hata" veya "olmayan" veya "olmayan") "0" olarak. İkili lojistik regresyon, bağımsız değişkenlerin (yordayıcıların) değerlerine dayalı bir durum olma olasılığını tahmin etmek için kullanılır . Oranlar, belirli bir sonucun bir vaka olma olasılığının, bunun bir durum olmama olasılığına bölümü olarak tanımlanır.

Diğer regresyon analizi biçimleri gibi , lojistik regresyon, sürekli veya kategorik olabilen bir veya daha fazla tahmin değişkenini kullanır. Bununla birlikte, sıradan lineer regresyondan farklı olarak, lojistik regresyon, sürekli bir sonuçtan ziyade sınırlı sayıda kategoriden birine üyelik alan bağımlı değişkenleri tahmin etmek için kullanılır (binom durumundaki bağımlı değişkeni bir Bernoulli denemesinin sonucu olarak ele alır). Bu fark göz önüne alındığında, doğrusal regresyon varsayımları ihlal edilir. Özellikle, artıklar normal dağılamaz. Ek olarak, doğrusal regresyon, ikili bağımlı değişken için anlamsız tahminler yapabilir. İhtiyaç duyulan şey, bir ikili değişkeni herhangi bir gerçek değeri (negatif veya pozitif) alabilen sürekli bir değişkene dönüştürmenin bir yoludur. Bunu yapmak için, binom lojistik regresyon önce her bağımsız değişkenin farklı seviyeleri için olayın olma ihtimalini hesaplar ve ardından bağımlı değişkenin dönüştürülmüş bir versiyonu olarak sürekli bir kriter oluşturmak için logaritmasını alır . Oran logaritmasıdır logit , olasılık logit şu şekilde tanımlanır:

${\displaystyle \operatorname {logit} p=\ln {\frac {p}{1-p}}\quad {\text{için }}0<p<1\,.}$

Lojistik regresyonda bağımlı değişken Bernoulli olmasına rağmen, logit sınırsız bir ölçektedir. Logit işlevi, bu tür genelleştirilmiş doğrusal modeldeki bağlantı işlevidir , yani

${\displaystyle \operatöradı {logit} \operatöradı {\mathcal {E}} (Y)=\beta _{0}+\beta _{1}x}$

Y , Bernoulli tarafından dağıtılan yanıt değişkenidir ve x , öngörücü değişkendir; β değerleri doğrusal parametrelerdir.

Logit başarı olasılığı daha sonra tahmincileri ile donatılmıştır. Logitin tahmin edilen değeri , doğal logaritmanın tersi olan üstel fonksiyon aracılığıyla tekrar tahmin edilen oranlara dönüştürülür . Dolayısıyla, ikili lojistik regresyonda gözlenen bağımlı değişken 0 veya 1 değişken olmasına rağmen, lojistik regresyon, bağımlı değişkenin bir 'başarı' olma ihtimalini sürekli bir değişken olarak tahmin eder. Bazı uygulamalarda, ihtiyaç duyulan tek şey oranlardır. Diğerlerinde, bağımlı değişkenin bir 'başarı' olup olmadığı konusunda özel bir evet-hayır tahmini gereklidir; bu kategorik tahmin, hesaplanan başarı oranlarına dayanabilir, seçilen bazı kesme değerlerinin üzerindeki tahmin edilen oranlar, bir başarı tahminine dönüştürülür.

Doğrusal tahmin etkileri varsayımı, spline fonksiyonları gibi teknikler kullanılarak kolaylıkla gevşetilebilir .

Lojistik regresyon ve diğer yaklaşımlar

Lojistik regresyon , lojistik dağılımın kümülatif dağılım işlevi olan bir lojistik işlevi kullanarak olasılıkları tahmin ederek kategorik bağımlı değişken ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi ölçer . Bu nedenle, aynı problem setini benzer teknikler kullanarak probit regresyonu olarak ele alır, ikincisi bunun yerine kümülatif bir normal dağılım eğrisi kullanır. Eşdeğer olarak, bu iki yöntemin gizli değişken yorumlarında, birincisi standart bir lojistik hata dağılımını , ikincisi ise standart bir normal hata dağılımını varsayar .

Lojistik regresyon, genelleştirilmiş lineer modelin özel bir durumu olarak görülebilir ve dolayısıyla lineer regresyona benzer . Bununla birlikte, lojistik regresyon modeli, lineer regresyondan oldukça farklı varsayımlara (bağımlı ve bağımsız değişkenler arasındaki ilişki hakkında) dayanmaktadır. Özellikle, bu iki model arasındaki temel farklar, lojistik regresyonun aşağıdaki iki özelliğinde görülebilir. İlk olarak, koşullu dağılım bir Gauss dağılımından ziyade bir Bernoulli dağılımıdır , çünkü bağımlı değişken ikilidir. İkincisi, tahmin edilen değerler olasılıklardır ve bu nedenle lojistik dağıtım fonksiyonu aracılığıyla (0,1) ile sınırlandırılır çünkü lojistik regresyon , sonuçların kendisinden ziyade belirli sonuçların olasılığını tahmin eder . ${\görüntüleme stili y\orta x}$

Lojistik regresyon, Fisher'in 1936 yöntemi olan lineer diskriminant analizine bir alternatiftir . Doğrusal diskriminant analizinin varsayımları geçerliyse, lojistik regresyon üretmek için koşullandırma tersine çevrilebilir. Ancak bunun tersi doğru değildir, çünkü lojistik regresyon, diskriminant analizinin çok değişkenli normal varsayımını gerektirmez.

Gizli değişken yorumlama

Lojistik regresyon, basitçe en uygun parametreleri bulmak olarak anlaşılabilir : ${\görüntüleme stili \beta }$

${\displaystyle y={\begin{cases}1&\beta _{0}+\beta _{1}x+\varepsilon >0\\0&{\text{else}}\end{cases}}}$

standart lojistik dağıtım tarafından dağıtılan bir hata nerede . (Bunun yerine standart normal dağılım kullanılırsa, bu bir probit modelidir .) ${\görüntüleme stili\varepsilon }$

İlişkili gizli değişken . Hata terimi gözlendi ve bu nedenle değildir , aynı zamanda, gözlemlenemeyen, dolayısıyla "gizli" olarak adlandırılan (gözlemlenmiş değerleridir ve ). Bununla birlikte, sıradan regresyondan farklı olarak, parametreler , gözlemlenen verilerdeki ve değerlerinin herhangi bir doğrudan formülü ile ifade edilemez . Bunun yerine, genellikle bir yazılım programı tarafından uygulanan, tüm gözlenen ve değerlerin bir fonksiyonu olan karmaşık bir "olasılık ifadesinin" maksimumunu bulan yinelemeli bir arama süreciyle bulunurlar . Tahmin yaklaşımı aşağıda açıklanmıştır. ${\displaystyle y'=\beta _{0}+\beta _{1}x+\varepsilon }$${\görüntüleme stili\varepsilon }$${\görüntüleme stili y'}$${\görüntüleme stili y}$${\görüntüleme stili x}$${\görüntüleme stili \beta }$${\görüntüleme stili y}$${\görüntüleme stili x}$${\görüntüleme stili y}$${\görüntüleme stili x}$

Lojistik fonksiyon, oranlar, oranlar ve logit

Lojistik fonksiyonun tanımı

Lojistik regresyonun açıklaması, standart lojistik fonksiyonun açıklamasıyla başlayabilir . Lojistik işlevi, herhangi bir gerçek girdi alan ve sıfır ile bir arasında bir değer veren bir sigmoid işlevidir . Logit için bu, giriş log oranlarını almak ve çıkış olasılığına sahip olmak olarak yorumlanır . Standart lojistik fonksiyonu şu şekilde tanımlanır: ${\görüntüleme stili t}$${\displaystyle \sigma :\mathbb {R} \rightarrow (0,1)}$

${\displaystyle \sigma (t)={\frac {e^{t}}{e^{t}+1}}={\frac {1}{1+e^{-t}}}}$

Lojistik fonksiyonun t -aralığındaki (−6,6) grafiği Şekil 1'de gösterilmektedir.

Bize Varsayalım ki , tek bir doğrusal fonksiyonudur açıklayıcı değişken (bu durumda a, doğrusal bir kombinasyonudur ve benzer şekilde muamele edilir birden açıklayıcı değişkenlerin). O zaman aşağıdaki gibi ifade edebiliriz : ${\görüntüleme stili t}$ ${\görüntüleme stili x}$${\görüntüleme stili t}$${\görüntüleme stili t}$

${\displaystyle t=\beta _{0}+\beta _{1}x}$

Ve genel lojistik fonksiyon şimdi şu şekilde yazılabilir: ${\displaystyle p:\mathbb {R} \rightarrow (0,1)}$

${\displaystyle p(x)=\sigma (t)={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x)}}}}$

Lojistik modelde, bağımlı değişkenin başarısızlık/durum değil yerine başarı/vakaya eşit olma olasılığı olarak yorumlanır . Yanıt değişkenlerinin aynı şekilde dağıtılmadığı açıktır : bağımsız olarak verilen tasarım matrisi ve paylaşılan parametreler olmalarına rağmen bir veri noktasından diğerine farklılık gösterir . ${\görüntüleme stili p(x)}$${\görüntüleme stili Y}$ ${\görüntüleme stili Y_{i}}$${\displaystyle P(Y_{i}=1\orta X)}$${\displaystyle X_{i}}$ ${\görüntüleme stili X}$${\görüntüleme stili \beta }$

Lojistik fonksiyonun tersinin tanımı

Artık logit (log oranları) fonksiyonunu standart lojistik fonksiyonun tersi olarak tanımlayabiliriz . Şunları tatmin ettiğini görmek kolaydır: ${\displaystyle g=\sigma ^{-1}}$

${\displaystyle g(p(x))=\sigma ^{-1}(p(x))=\operatöradı {logit} p(x)=\ln \left({\frac {p(x)}} 1-p(x)}}\sağ)=\beta _{0}+\beta _{1}x,}$

ve eşdeğer olarak, her iki tarafı da üslendikten sonra şu olasılıklara sahibiz:

${\displaystyle {\frac {p(x)}{1-p(x)}}=e^{\beta _{0}+\beta _{1}x}.}$

Bu terimlerin yorumlanması

Yukarıdaki denklemlerde terimler aşağıdaki gibidir:

• ${\görüntüleme stili g}$logit fonksiyonudur. Denklem , logitin (yani, log-oranların veya oranların doğal logaritmasının) lineer regresyon ifadesine eşdeğer olduğunu gösterir.${\görüntüleme stili g(p(x))}$
• ${\görüntüleme stili \ln }$doğal logaritmayı ifade eder .
• ${\görüntüleme stili p(x)}$tahmin edicilerin bazı doğrusal kombinasyonları verildiğinde, bağımlı değişkenin bir duruma eşit olma olasılığıdır. Formül , bağımlı değişkenin bir duruma eşit olma olasılığının, doğrusal regresyon ifadesinin lojistik fonksiyonunun değerine eşit olduğunu gösterir. Bu, doğrusal regresyon ifadesinin değerinin negatiften pozitif sonsuza değişebileceğini ve yine de dönüşümden sonra olasılık için elde edilen ifadenin 0 ile 1 arasında değiştiğini göstermesi açısından önemlidir .${\görüntüleme stili p(x)}$${\görüntüleme stili p(x)}$
• ${\görüntüleme stili \beta _{0}}$olan kesişim (belirleyicisi sıfıra eşit olduğu zaman kriter değeri), lineer regresyon denkleminden.
• ${\displaystyle \beta _{1}x}$ tahmin edicinin bir değeri ile çarpılan regresyon katsayısıdır.
• taban , üstel işlevi belirtir.${\görüntüleme stili e}$

oranların tanımı

Bir duruma eşit olan bağımlı değişkenin olasılığı ( belirleyicilerin bazı doğrusal kombinasyonları verilir ), doğrusal regresyon ifadesinin üstel işlevine eşdeğerdir. Bu, logitin olasılık ve lineer regresyon ifadesi arasında nasıl bir bağlantı fonksiyonu olarak hizmet ettiğini gösterir . Logitin negatif ve pozitif sonsuz arasında değiştiği göz önüne alındığında, lineer regresyon yapmak için yeterli bir kriter sağlar ve logit kolayca tekrar oranlara dönüştürülür. ${\görüntüleme stili x}$

Bu nedenle, bir duruma eşit olan bağımlı değişkenin oranlarını ( tahmin edicilerin bazı doğrusal kombinasyonları göz önüne alındığında ) aşağıdaki gibi tanımlarız: ${\görüntüleme stili x}$

${\displaystyle {\text{odds}}=e^{\beta _{0}+\beta _{1}x}.}$

olasılık oranı

Sürekli bir bağımsız değişken için olasılık oranı şu şekilde tanımlanabilir:

${\displaystyle \mathrm {OR} ={\frac {\operatöradı {oranlar} (x+1)}{\operatöradı {odds} (x)}}={\frac {\left({\frac {p(x)) +1)}{1-p(x+1)}}\sağ)}{\sol({\frac {p(x)}{1-p(x)}}\sağ)}}={\frac {e^{\beta _{0}+\beta _{1}(x+1)}}{e^{\beta _{0}+\beta _{1}x}}}=e^{\ beta _{1}}}$

Bu üstel ilişki aşağıdakiler için bir yorum sağlar : x'teki her 1 birimlik artış için oranlar çarpılır . ${\görüntüleme stili \beta _{1}}$${\displaystyle e^{\beta _{1}}}$

İkili bağımsız bir değişken için olasılık oranı olarak tanımlanır burada bir , b , c ve d , 2 × 2 hücrelerdir durum tablo . ${\displaystyle {\frac {ad}{bc}}}$

Çoklu açıklayıcı değişkenler

Birden fazla açıklayıcı değişken varsa, yukarıdaki ifade şu şekilde revize edilebilir . Bu belirleyicileri değerlerine bir başarı günlük oranları bulunan denklem kullanılır O zaman, lineer regresyon bir olacaktır çoklu regresyon ile m explanators; tüm j = 0, 1, 2, ..., m parametrelerinin tümü tahmin edilir. ${\displaystyle \beta _{0}+\beta _{1}x}$${\displaystyle \beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m}=\beta _{ 0}+\sum _{i=1}^{m}\beta _{i}x_{i}}$${\görüntüleme stili \beta _{j}}$

Yine, daha geleneksel denklemler şunlardır:

${\displaystyle \log {\frac {p}{1-p}}=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots + \beta _{m}x_{m}}$

ve

${\displaystyle p={\frac {1}{1+b^{-(\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots) +\beta _{m}x_{m})}}}}$

genellikle nerede . ${\görüntüleme stili b=e}$

Model uydurma

Lojistik regresyon önemli bir makine öğrenme algoritmasıdır. Amaç, deneysel veri verilen rastgele bir değişkenin 0 veya 1 olma olasılığını modellemektir . ${\görüntüleme stili Y}$

ile parametrelenen genelleştirilmiş bir doğrusal model işlevi düşünün , ${\görüntüleme stili\teta }$

${\displaystyle h_{\theta }(X)={\frac {1}{1+e^{-\theta ^{T}X}}}=\Pr(Y=1\mid X;\theta )}$

Öyleyse,

${\displaystyle \Pr(Y=0\mid X;\theta )=1-h_{\theta }(X)}$

ve , tarafından verildiğini gördüğümüz için , şimdi örnekteki tüm gözlemlerin bağımsız olarak Bernoulli dağılımı olduğunu varsayarak olabilirlik fonksiyonunu hesaplıyoruz , ${\displaystyle Y\in \{0,1\}}$${\displaystyle \Pr(y\mid X;\theta )}$${\displaystyle \Pr(y\mid X;\theta )=h_{\theta }(X)^{y}(1-h_{\theta }(X))^{(1-y)}.}$

${\displaystyle {\begin{hizalanmış}L(\theta \mid y;x)&=\Pr(Y\mid X;\theta )\\&=\prod _{i}\Pr(y_{i}\ mid x_{i};\theta )\\&=\prod _{i}h_{\theta }(x_{i})^{y_{i}}(1-h_{\theta }(x_{i} ))^{(1-y_{i})}\end{hizalı}}}$

Tipik olarak, günlük olasılığı maksimize edilir,

${\displaystyle N^{-1}\log L(\theta \mid y;x)=N^{-1}\sum _{i=1}^{N}\log \Pr(y_{i}\ orta x_{i};\theta )}$

gradyan inişi gibi optimizasyon teknikleri kullanılarak maksimize edilir .

Çiftlerin temel dağılımdan düzgün bir şekilde çizildiğini varsayarsak , o zaman büyük N limitinde  , ${\görüntüleme stili (x,y)}$

${\displaystyle {\begin{hizalanmış}&\lim \limits _{N\rightarrow +\infty}N^{-1}\sum _{i=1}^{N}\log \Pr(y_{i} \mid x_{i};\theta )=\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\Pr(X=x,Y= y)\log \Pr(Y=y\mid X=x;\theta )\\[6pt]={}&\sum _{x\in {\mathcal {X}}}\sum _{y\in {\matematik {Y}}}\Pr(X=x,Y=y)\sol(-\log {\frac {\Pr(Y=y\orta X=x)}{\Pr(Y=y\) mid X=x;\theta )}}+\log \Pr(Y=y\mid X=x)\sağ)\\[6pt]={}&-D_{\text{KL}}(Y\paralel Y_{\theta})-H(Y\mid X)\end{hizalı}}}$

nerede olduğunu koşullu entropi ve bir Kullback-Leibler sapma . Bu, bir modelin log olasılığını en üst düzeye çıkararak, modelinizin KL sapmasını en yüksek entropi dağılımından en aza indirdiğiniz sezgisine yol açar. Parametrelerinde en az varsayımı yapan modeli sezgisel olarak aramak. ${\görüntüleme stili H(Y\orta X)}$${\displaystyle D_{\metin{KL}}}$

"On kuralı"

Yaygın olarak kullanılan bir genel kural olan " onda bir kural ", lojistik regresyon modellerinin, açıklayıcı değişken (EPV) başına minimum yaklaşık 10 olaya dayalı olması durumunda açıklayıcı değişkenler için kararlı değerler verdiğini belirtir; burada olay , bağımlı değişkende daha az sıklıkta olan kategoriye ait durumları gösterir. Bu nedenle, araştırmaya katılanların bir kısmında gerçekleşmesi beklenen bir olay (örn. miyokard enfarktüsü ) için açıklayıcı değişkenleri kullanmak üzere tasarlanmış bir çalışma , toplam katılımcı gerektirecektir . Ancak, simülasyon çalışmalarına dayanan ve güvenli bir teorik temelden yoksun olan bu kuralın güvenilirliği konusunda önemli tartışmalar vardır. Bazı yazarlara göre kural, bazı durumlarda aşırı muhafazakardır, yazarlar, "Eğer (biraz öznel olarak) güven aralığı kapsamını yüzde 93'ten az, tip I hatayı yüzde 7'den büyük veya yüzde 15'ten büyük göreli önyargı olarak kabul edersek, Sorunlu, sonuçlarımız 2-4 EPV ile problemlerin oldukça sık olduğunu, 5-9 EPV ile nadir olduğunu ve 10-16 EPV ile hala gözlemlendiğini göstermektedir.Her problemin en kötü örnekleri 5-9 EPV ile şiddetli değildi ve genellikle karşılaştırılabilir 10-16 EPV olanlar". ${\görüntüleme stili k}$${\görüntüleme stili p}$${\görüntüleme stili 10k/p}$

Diğerleri, farklı kriterler kullanarak yukarıdakilerle tutarlı olmayan sonuçlar bulmuştur. Yararlı bir kriter, uygun modelin, model geliştirme örneğinde elde ettiği göründüğü gibi, yeni bir örnekte de aynı tahmine dayalı ayrımcılığı elde etmesinin beklenip beklenmeyeceğidir. Bu kriter için aday değişken başına 20 olay gerekebilir. Ayrıca, 96 gözlemin, yalnızca modelin kesişimini, tahmin edilen olasılıklardaki hata payının 0.95 güven seviyesi ile ±0.1 olduğu kadar kesin olarak tahmin etmek için gerekli olduğu iddia edilebilir.

Maksimum olabilirlik tahmini (MLE)

Regresyon katsayıları genellikle maksimum olabilirlik tahmini kullanılarak tahmin edilir . Normal dağılmış artıklarla doğrusal regresyondan farklı olarak, olabilirlik fonksiyonunu maksimize eden katsayı değerleri için kapalı biçimli bir ifade bulmak mümkün değildir, bu nedenle bunun yerine yinelemeli bir süreç kullanılmalıdır; örneğin Newton'un yöntemi . Bu süreç, geçici bir çözümle başlar, geliştirilip geliştirilemeyeceğini görmek için biraz revize eder ve daha fazla iyileştirme yapılmayana kadar bu revizyonu tekrarlar, bu noktada sürecin yakınsadığı söylenir.

Bazı durumlarda model yakınsamaya ulaşamayabilir. Bir modelin yakınsama olmaması, yinelemeli süreç uygun çözümler bulamadığı için katsayıların anlamlı olmadığını gösterir. Yakınsama başarısızlığı birkaç nedenden dolayı meydana gelebilir: tahmin edicilerin vakalara oranının yüksek olması, çoklu bağlantı , seyreklik veya tam ayrılma .

• Değişkenlerin vakalara oranının yüksek olması, aşırı muhafazakar bir Wald istatistiği (aşağıda tartışılmıştır) ile sonuçlanır ve yakınsama olmamasına yol açabilir. Düzenli lojistik regresyon, özellikle bu durumda kullanılmak üzere tasarlanmıştır.
• Çoklu bağlantı, tahmin ediciler arasında kabul edilemez derecede yüksek korelasyonları ifade eder. Çoklu doğrusallık arttıkça katsayılar yansız kalır, ancak standart hatalar artar ve model yakınsama olasılığı azalır. Öngörücüler arasındaki çoklu doğrusallığı tespit etmek için, çoklu doğrusallığın kabul edilemez derecede yüksek olup olmadığını değerlendirmek için kullanılan tolerans istatistiğini incelemek amacıyla, ilgilenilen kestiricilerle doğrusal bir regresyon analizi yapılabilir.
• Verilerdeki seyreklik, büyük oranda boş hücreye (sıfır sayımlı hücreler) sahip olmak anlamına gelir. Sıfır hücre sayısı, özellikle kategorik öngörücülerle sorunludur. Sürekli öngörücülerle model, sıfır hücre sayıları için değerler çıkarabilir, ancak kategorik öngörücülerde durum böyle değildir. Sıfırın doğal logaritması tanımsız bir değer olduğundan, modelin nihai çözümüne ulaşılamadığından model, kategorik tahminciler için sıfır hücre sayılarıyla yakınsamayacaktır. Bu sorunu çözmek için araştırmacılar kategorileri teorik olarak anlamlı bir şekilde daraltabilir veya tüm hücrelere bir sabit ekleyebilir.
• Yakınsama eksikliğine yol açabilecek diğer bir sayısal sorun, tahmin edicilerin kriteri mükemmel bir şekilde öngördüğü duruma atıfta bulunan tam ayırmadır - tüm durumlar doğru bir şekilde sınıflandırılır. Bu gibi durumlarda, bir tür hata olması muhtemel olduğundan, veriler yeniden incelenmelidir.
• Ayrıca, indeks fonksiyonu için parametrik bir formun varsayımlarından kaçınan ve link fonksiyonunun seçimine karşı dayanıklı olan yerel-olabilirlik veya parametrik olmayan yarı-olabilirlik yöntemleri gibi yarı-parametrik veya parametrik olmayan yaklaşımlar da alınabilir (örn. probit veya logit).

Çapraz entropi Kaybı işlevi

İkili sınıflandırma için lojistik regresyonun kullanıldığı makine öğrenimi uygulamalarında MLE, Çapraz entropi kaybı işlevini en aza indirir .

Yinelemeli olarak yeniden ağırlıklı en küçük kareler (IRLS)

İkili lojistik regresyon ( veya ), örneğin, Newton'un yöntemini kullanarak bir Bernoulli dağıtılmış sürecinin log olasılığını maksimize etmeye eşdeğer olan yinelemeli olarak yeniden ağırlıklı en küçük kareler (IRLS) kullanılarak hesaplanabilir . Problem, parametreler , açıklayıcı değişkenler ve Bernoulli dağılımının beklenen değeri ile vektör matrisi biçiminde yazılırsa , parametreler aşağıdaki yinelemeli algoritma kullanılarak bulunabilir: ${\görüntüleme stili y=0}$${\görüntüleme stili y=1}$${\displaystyle \mathbf {w} ^{T}=[\beta _{0},\beta _{1},\beta _{2},\ldots ]}$${\displaystyle \mathbf {x} (i)=[1,x_{1}(i),x_{2}(i),\ldots ]^{T}}$${\displaystyle \mu (i)={\frac {1}{1+e^{-\mathbf {w} ^{T}\mathbf {x} (i)}}}}$${\displaystyle \mathbf {w} }$

${\displaystyle \mathbf {w} _{k+1}=\left(\mathbf {X} ^{T}\mathbf {S} _{k}\mathbf {X} \sağ)^{-1}\ mathbf {X} ^{T}\left(\mathbf {S} _{k}\mathbf {X} \mathbf {w} _{k}+\mathbf {y} -\mathbf {\boldsymbol {\mu } } _{k}\sağ)}$

çapraz ağırlık matrisi nerede , beklenen değerlerin vektörü, ${\displaystyle \mathbf {S} =\operatör adı {diag} (\mu (i)(1-\mu (i)))}$${\displaystyle {\boldsymbol {\mu }}=[\mu (1),\mu (2),\ldots ]}$

${\displaystyle \mathbf {X} ={\begin{bmatrix}1&x_{1}(1)&x_{2}(1)&\ldots \\1&x_{1}(2)&x_{2}(2)&\ ldots \\\vdots &\vdots &\vdots \end{bmatrix}}}$

Regresör matrisi ve yanıt değişkenlerinin vektörü. Daha fazla ayrıntı literatürde bulunabilir. ${\displaystyle \mathbf {y} (i)=[y(1),y(2),\ldots ]^{T}}$

Uyum iyiliğinin değerlendirilmesi

Ki bu uyumun iyi lineer regresyon modellerinde, genellikle kullanılarak ölçülür R ² . Bunun lojistik regresyonda doğrudan bir analogu olmadığı için, bunun yerine aşağıdakileri içeren çeşitli yöntemler kullanılabilir.

Sapma ve olabilirlik oranı testleri

Doğrusal regresyon analizinde, varyansın kareler toplamı hesaplamaları yoluyla bölünmesiyle ilgilenilir - kriterdeki varyans, esas olarak, tahmin ediciler ve artık varyans tarafından açıklanan varyansa bölünür. Lojistik regresyon analizinde, kareler toplamı hesaplamaları yerine sapma kullanılır. Sapma, doğrusal regresyondaki kareler hesaplamalarının toplamına benzer ve bir lojistik regresyon modelindeki verilere uyum eksikliğinin bir ölçüsüdür. "Doymuş" bir model mevcut olduğunda (teorik olarak mükemmel bir model), verilen bir model ile doymuş model karşılaştırılarak sapma hesaplanır. Bu hesaplama, olasılık-oran testini verir :

${\displaystyle D=-2\ln {\frac {\text{uyumlu modelin olasılığı}}{\text{doymuş modelin olasılığı}}}.}$

Yukarıdaki denklemde D sapmayı, ln ise doğal logaritmayı temsil eder. Bu olabilirlik oranının logaritması (uyumlu modelin doymuş modele oranı) negatif bir değer üretecektir, dolayısıyla negatif bir işarete ihtiyaç duyulacaktır. D'nin yaklaşık bir ki-kare dağılımını takip ettiği gösterilebilir . Takılan model doymuş modelden daha az saptığı için daha küçük değerler daha iyi uyumu gösterir. Ki-kare dağılımı üzerinde değerlendirildiğinde, anlamlı olmayan ki-kare değerleri çok az açıklanamayan varyansı ve dolayısıyla iyi model uyumunu gösterir. Tersine, anlamlı bir ki-kare değeri, varyansın önemli bir miktarının açıklanmadığını gösterir.

Doymuş model mevcut olmadığında (genel bir durum), sapma basitçe −2·(uyumlu modelin log olasılığı) olarak hesaplanır ve doymuş modelin log olasılığına yapılan referans zarar vermeden takip eden her şeyden çıkarılabilir.

Lojistik regresyonda iki sapma ölçüsü özellikle önemlidir: sıfır sapma ve model sapma. Boş sapma, yalnızca kesişen ("öngörücü yok" anlamına gelen) bir model ile doymuş model arasındaki farkı temsil eder. Model sapması, en az bir tahmin ediciye sahip bir model ile doymuş model arasındaki farkı temsil eder. Bu bağlamda, boş model, tahmin edici modellerin karşılaştırılacağı bir temel sağlar. Sapmanın belirli bir model ile doymuş model arasındaki farkın bir ölçüsü olduğu göz önüne alındığında, daha küçük değerler daha iyi uyumu gösterir. Bu nedenle, bir tahmin edicinin veya tahmin ediciler kümesinin katkısını değerlendirmek için, sıfır sapmadan model sapması çıkarılabilir ve serbestlik dereceleri tahmin edilen parametre sayısındaki farka eşit olan bir ki-kare dağılımındaki fark değerlendirilebilir . ${\displaystyle \chi _{sp}^{2},}$

İzin vermek

${\displaystyle {\begin{aligned}D_{\text{null}}&=-2\ln {\frac {\text{null model olasılığı}}{\text{doymuş model olasılığı}}}\\ [6pt]D_{\text{takılmış}}&=-2\ln {\frac {\text{uyumlu model olasılığı}}{\text{doymuş model olasılığı}}}.\end{hizalı}}}$

O zaman ikisinin farkı şudur:

${\displaystyle {\begin{aligned}D_{\text{null}}-D_{\text{takılmış}}&=-2\left(\ln {\frac {\text{boş model olasılığı}}{\ metin{doymuş modelin olasılığı}}}-\ln {\frac {\text{uyumlu modelin olasılığı}}{\text{doymuş modelin olasılığı}}}\sağ)\\[6pt]&=-2 \ln {\frac {\left({\dfrac {\text{boş model olasılığı}}{\text{doymuş model olasılığı}}}\sağ)}{\left({\dfrac {\text{olasılık) uygun modelin}}{\text{doymuş modelin olasılığı}}}\sağ)}}\\[6pt]&=-2\ln {\frac {\text{boş modelin olasılığı}}{\text {uyumlu model olasılığı}}}.\end{hizalı}}}$

Model sapması sıfır sapmadan önemli ölçüde küçükse, tahmin edicinin veya tahmin ediciler kümesinin modelin uyumunu önemli ölçüde iyileştirdiği sonucuna varılabilir. Bu, tahminin önemini değerlendirmek için doğrusal regresyon analizinde kullanılan F- testine benzer .

Sözde-R-kare

Doğrusal regresyonda kareli çoklu korelasyon, R ², yordayıcılar tarafından açıklanan kriterdeki varyans oranını temsil ettiği için uyumun iyiliğini değerlendirmek için kullanılır. Lojistik regresyon analizinde, üzerinde mutabık kalınan benzer bir ölçü yoktur, ancak her birinin sınırlamaları olan birkaç rekabet eden ölçü vardır.

Bu sayfada en sık kullanılan dört endeks ve daha az kullanılan bir endeks incelenmektedir:

• Olasılık oranı R ² _L
• Cox ve Snell R ² _CS
• Nagelkerke R ² _N
• McFadden R ² _McF
• Tjur R ² _T

R ² _L Cohen tarafından verilir:

${\displaystyle R_{\text{L}}^{2}={\frac {D_{\text{null}}-D_{\text{fitted}}}}{D_{\text{null}}}}. }$

Bu, doğrusal regresyondaki kare çoklu korelasyonlara en benzer indekstir. Bu sapma varyasyon benzer bir ölçüsü olarak tedavi edilebilir ancak aynı değildir, burada sapma orantılı bir azalmayı temsil etmektedir varyans olarak doğrusal regresyon analizi. Olasılık oranı bir kısıtlaması R ² o kadar monoton olarak mutlaka olasılık oranı arttıkça artmaz ve zorunlu olarak oranı azalır oran olarak azalmaz, yani risk oranı ile ilgili değildir olmasıdır.

R ² _CS , lineer regresyondan R ² değeriyle ilgili alternatif bir uyum iyiliği indeksidir . Şunlar tarafından verilir:

${\displaystyle {\begin{aligned}R_{\text{CS}}^{2}&=1-\left({\frac {L_{0}}{L_{M}}}\sağ)^{2 /n}\\[5pt]&=1-e^{2(\ln(L_{0})-\ln(L_{M}))/n}\end{hizalı}}}$

burada L _M ve L ₀ , sırasıyla takılan model ve boş model için olasılıklardır. Cox ve Snell indeksi, maksimum değeri olduğu için sorunludur . Bu üst sınır en yüksek 0.75 olabilir, ancak vakaların marjinal oranı küçük olduğunda kolayca 0.48'e kadar düşebilir. ${\displaystyle 1-L_{0}^{2/n}}$

R ² _N , Cox ve Snell R ² için bir düzeltme sağlar, böylece maksimum değer 1'e eşit olur. Bununla birlikte, Cox ve Snell ve olabilirlik oranı R ²'ler birbirleriyle Nagelkerke R ² ile olduğundan daha fazla uyum gösterir . Cox ve Snell endeksi bu değerde sınırlandırıldığından, 0,75'i aşan değerler için bu durum geçerli olmayabilir elbette. Olasılık oranı R, o en çok benzeyen bir şekilde ² genellikle alternatifler tercih edilir R ² lineer regresyon baz oranından bağımsızdır (Cox ve Snell ve Nagelkerke iki R vakaların oranı olarak ²s artışı 0 ila 0.5 yükselecek) ve 0 ile 1 arasında değişir.

R ² _McF şu şekilde tanımlanır:

${\displaystyle R_{\text{McF}}^{2}=1-{\frac {\ln(L_{M})}{\ln(L_{0})}},}$

Allison tarafından R ² _CS yerine tercih edilmektedir. R ² _McF ve R ² _CS iki ifadesi sırasıyla şu şekilde ilişkilidir:

${\displaystyle {\begin{matrix}R_{\text{CS}}^{2}=1-\left({\dfrac {1}{L_{0}}}\sağ)^{\frac {2( R_{\text{McF}}^{2})}{n}}\\[1.5em]R_{\text{McF}}^{2}=-{\dfrac {n}{2}}\cdot {\dfrac {\ln(1-R_{\text{CS}}^{2})}{\ln L_{0}}}\end{matrix}}}$

Ancak Allison, şimdi Tjur tarafından geliştirilen nispeten yeni bir ölçü olan R ² _T'yi tercih ediyor . İki adımda hesaplanabilir:

1. Bağımlı değişkenin her düzeyi için, bir olayın tahmin edilen olasılıklarının ortalamasını bulun.
2. Bu araçlar arasındaki farkın mutlak değerini alın

Sözde R ² istatistiklerini yorumlarken dikkatli olunması gerekir . Uyum bu endeksler olarak adlandırılır nedeni sahte R ² onlar hata oransal azalma temsil kalmamasıdır R ²da doğrusal regresyon yapar. Doğrusal regresyon , hata varyansının kriterin tüm değerleri için aynı olduğunu, homoskedastisiteyi varsayar . Lojistik regresyon her zaman değişen varyanslı olacaktır - tahmin edilen puanın her değeri için hata varyansları farklıdır. Tahmin edilen puanın her değeri için, hatadaki orantılı azalmanın farklı bir değeri olacaktır. Nedenle, düşünmek uygunsuz R lojistik regresyon içinde evrensel anlamda yanlışlıkla orantılı azalma olarak ².

Hosmer-Lemeshow testi

Hosmer-Lemeshow testi asimptotik bir izleyen bir deney istatistik kullanır dağılımını gözlenen olay oranları modeli nüfusun alt gruplarda beklenen etkinlik oranlarını maç olsun veya olmasın değerlendirmek. Bu test, bazı istatistikçiler tarafından, tahmin edilen olasılıkların keyfi olarak gruplandırılmasına ve göreceli olarak düşük güce bağlı olması nedeniyle modası geçmiş olarak kabul edilir. ${\displaystyle \chi ^{2}}$

katsayılar

Modeli yerleştirdikten sonra, araştırmacıların bireysel tahmin edicilerin katkısını incelemek isteyecekleri muhtemeldir. Bunu yapmak için regresyon katsayılarını incelemek isteyeceklerdir. Doğrusal regresyonda, regresyon katsayıları, tahmin edicideki her birim değişiklik için kriterdeki değişikliği temsil eder. Ancak lojistik regresyonda, regresyon katsayıları, tahmin edicideki her birim değişiklik için logitteki değişikliği temsil eder. Logitin sezgisel olmadığı göz önüne alındığında, araştırmacılar muhtemelen bir tahmin edicinin regresyon katsayısının üstel işlevi üzerindeki etkisine – olasılık oranı (bkz. tanıma bakın ). Doğrusal regresyonda, bir regresyon katsayısının önemi, bir t testi hesaplanarak değerlendirilir . Lojistik regresyonda, bireysel bir tahmin edicinin önemini değerlendirmek için tasarlanmış birkaç farklı test vardır, özellikle olabilirlik oranı testi ve Wald istatistiği.

Olasılık oranı testi

Olabilirlik-oran testi model uyumunu değerlendirmek için, yukarıda tartışılan aynı zamanda, belirli bir model için ayrı ayrı "belirleyicileri" katkısını araştırmak için tavsiye edilen bir işlemdir. Tek bir öngörücü model durumunda, tek bir serbestlik derecesine sahip ki-kare dağılımında kestirici modelin sapması ile boş modelin sapması basitçe karşılaştırılır. Öngörü modeli önemli ölçüde daha küçük sapmaya sahipse (iki modelin serbestlik derecelerindeki farkı kullanarak ki-kare ile karşılaştırın), o zaman "öngörücü" ile sonuç arasında önemli bir ilişki olduğu sonucuna varılabilir. Bazı yaygın istatistiksel paketler (örneğin SPSS) olabilirlik oranı test istatistiklerini sağlamasına rağmen, bu yoğun hesaplamalı test olmadan çoklu lojistik regresyon durumunda bireysel tahmin edicilerin katkısını değerlendirmek daha zor olacaktır. Bireysel tahmin edicilerin katkısını değerlendirmek için, her bir tahmin edicinin katkısını belirlemek için her yeni modeli bir öncekiyle karşılaştırarak tahmin edicilere hiyerarşik olarak girilebilir. İstatistikçiler arasında sözde "adım adım" prosedürlerin uygunluğu hakkında bazı tartışmalar var. Korku, nominal istatistiksel özellikleri koruyamama ve yanıltıcı hale gelmeleridir.

Wald istatistiği

Alternatif olarak, belirli bir modelde bireysel tahmin edicilerin katkısını değerlendirirken, Wald istatistiğinin önemi incelenebilir . Doğrusal regresyondaki t- testine benzer Wald istatistiği, katsayıların önemini değerlendirmek için kullanılır. Wald istatistiği, regresyon katsayısının karesinin, katsayının standart hatasının karesine oranıdır ve ki-kare dağılımı olarak asimptotik olarak dağıtılır.

${\displaystyle W_{j}={\frac {\beta _{j}^{2}}{SE_{\beta _{j}}^{2}}}}$

Birkaç istatistiksel paket (örneğin, SPSS, SAS) bireysel öngörücülerin katkısını değerlendirmek için Wald istatistiğini rapor etse de, Wald istatistiğinin sınırlamaları vardır. Regresyon katsayısı büyük olduğunda, regresyon katsayısının standart hatası da II . Tip hata olasılığını artırarak daha büyük olma eğilimindedir . Wald istatistiği, veriler seyrek olduğunda da önyargılı olma eğilimindedir.

Vaka kontrol örneklemesi

Diyelim ki vakalar nadir. O zaman onları popülasyondaki yaygınlıklarından daha sık örneklemek isteyebiliriz. Örneğin 10.000'de 1 kişiyi etkileyen bir hastalık olduğunu varsayalım ve verilerimizi toplamak için tam bir fizik muayene yapmamız gerekiyor. Sadece birkaç hastalıklı birey için veri elde etmek için binlerce sağlıklı insanın fiziksel muayenesini yapmak çok pahalı olabilir. Böylece daha fazla hastalıklı bireyi, belki de tüm nadir sonuçları değerlendirebiliriz. Bu aynı zamanda geriye dönük örneklemedir veya eşdeğer olarak dengesiz veri olarak adlandırılır. Genel bir kural olarak, vaka sayısının beş katı oranında örnekleme kontrolleri, yeterli kontrol verisi üretecektir.

Lojistik regresyon, rastgele örneklenmiş verilerden ziyade dengesiz veriler üzerinde tahmin edilebilmesi ve yine de her bir bağımsız değişkenin sonuç üzerindeki etkilerinin doğru katsayı tahminlerini vermesi bakımından benzersizdir. Yani bu tür verilerden lojistik bir model oluşturursak, model genel popülasyonda doğruysa , parametre dışındaki tüm parametreler doğrudur . Gerçek prevalansı biliyorsak aşağıdaki gibi düzeltebiliriz : ${\görüntüleme stili \beta _{j}}$${\görüntüleme stili \beta _{0}}$${\görüntüleme stili \beta _{0}}$

${\displaystyle {\widehat {\beta }}_{0}^{*}={\widehat {\beta }}_{0}+\log {\frac {\pi }}- \log {{\tilde {\pi }} \over {1-{\tilde {\pi }}}}}$

gerçek prevalans nerede ve örnekteki prevalans. ${\görüntüleme stili\pi }$${\ Displaystyle {\tilde {\pi }}}$

Resmi matematiksel belirtim

Daha genel modellerin farklı türlerine uyan çeşitli eşdeğer lojistik regresyon özellikleri vardır. Bu farklı özellikler, farklı türde faydalı genellemelere izin verir.

Kurmak

Lojistik regresyonun temel kurulumu aşağıdaki gibidir. Bize N nokta içeren bir veri seti verildi . Her i noktası , bir dizi m girdi değişkeni x _{1, i} ... x _m,i ( bağımsız değişkenler , tahmin değişkenleri, özellikler veya nitelikler olarak da adlandırılır ) ve bir ikili sonuç değişkeni Y _i'den ( bağımlı olarak da bilinir) oluşur. değişken , yanıt değişkeni, çıktı değişkeni veya sınıf), yani yalnızca 0 (genellikle "hayır" veya "başarısızlık" anlamına gelir) veya 1 (genellikle "evet" veya "başarı" anlamına gelir) iki olası değerini alabilir. Lojistik regresyonun amacı, sonuç değişkeninin tahmine dayalı bir modelini oluşturmak için veri setini kullanmaktır.

Doğrusal regresyonda olduğu gibi, Y _i sonuç değişkenlerinin x _{1, i} ... x _m,i açıklayıcı değişkenlere bağlı olduğu varsayılır .

açıklayıcı değişkenler

Açıklayıcı değişkenler herhangi bir tipte olabilir : gerçek değerli , ikili , kategorik , vb. Ana ayrım, sürekli değişkenler ve ayrık değişkenler arasındadır .

(İkiden fazla olası seçeneğe atıfta bulunan ayrık değişkenler tipik olarak kukla değişkenler (veya gösterge değişkenleri ) kullanılarak kodlanır , yani ayrık değişkenin her olası değeri için 0 veya 1 değerini alan ayrı açıklayıcı değişkenler oluşturulur ve 1 anlamı " değişken verilen değere sahip" ve 0, "değişken bu değere sahip değil" anlamına gelir.)

Dış değişkenler

Biçimsel olarak, sonuçlar , Y _ı olarak tarif edilmektedir Bernoulli dağıtılmış her bir sonuç gözlemlenmeyen olasılığı ile belirlenir veriler, p _ı eldeki sonucu özeldir, fakat açıklayıcı değişkenler ile ilgili. Bu, aşağıdaki eşdeğer formlardan herhangi birinde ifade edilebilir:

${\displaystyle {\begin{aligned}Y_{i}\mid x_{1,i},\ldots ,x_{m,i}\ &\sim \operatöradı {Bernoulli} (p_{i})\\\operatöradı {\mathcal {E}} [Y_{i}\mid x_{1,i},\ldots ,x_{m,i}]&=p_{i}\\\Pr(Y_{i}=y\mid x_{1,i},\ldots ,x_{m,i})&={\begin{cases}p_{i}&{\text{if }}y=1\\1-p_{i}&{ \text{if }}y=0\end{durumlar}}\\\Pr(Y_{i}=y\mid x_{1,i},\ldots ,x_{m,i})&=p_{i }^{y}(1-p_{i})^{(1-y)}\end{hizalı}}}$

Bu dört satırın anlamları:

1. İlk hat ifade olasılık dağılımını her Y _i : açıklayıcı değişkenler koşuluna bağlı olarak bir, aşağıdaki Bernoulli dağılımı parametreleri ile p _i , 1 sonuçları olasılığı deneme için i . Yukarıda belirtildiği gibi, her denemenin kendi açıklayıcı değişkenleri olduğu gibi, her bir ayrı denemenin kendi başarı olasılığı vardır. Başarı olasılığı p _i gözlenmez, bu olasılık kullanarak tek bir Bernoulli deneme sadece sonuçları.
2. İkinci satır aslında ifade beklenen değer , her bir Y _i başarı olasılığı eşittir p _i Bernoulli dağılımı hakkında genel bir özelliğidir. Biz başarı aynı olasılık kullanarak Bernoulli denemelerinin çok sayıda çalıştırırsanız Başka bir deyişle, p _i , o zaman tüm 1 ve 0 sonuçların ortalama almak, sonuç yakın olacaktır p _i . Bunun nedeni, bu şekilde bir ortalama yapmanın, temel başarı olasılığına yakınsamasını beklediğimiz, görülen başarıların oranını hesaplamasıdır.
3. Üçüncü satır , iki olası sonucun her birini görme olasılığını belirterek, Bernoulli dağılımının olasılık kütle fonksiyonunu yazar .
4. Dördüncü satır, ayrı durumlar yazmaktan kaçınan ve belirli hesaplama türleri için daha uygun olan olasılık kütle fonksiyonunu yazmanın başka bir yoludur. Bu, Y _i'nin sadece 0 veya 1 değerini alabileceği gerçeğine dayanır. Her durumda, üslerden biri, altındaki değeri "seçerek", diğeri 0 ise, altındaki değeri "iptal ederek" 1 olacaktır. o. Dolayısıyla, sonuç, ya bir p _i - veya 1  p _ı önceki çizgi gibi.

Doğrusal tahmin işlevi

Lojistik regresyon temel fikri daha önce için geliştirilmiş bir mekanizma kullanmaktır lineer regresyon olasılığı modelleyerek p _ı bir kullanılarak doğrusal tahmin fonksiyonu , diğer bir deyişle doğrusal bir kombinasyonu açıklayıcı değişkenlerin ve bir dizi regresyon katsayısı eldeki modeline özgü olduğu ama tüm denemeler için aynı. Belirli bir veri noktası i için doğrusal tahmin işlevi şu şekilde yazılır: ${\görüntüleme stili f(i)}$

${\displaystyle f(i)=\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{m}x_{m,i},}$

burada vardır regresyon katsayısı sonuç üzerinde belirli açıklayıcı değişkeninin etkisini göstermektedir. ${\displaystyle \beta _{0},\ldots ,\beta _{m}}$

Model genellikle aşağıdaki gibi daha kompakt bir forma getirilir:

• Regresyon katsayıları β ₀ , β ₁ , ..., β _m , m  + 1 boyutunda tek bir β vektörü olarak gruplanır .
• Her veri noktası i için, kesme katsayısı β _0'a karşılık gelen sabit 1 değeriyle ek bir açıklayıcı sözde değişken x _{0, i} eklenir .
• Elde edilen açıklayıcı değişkenler x _{0, i} , x _{1, i} , ..., x _m,i daha sonra m  + 1 boyutunda tek bir X _i vektörü halinde gruplandırılır .

Bu, doğrusal tahmin fonksiyonunu aşağıdaki gibi yazmayı mümkün kılar:

${\displaystyle f(i)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i},}$

iki vektör arasındaki bir nokta çarpımı için gösterimi kullanarak .

Genelleştirilmiş bir doğrusal model olarak

Lojistik regresyon tarafından kullanılan ve onu standart lineer regresyondan ve ikili değerli sonuçlar için kullanılan diğer regresyon analizi türlerinden ayıran belirli model, belirli bir sonucun olasılığının lineer tahmin fonksiyonuna bağlanma şeklidir:

${\displaystyle \operatöradı {logit} (\operatöradı {\mathcal {E}} [Y_{i}\mid x_{1,i},\ldots ,x_{m,i}])=\operatöradı {logit} ( p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\sağ)=\beta _{0}+\beta _{1}x_{1, i}+\cdots +\beta _{m}x_{m,i}}$

Yukarıda açıklanan daha kompakt gösterim kullanılarak yazılmıştır, bu:

${\displaystyle \operatöradı {logit} (\operatöradı {\mathcal {E}} [Y_{i}\mid \mathbf {X} _{i}])=\operatöradı {logit} (p_{i})=\ ln \left({\frac {p_{i}}{1-p_{i}}}\sağ)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}$

Bu formülasyon, bir tür genelleştirilmiş doğrusal model olarak lojistik regresyonu ifade eder ; bu , değişkenin beklenen değerinin bir tür keyfi dönüşümüne yukarıdaki formun doğrusal bir tahmin fonksiyonunu uydurarak çeşitli olasılık dağılımlarına sahip değişkenleri tahmin eder.

Logit fonksiyonunu (oranların doğal logu) kullanarak dönüştürme sezgisi yukarıda açıklanmıştır. Ayrıca, olasılığı (0 ile 1 arasında sınırlanmış) bir değişkene dönüştürmenin pratik etkisine sahiptir - böylece denklemin sağ tarafındaki doğrusal tahmin fonksiyonunun potansiyel aralığını eşleştirir. ${\displaystyle (-\infty ,+\infty )}$

Olasılıkları de o Not p _I ve regresyon katsayısı gözlenmemiş olan ve bunları belirleyen araçlar modelinin kendisinde bir parçası değildir. Bunlar tipik olarak , gözlemlenen verilere en iyi uyan değerleri bulan (yani halihazırda gözlemlenen veriler için en doğru tahminleri veren) bir tür optimizasyon prosedürü, örneğin maksimum olabilirlik tahmini tarafından belirlenir , genellikle olası olmayanları hariç tutmaya çalışan düzenlileştirme koşullarına tabidir. değerler, örneğin herhangi bir regresyon katsayısı için aşırı büyük değerler. Bir düzenleme koşulunun kullanılması , maksimum olasılığın bir uzantısı olan maksimum a posteriori (MAP) tahmini yapmaya eşdeğerdir . (Düzenleme en yaygın olarak, katsayılar üzerine sıfır ortalamalı bir Gauss ön dağılımı yerleştirmeye eşdeğer olan bir kare düzenlileştirme işlevi kullanılarak yapılır , ancak diğer düzenleyiciler de mümkündür.) Düzenlileştirmenin kullanılıp kullanılmadığını bulmak genellikle mümkün değildir. kapalı biçimli bir çözüm; bunun yerine, yinelemeli olarak yeniden ağırlıklı en küçük kareler (IRLS) gibi yinelemeli bir sayısal yöntem veya günümüzde daha yaygın olarak L-BFGS yöntemi gibi bir Newton benzeri yöntem kullanılmalıdır .

β _j parametre tahminlerinin yorumlanması , açıklayıcı değişken j'deki bir birim değişikliğin oranların logaritması üzerindeki toplam etkisi gibidir . Örneğin, ikili bir açıklayıcı değişken söz konusu olduğunda, cinsiyet , örneğin kadınlara kıyasla erkeklerin sonuca sahip olma ihtimalinin tahminidir. ${\görüntüleme stili e^{\beta }}$

Eşdeğer bir formül, lojistik işlevi olan logit işlevinin tersini kullanır , yani:

${\displaystyle \operatöradı {\mathcal {E}} [Y_{i}\mid \mathbf {X} _{i}]=p_{i}=\operatöradı {logit} ^{-1}({\boldsymbol { \beta }}\cdot \mathbf {X} _{i})={\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}} }}}$

Formül ayrıca bir olasılık dağılımı olarak da yazılabilir (özellikle, bir olasılık kütle fonksiyonu kullanılarak ):

${\displaystyle \Pr(Y_{i}=y\mid \mathbf {X} _{i})={p_{i}}^{y}(1-p_{i})^{1-y}= \left({\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf { X} _{i}}}}\sağ)^{y}\left(1-{\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}{ 1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\sağ)^{1-y}={\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}\cdot y}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}}$

Gizli değişken modeli olarak

Yukarıdaki model, bir gizli değişken modeli olarak eşdeğer bir formülasyona sahiptir . Bu formülasyon, ayrık seçim modelleri teorisinde yaygındır ve çoklu, ilişkili seçimlerle belirli daha karmaşık modellere genişletmeyi ve lojistik regresyonu yakından ilişkili probit modeliyle karşılaştırmayı kolaylaştırır .

Her i denemesi için , aşağıdaki gibi dağıtılan sürekli bir gizli değişken Y _i ^* (yani gözlemlenmemiş bir rastgele değişken ) olduğunu hayal edin :

${\displaystyle Y_{i}^{\ast }={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon \,}$

nerede

${\displaystyle \varepsilon \sim \operatöradı {Lojistik} (0,1)\,}$

yani gizli değişken, doğrudan doğrusal tahmin fonksiyonu ve standart bir lojistik dağılıma göre dağıtılan bir toplamalı rastgele hata değişkeni cinsinden yazılabilir .

O zaman Y _i , bu gizli değişkenin pozitif olup olmadığının bir göstergesi olarak görülebilir:

${\displaystyle Y_{i}={\begin{cases}1&{\text{if }}Y_{i}^{\ast }>0\ {\text{ yani }}-\varepsilon <{\boldsymbol {\ beta }}\cdot \mathbf {X} _{i},\\0&{\text{aksi halde.}}\end{durumlar}}}$

Konum ve ölçeğin keyfi değerlere ayarlandığı genel bir lojistik dağılım yerine, hata değişkenini özel olarak standart bir lojistik dağılımla modelleme seçimi kısıtlayıcı görünüyor, ancak aslında öyle değil. Regresyon katsayılarını kendimiz seçebileceğimiz ve bunları sıklıkla hata değişkeninin dağılımının parametrelerindeki değişiklikleri dengelemek için kullanabileceğimiz akılda tutulmalıdır. Örneğin, sıfır olmayan bir konum parametresi ile bir lojistik hatasız değişken dağıtım ^ ı (ortalama ayarlar) sıfır konum parametresi, bir dağıtım eşdeğerdir μ kesişme katsayısına eklendi. Her iki durum da açıklayıcı değişkenlerin ayarlarından bağımsız olarak Y _i ^* için aynı değeri üretir . Benzer şekilde, rastgele bir ölçek parametresi s , ölçek parametresini 1'e ayarlamak ve ardından tüm regresyon katsayılarını s'ye bölmekle eşdeğerdir . İkinci durumda, elde edilen Y _i ^* değeri, tüm açıklayıcı değişken kümeleri için önceki duruma göre s faktörü kadar küçük olacaktır - ancak kritik olarak, her zaman 0'ın aynı tarafında kalacaktır ve dolayısıyla önde olacaktır. aynı Y _i seçimine.

(Bunun, ölçek parametresinin ilgisizliğinin, ikiden fazla seçeneğin mevcut olduğu daha karmaşık modellere taşınmayabileceğini tahmin ettiğini unutmayın.)

Bu formülasyonun, genelleştirilmiş doğrusal model açısından ve herhangi bir gizli değişken olmaksızın ifade edilen öncekine tam olarak eşdeğer olduğu ortaya çıktı . Bu aslında kullanılarak, aşağıdaki gibi gösterilebilir kümülatif dağılım fonksiyonu standart (CDF) lojistik dağıtım olan lojistik fonksiyon tersidir, logit fonksiyonu , yani

${\displaystyle \Pr(\varepsilon <x)=\operatöradı {logit} ^{-1}(x)}$

Sonra:

${\displaystyle {\begin{hizalanmış}\Pr(Y_{i}=1\mid \mathbf {X} _{i})&=\Pr(Y_{i}^{\ast }>0\mid \mathbf {X} _{i})\\[5pt]&=\Pr({\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon >0)\\[5pt]&= \Pr(\varepsilon >-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})\\[5pt]&=\Pr(\varepsilon <{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&&{\text{(lojistik dağılım simetrik olduğundan)}}\\[5pt]&=\operatöradı {logit} ^{-1}({\boldsymbol {\beta } }\cdot \mathbf {X} _{i})&\\[5pt]&=p_{i}&&{\text{(yukarıya bakın)}}\end{hizalı}}}$

Ayrık seçim modellerinde standart olan bu formülasyon, lojistik regresyon ("logit model") ile standart bir lojistik dağılım yerine standart bir normal dağılıma göre dağıtılan bir hata değişkeni kullanan probit modeli arasındaki ilişkiyi netleştirir . Hem lojistik hem de normal dağılımlar, temel tek modlu, "çan eğrisi" şekliyle simetriktir. Tek fark, lojistik dağılımın biraz daha ağır kuyruklara sahip olmasıdır , bu da uzak verilere daha az duyarlı olduğu anlamına gelir (ve dolayısıyla yanlış spesifikasyonları veya hatalı verileri modellemek için biraz daha sağlamdır ).

İki yönlü gizli değişken modeli

Yine başka bir formülasyon iki ayrı gizli değişken kullanır:

${\displaystyle {\begin{hizalanmış}Y_{i}^{0\ast }&={\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}+\varepsilon _{0 }\,\\Y_{i}^{1\ast }&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}+\varepsilon _{1}\,\ bitiş{hizalı}}}$

nerede

${\displaystyle {\begin{aligned}\varepsilon _{0}&\sim \operatöradı {EV} _{1}(0,1)\\\varepsilon _{1}&\sim \operatöradı {EV} _{ 1}(0,1)\end{hizalanmış}}}$

burada EV ₁ (0,1) standart bir tip-1 uç değer dağılımıdır : yani

${\displaystyle \Pr(\varepsilon _{0}=x)=\Pr(\varepsilon _{1}=x)=e^{-x}e^{-e^{-x}}}$

Sonra

${\displaystyle Y_{i}={\begin{vakalar}1&{\text{if }}Y_{i}^{1\ast }>Y_{i}^{0\ast },\\0&{\text {aksi halde.}}\end{durumlar}}}$

Bu model, bağımlı değişkenin her olası sonucu için ayrı bir gizli değişkene ve ayrı bir regresyon katsayıları grubuna sahiptir. Bu ayrımın nedeni, lojistik regresyonun çok terimli logit modelinde olduğu gibi çok sonuçlu kategorik değişkenlere genişletilmesini kolaylaştırmasıdır . Böyle bir modelde, her olası sonucu farklı bir regresyon katsayıları seti kullanarak modellemek doğaldır. Ayrı gizli değişkenlerin her birini, ilişkili seçimi yapmakla ilişkili teorik fayda olarak motive etmek ve böylece fayda teorisi açısından lojistik regresyonu motive etmek de mümkündür . (Fayda teorisi açısından, rasyonel bir aktör her zaman en büyük ilişkili faydaya sahip seçimi seçer.) Ekonomistler tarafından ayrık seçim modelleri formüle edilirken alınan yaklaşım budur , çünkü hem teorik olarak güçlü bir temel sağlar hem de modelle ilgili sezgileri kolaylaştırır. sırayla, çeşitli uzantı türlerini düşünmeyi kolaylaştırır. (Aşağıdaki örneğe bakın.)

Tip-1 uç değer dağılımının seçimi oldukça keyfi görünüyor, ancak matematiğin çalışmasını sağlıyor ve kullanımını rasyonel seçim teorisi yoluyla haklı çıkarmak mümkün olabilir .

Bu modelin önceki modele eşdeğer olduğu ortaya çıktı, ancak bu açık değil gibi görünüyor, çünkü artık iki set regresyon katsayısı ve hata değişkeni var ve hata değişkenleri farklı bir dağılıma sahip. Aslında, bu model aşağıdaki ikamelerle doğrudan bir öncekine indirgenir:

${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0}}$

${\displaystyle \varepsilon =\varepsilon _{1}-\varepsilon _{0}}$

Bunun için bir sezgi, en fazla iki değere dayalı olarak seçim yaptığımız için, kesin değerlerin değil, yalnızca farklarının önemli olduğu gerçeğinden gelir - ve bu , bir serbestlik derecesini etkin bir şekilde ortadan kaldırır . Bir diğer kritik gerçek ise, iki tip-1 uç değer dağılımlı değişkenin farkının lojistik bir dağılım olmasıdır, yani eşdeğerini şu şekilde gösterebiliriz: ${\displaystyle \varepsilon =\varepsilon _{1}-\varepsilon _{0}\sim \operatöradı {Lojistik} (0,1).}$

${\displaystyle {\begin{hizalanmış}\Pr(Y_{i}=1\mid \mathbf {X} _{i})={}&\Pr \left(Y_{i}^{1\ast }> Y_{i}^{0\ast }\mid \mathbf {X} _{i}\sağ)&\\[5pt]={}&\Pr \sol(Y_{i}^{1\ast }- Y_{i}^{0\ast }>0\mid \mathbf {X} _{i}\sağ)&\\[5pt]={}&\Pr \left({\boldsymbol {\beta }}_ {1}\cdot \mathbf {X} _{i}+\varepsilon _{1}-\left({\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}+\ varepsilon _{0}\right)>0\right)&\\[5pt]={}&\Pr \left(({\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{) i}-{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i})+(\varepsilon _{1}-\varepsilon _{0})>0\sağ)&\ \[5pt]={}&\Pr(({\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0})\cdot \mathbf {X} _{i}+ (\varepsilon _{1}-\varepsilon _{0})>0)&\\[5pt]={}&\Pr(({\boldsymbol {\beta }}_{1}-{\boldsymbol {\ beta }}_{0})\cdot \mathbf {X} _{i}+\varepsilon >0)&&{\text{(yedek }}\varepsilon {\text{ yukarıdaki gibi)}}\\[5pt] ={}&\Pr({\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon >0)&&{\text{(yedek }}{\boldsymbol {\beta }}{ \text{ yukarıdaki gibi)}}\\[5pt]={ }&\Pr(\varepsilon >-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&&{\text{(şimdi, yukarıdaki modelle aynı)}}\\[5pt]= {}&\Pr(\varepsilon <{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&\\[5pt]={}&\operatöradı {logit} ^{-1}( {\boldsymbol {\beta }}\cdot \mathbf {X} _{i})\\[5pt]={}&p_{i}\end{hizalı}}}$

Örnek

Örnek olarak, seçimin merkezin sağındaki bir parti, merkezin solundaki bir parti ve ayrılıkçı bir parti (örneğin Quebec'in Kanada'dan ayrılmasını isteyen Parti Québécois) arasında olduğu il düzeyinde bir seçimi düşünün . Daha sonra, her seçim için bir tane olmak üzere üç gizli değişken kullanırdık. Daha sonra, fayda teorisine uygun olarak , gizli değişkenleri , seçimlerin her birinin yapılmasından kaynaklanan faydayı ifade eden şekilde yorumlayabiliriz . Ayrıca regresyon katsayılarını, ilgili faktörün (yani açıklayıcı değişkenin) faydaya katkıda bulunma gücünü gösterdiği şeklinde de yorumlayabiliriz - veya daha doğrusu, açıklayıcı bir değişkendeki bir birim değişikliğinin belirli bir seçimin faydasını değiştirme miktarı. Bir seçmen, merkez sağ partisinin özellikle zengin insanlar üzerindeki vergileri düşürmesini bekleyebilir. Bu, düşük gelirli insanlara hiçbir fayda sağlamayacaktır, yani faydada bir değişiklik olmayacaktır (çünkü genellikle vergi ödemezler); orta gelirli insanlar için orta düzeyde faydaya (yani biraz daha fazla paraya veya orta düzeyde fayda artışına) neden olur; yüksek gelirli insanlar için önemli faydalar sağlayacaktır. Öte yandan, ortanın solundaki partinin vergileri artırması ve bunu alt ve orta sınıflar için artan refah ve diğer yardımlarla dengelemesi beklenebilir. Bu, düşük gelirli insanlar için önemli bir olumlu faydaya, orta gelirli insanlar için belki zayıf bir faydaya ve yüksek gelirli insanlar için önemli ölçüde olumsuz faydaya neden olacaktır. Son olarak, ayrılıkçı parti ekonomi üzerinde doğrudan bir eylemde bulunmayacak, sadece ayrılacaktı. Düşük gelirli veya orta gelirli bir seçmen, temelde bundan net bir fayda kazancı veya kaybı beklemeyebilir, ancak yüksek gelirli bir seçmen, şirket sahibi olması muhtemel olduğundan negatif fayda bekleyebilir ve bu da iş yapmakta daha zor olacaktır. böyle bir ortam ve muhtemelen para kaybedersiniz.

Bu sezgiler şu şekilde ifade edilebilir:

Farklı sonuçlar (parti seçimleri) ve açıklayıcı değişkenlerin farklı değerleri için tahmini regresyon katsayısı gücü

	Merkez sağ	Merkez-sol	Ayrılıkçı
Yüksek gelir	güçlü +	güçlü -	güçlü -
orta gelirli	ılımlı +	zayıf +	Yok
düşük gelirli	Yok	güçlü +	Yok

Bu açıkça gösteriyor ki

1. Her seçim için ayrı regresyon katsayıları setinin bulunması gerekir. Fayda açısından ifade edildiğinde, bu çok kolay görülebilir. Farklı seçimlerin net fayda üzerinde farklı etkileri vardır; dahası, etkiler her bireyin özelliklerine bağlı olarak karmaşık şekillerde değişir, bu nedenle her bir özellik için ayrı katsayı setleri olması gerekir, sadece fazladan seçim başına bir karakteristiğe değil.
2. Gelir sürekli bir değişken olmasına rağmen, fayda üzerindeki etkisi tek bir değişken olarak ele alınamayacak kadar karmaşıktır. Ya doğrudan aralıklara bölünmesi gerekiyor ya da gelir üzerindeki polinom regresyonunun etkin bir şekilde yapılabilmesi için daha yüksek gelir güçlerinin eklenmesi gerekiyor .

"Log-lineer" bir model olarak

Yine başka bir formülasyon, yukarıdaki iki yönlü gizli değişken formülasyonunu, gizli değişkenler olmadan daha yüksek orijinal formülasyonla birleştirir ve işlemde, çok terimli logitin standart formülasyonlarından birine bir bağlantı sağlar .

Burada, yerine yazma logit olasılıkları arasında p _i lineer tahmin unsuru olarak biz, iki, iki sonuç her biri için içine bir doğrusal tahmin ayrı:

${\displaystyle {\begin{hizalanmış}\ln \Pr(Y_{i}=0)&={\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}-\ln Z \\\ln \Pr(Y_{i}=1)&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}-\ln Z\end{hizalı}}}$

İki yönlü gizli değişken modelinde olduğu gibi iki ayrı regresyon katsayıları kümesinin tanıtıldığına ve iki denklemin , sonunda fazladan bir terimle birlikte doğrusal bir tahmin edici olarak ilişkili olasılığın logaritmasını yazan bir form olarak göründüğüne dikkat edin. . Bu terim, ortaya çıktığı gibi , sonucun bir dağılım olmasını sağlayan normalleştirici faktör olarak hizmet eder . Bu, her iki tarafı da üslendirerek görülebilir: ${\görüntüleme stili -\ln Z}$

${\displaystyle {\begin{hizalanmış}\Pr(Y_{i}=0)&={\frac {1}{Z}}e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}\\[5pt]\Pr(Y_{i}=1)&={\frac {1}{Z}}e^{{\boldsymbol {\beta }}_{1} \cdot \mathbf {X} _{i}}\end{hizalı}}}$

Bu formda, Z'nin amacının, Y _i üzerinden elde edilen dağılımın aslında bir olasılık dağılımı olmasını , yani toplamının 1 olmasını sağlamak olduğu açıktır . Bu, Z'nin basitçe tüm normalleştirilmemiş olasılıkların toplamı olduğu anlamına gelir ve her bir olasılığın Z'ye bölünmesiyle , olasılıklar " normalleştirilmiş " hale gelir . Yani:

${\displaystyle Z=e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}$

ve elde edilen denklemler

${\displaystyle {\begin{aligned}\Pr(Y_{i}=0)&={\frac {e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i }}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \ mathbf {X} _{i}}}}\\[5pt]\Pr(Y_{i}=1)&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \ mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }} _{1}\cdot \mathbf {X} _{i}}}}.\end{hizalı}}}$

Veya genel olarak:

${\displaystyle \Pr(Y_{i}=c)={\frac {e^{{\boldsymbol {\beta }}_{c}\cdot \mathbf {X} _{i}}}{\sum _ {h}e^{{\boldsymbol {\beta }}_{h}\cdot \mathbf {X} _{i}}}}}$

Bu, çok terimli logitte olduğu gibi, bu formülasyonun ikiden fazla sonuca nasıl genelleştirileceğini açıkça göstermektedir . Bu genel formülasyonun tam olarak aşağıdaki gibi softmax işlevi olduğuna dikkat edin .

${\displaystyle \Pr(Y_{i}=c)=\operatöradı {softmax} (c,{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i},{\boldsymbol { \beta }}_{1}\cdot \mathbf {X} _{i},\dots ).}$

Bunun önceki modele eşdeğer olduğunu kanıtlamak için, yukarıdaki modelin bu konuda gereğinden fazla belirtilmiş olduğunu ve bağımsız olarak belirlenemeyeceğini unutmayın: yani birini bilmek otomatik olarak diğerini belirler. Bunun bir sonucu olarak, model nonidentifiable bu çoklu kombinasyonlar, β ₀ ve β ₁ tüm olası açıklayıcı değişkenler aynı olasılıkları üretecektir. Aslında, her ikisine de herhangi bir sabit vektör eklenmesinin aynı olasılıkları üreteceği görülebilir: ${\displaystyle \Pr(Y_{i}=0)}$${\displaystyle \Pr(Y_{i}=1)}$${\displaystyle \Pr(Y_{i}=0)+\Pr(Y_{i}=1)=1}$

${\displaystyle {\begin{hizalanmış}\Pr(Y_{i}=1)&={\frac {e^{({\boldsymbol {\beta }}_{1}+\mathbf {C} )\cdot \mathbf {X} _{i}}}{e^{({\boldsymbol {\beta }}_{0}+\mathbf {C} )\cdot \mathbf {X} _{i}}+e^ {({\boldsymbol {\beta }}_{1}+\mathbf {C} )\cdot \mathbf {X} _{i}}}}\\[5pt]&={\frac {e^{{ \boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}}{e^{{\ boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}+e^{{\boldsymbol { \beta }}_{1}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}}}\\[5pt]&={ \frac {e^{\mathbf {C} \cdot \mathbf {X} _{i}}e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}} }{e^{\mathbf {C} \cdot \mathbf {X} _{i}}(e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}} +e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}})}}\\[5pt]&={\frac {e^{{\boldsymbol {\ beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e ^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}.\end{hizalı}} }$

Sonuç olarak, iki vektörden biri için keyfi bir değer seçerek meseleleri basitleştirebilir ve tanımlanabilirliği geri yükleyebiliriz. Sonra ayarlamayı seçiyoruz , ${\displaystyle {\boldsymbol {\beta }}_{0}=\mathbf {0} .}$

${\displaystyle e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}=e^{\mathbf {0} \cdot \mathbf {X} _{i} }=1}$

ve bu yüzden

${\displaystyle \Pr(Y_{i}=1)={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{1+e ^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}={\frac {1}{1+e^{-{\boldsymbol {\beta }} _{1}\cdot \mathbf {X} _{i}}}}=p_{i}}$

bu, bu formülasyonun gerçekten önceki formülasyona eşdeğer olduğunu gösterir. (İki yönlü gizli değişken formülasyonunda olduğu gibi , eşdeğer sonuçlar üretecek herhangi bir ayar .) ${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0}}$

Çok terimli logit modelin çoğu tedavisinin ya burada sunulan "log-doğrusal" formülasyonu ya da yukarıda sunulan iki yönlü gizli değişken formülasyonunu genişleterek başladığını unutmayın, çünkü her ikisi de modelin çok yönlü olarak genişletilebileceğini açıkça gösterir. sonuçlar. Genel olarak, gizli değişkenlerle sunum , ayrık seçim modellerinin ve fayda teorisinin hüküm sürdüğü ekonometri ve siyaset biliminde daha yaygındır , buradaki "log-lineer" formülasyon ise bilgisayar bilimlerinde , örneğin makine öğrenimi ve doğal dil işlemede daha yaygındır .

Tek katmanlı algılayıcı olarak

Modelin eşdeğer bir formülasyonu var

${\displaystyle p_{i}={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k) }x_{k,i})}}}.\,}$

Bu işlevsel forma genellikle tek katmanlı algılayıcı veya tek katmanlı yapay sinir ağı denir . Tek katmanlı bir sinir ağı, bir adım işlevi yerine sürekli bir çıktı hesaplar . Türevi p _I ile ilgili olarak , X  = ( x ₁ , ..., x _k ), genel biçimde hesaplanır:

${\displaystyle y={\frac {1}{1+e^{-f(X)}}}}$

burada f ( x ), bir bir analitik fonksiyon olarak X . Bu seçimle, tek katmanlı sinir ağı, lojistik regresyon modeliyle aynıdır. Bu fonksiyonun geri yayılımda kullanılmasına izin veren sürekli bir türevi vardır . Bu fonksiyon da türevi kolayca hesaplandığından tercih edilir:

${\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} X}}=y(1-y){\frac {\mathrm {d} f}{\mathrm {d} X}} .\,}$

Binom verileri açısından

Yakından ilişkili bir model, her bir i'nin tek bir Bernoulli denemesi ile değil, n _i bağımsız özdeş olarak dağıtılmış deneme ile ilişkili olduğunu varsayar , burada Y _i gözlemlenen başarıların sayısıdır (bireysel Bernoulli tarafından dağıtılan rastgele değişkenlerin toplamı) ve dolayısıyla bir binom dağılımı izler :

${\displaystyle Y_{i}\,\sim \operatöradı {Bin} (n_{i},p_{i}),{\text{ for }}i=1,\dots ,n}$

Bu dağılımın bir örneği, n _i ekildikten sonra filizlenen tohumların oranıdır ( p _i ) .

Beklenen değerler açısından bu model şu şekilde ifade edilir:

${\displaystyle p_{i}=\operatöradı {\mathcal {E}} \left[\left.{\frac {Y_{i}}{n_{i}}}\,\right|\,\mathbf {X } _{i}\sağ]\,,}$

Böylece

${\displaystyle \operatöradı {logit} \left(\operatöradı {\mathcal {E}} \sol[\left.{\frac {Y_{i}}{n_{i}}}\,\sağ|\,\ mathbf {X} _{i}\sağ]\sağ)=\operatöradı {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}} \sağ)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}\,,}$

Veya eşdeğer olarak:

${\displaystyle \Pr(Y_{i}=y\mid \mathbf {X} _{i})={n_{i} \y}p_{i}^{y}(1-p_{i}) seçin ^{n_{i}-y}={n_{i} \seç y}\left({\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\sağ)^{y}\left(1-{\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i }}}}\sağ)^{n_{i}-y}\,.}$

Bu model, yukarıdaki daha temel modelle aynı türden yöntemler kullanılarak sığdırılabilir.

Bayes

Bir Bayes istatistik bağlamında, önceki dağılımlar normal olarak, genellikle Gauss dağılımları biçiminde, regresyon katsayılarına yerleştirilir . Diye bir şey yok önceki konjuge ait olabilirlik fonksiyonu lojistik regresyon içinde. Bayes çıkarımı analitik olarak yapıldığında, bu , çok düşük boyutlar dışında sonsal dağılımın hesaplanmasını zorlaştırdı. Şimdi ise OpenBUGS , JAGS , PyMC3 , Stan veya Turing.jl gibi otomatik yazılımlar bu posteriorların simülasyon kullanılarak hesaplanmasına izin veriyor, bu nedenle konjugat eksikliği bir endişe değil. Ancak, örnek boyutu veya parametre sayısı büyük olduğunda, tam Bayes simülasyonu yavaş olabilir ve insanlar genellikle varyasyonel Bayes yöntemleri ve beklenti yayılımı gibi yaklaşık yöntemleri kullanır .

Tarih

Lojistik regresyonun ayrıntılı bir geçmişi Cramer (2002)'de verilmektedir . Lojistik işlev, nüfus artışının bir modeli olarak geliştirildi ve 1830'larda ve 1840'larda Adolphe Quetelet'in rehberliğinde Pierre François Verhulst tarafından "lojistik" olarak adlandırıldı ; bkz Lojistik fonksiyon § Geçmiş detaylar için. İlk makalesinde (1838), Verhulst eğrileri verilere nasıl uydurduğunu belirtmedi. Verhulst, daha ayrıntılı makalesinde (1845), eğrinin gözlemlenen üç noktadan geçmesini sağlayarak modelin üç parametresini belirledi ve bu da zayıf tahminler verdi.

Lojistik fonksiyon, kimyada bir otokataliz modeli olarak bağımsız olarak geliştirildi ( Wilhelm Ostwald , 1883). Bir otokatalitik reaksiyon, ürünlerden birinin kendisinin aynı reaksiyon için bir katalizör olduğu, reaktanlardan birinin arzının sabit olduğu bir reaksiyondur. Bu, doğal olarak, nüfus artışıyla aynı nedenden dolayı lojistik denklemin ortaya çıkmasına neden olur: Tepki kendi kendini güçlendirir ancak sınırlıdır.

Lojistik işlevi bağımsız olarak 1920'de Raymond Pearl ve Lowell Reed tarafından bir nüfus artışı modeli olarak yeniden keşfedildi , Pearl & Reed (1920) olarak yayınlandı ve modern istatistiklerde kullanılmasına yol açtı. Başlangıçta Verhulst'un çalışmasından habersizdiler ve muhtemelen bunu L. Gustave du Pasquier'den öğrendiler , ancak ona çok az kredi verdiler ve terminolojisini benimsemediler. Verhulst'un önceliği kabul edildi ve "lojistik" terimi 1925'te Udny Yule tarafından yeniden canlandırıldı ve o zamandan beri takip ediliyor . Pearl ve Reed, modeli ilk olarak Amerika Birleşik Devletleri nüfusuna uyguladılar ve ayrıca başlangıçta eğriyi üç noktadan geçirmesini sağlayarak uydurdular; Verhulst'ta olduğu gibi, bu da yine kötü sonuçlar verdi. harvtxt hatası: hedef yok: CITEREFPearlReed1920 ( yardım )

1930'larda, probit modeli geliştirildi ve sistematize Chester Ittner Bliss terimi "probit" terimini, Bliss (1934) , tarafından John Gaddum içinde Gaddum (1933) , ve model uyum maksimum olabilirlik tahmini tarafından Ronald A . Fisher içinde Fisher (1935) Bliss çalışmalarına bir ek olarak,. Probit modeli esas olarak biyo-tahlilde kullanıldı ve öncesinde 1860'a tarihlenen daha önceki çalışmalar vardı; bkz. Probit modeli § Geçmiş . Probit modeli, logit modelinin sonraki gelişimini etkilemiş ve bu modeller birbirleriyle rekabet etmiştir. harvtxt hatası: hedef yok: CITEREFBliss1934 ( yardım )harvtxt hatası: hedef yok: CITEREFGaddum1933 ( yardım )harvtxt hatası: hedef yok: CITEREFFisher1935 ( yardım )

Lojistik model muhtemelen ilk olarak Edwin Bidwell Wilson ve öğrencisi Jane Worcester tarafından Wilson & Worcester'da (1943) biyo-tahlilde probit modeline bir alternatif olarak kullanılmıştır . Bununla birlikte, lojistik modelin probit modeline genel bir alternatif olarak geliştirilmesi, esas olarak, Joseph Berkson'ın Berkson'dan (1944) başlayarak, "probit" ile benzer şekilde "logit"i icat ettiği on yıllar boyunca yaptığı çalışmalardan kaynaklanmaktadır. ve Berkson (1951) ve sonraki yıllarda devam etmektedir. Logit modeli başlangıçta probit modelinden daha düşük olduğu için reddedildi, ancak özellikle 1960 ve 1970 arasında "yavaş yavaş logit ile eşit bir temele ulaştı". 1970'e gelindiğinde, logit modeli istatistik dergilerinde ve sonrasında kullanımda olan probit modeliyle pariteye ulaştı. aştı. Bu göreceli popülerlik, probitin biyoassay içindeki yerini almaktan ziyade logitin biyoassay dışında benimsenmesi ve pratikte gayri resmi kullanımından kaynaklanmaktadır; logit'in popülaritesi, logit modelinin hesaplama basitliğine, matematiksel özelliklerine ve çeşitli alanlarda kullanımına izin veren genelliğine yatırılır. harvtxt hatası: hedef yok: CITEREFBerkson1944 ( yardım )harvtxt hatası: hedef yok: CITEREFBerkson1951 ( yardım )

Bu süre zarfında, Cox'ta (1958) olduğu gibi , özellikle David Cox tarafından çeşitli iyileştirmeler yapıldı .

Çok terimli logit modeli, Cox (1966) ve Thiel'de (1969) bağımsız olarak tanıtıldı , bu da logit modelinin uygulama kapsamını ve popülaritesini büyük ölçüde artırdı. 1973'te Daniel McFadden çok terimli logiti ayrık seçim teorisiyle , özellikle Luce'un seçim aksiyomuyla ilişkilendirerek , çok terimli logitin alakasız alternatiflerin bağımsızlığı varsayımından çıktığını ve alternatiflerin olasılıklarını göreceli tercihler olarak yorumladığını gösterdi; bu lojistik regresyon için teorik bir temel verdi.

Uzantılar

Çok sayıda uzantı var:

• Çok terimli lojistik regresyon (veya çok terimli logit ), çok yönlü kategorik bağımlı değişken (sırasız değerlerle, "sınıflandırma" olarak da adlandırılır ) durumunu ele alır . İkiden fazla değere sahip bağımlı değişkenlere sahip olmanın genel durumunun politomlu regresyon olarak adlandırıldığını unutmayın .
• Sıralı lojistik regresyon (veya sıralı logit ) sıralı bağımlı değişkenleri (sıralı değerler) işler .
• Karışık logit , bağımlı değişkenin seçimleri arasında korelasyonlara izin veren çok terimli logitin bir uzantısıdır.
• Lojistik modelin birbirine bağımlı değişken kümelerine bir uzantısı koşullu rastgele alandır .
• Koşullu lojistik regresyon , katmanlar küçük olduğunda eşleşen veya katmanlara ayrılmış verileri işler . Çoğunlukla gözlemsel çalışmaların analizinde kullanılır .

Yazılım

Çoğu istatistiksel yazılım ikili lojistik regresyon yapabilir.

• SPSS
  • [1] temel lojistik regresyon için.
• durum
• SAS
  • Temel lojistik regresyon için PROC LOJİSTİK .
  • PROC CATMOD tüm değişkenler kategorik olduğunda.
  • Çok seviyeli model lojistik regresyon için PROC GLIMMIX .
• r
  • glm istatistik paketinde (aile = binom kullanılarak)
  • lrmiçinde rms paketin
  • Verimli bir uygulama için GLMNET paketi düzenli lojistik regresyon
  • karışık etkiler lojistik regresyon için lmer
  • gm_logisticBüyük ölçekli verileri içeren hızlı ve ağır hesaplamalar için Rfast paket komutu .
  • bayesian lojistik regresyon için kol paketi
• piton
  • Logitiçinde Statsmodels modülü.
  • LogisticRegressioniçinde Scikit-öğrenme modülü.
  • LogisticRegressoriçinde TensorFlow modülü.
  • Theano eğitiminde tam lojistik regresyon örneği [2]
  • ARD ön kodu ile Bayes Lojistik Regresyon , öğretici
  • ARD ön kodu ile Varyasyonel Bayes Lojistik Regresyon , öğretici
  • Bayesian Lojistik Regresyon kodu , öğretici
• NCSS
  • NCSS'de Lojistik Regresyon
• matlab
  • mnrfitiçinde İstatistik ve Yapay Öğrenme Araç Kutusu ( "yanlış" 2 yerine 0 olarak kodlanmıştır ile)
  • fminunc/fmincon, fitglm, mnrfit, fitclinear, mle hepsi lojistik regresyon yapabilir.
• Java ( JVM )
  • LibLinear
  • Apache Flink'i
  • Apaçi Kıvılcımı
    • SparkML , Lojistik Regresyonu destekler
• FPGA
  • Logistic Regresesion IP coreiçinde HLS için FPGA .

Özellikle, Microsoft Excel'in istatistik uzantı paketi bunu içermez.

Ayrıca bakınız

• lojistik fonksiyon
• ayrık seçim
• Jarrow-Turnbull modeli
• Sınırlı bağımlı değişken
• Çok terimli logit modeli
• sıralı logit
• Hosmer-Lemeshow testi
• Brier puanı
• mlpack - lojistik regresyonun bir C++ uygulamasını içerir
• Yerel vaka kontrol örneklemesi
• Lojistik model ağacı

Referanslar

daha fazla okuma

Dış bağlantılar

• İlgili medya Lojistik regresyon Wikimedia Commons
• : Ekonometri Ders (Lojit modeli konu) üzerinde YouTube tarafından Mark Thoma
• Lojistik Regresyon öğreticisi
• mlelr : C dilinde öğretim amaçlı yazılım