1 + 2 + 3 + 4 + ⋯ - 1 + 2 + 3 + 4 + ⋯

Olan terimler sonsuz seriler olan doğal sayılar 1 + 2 + 3 + 4 + ⋯ a, ıraksak serisi . N, dizi kısmi toplamı th üçgen sayı

${\displaystyle \sum _{k=1}^{n}k={\frac {n(n+1)}{2}},}$

n sonsuza giderken sınırsız olarak artar . Çünkü dizi kısmi toplamlarının başarısız bir limit değere yakınsaması , seri bir miktar bulunmamaktadır.

Seri ilk bakışta anlamlı bir değere sahip değil gibi görünse de, matematiksel olarak ilginç bir dizi sonuç verecek şekilde manipüle edilebilir. Örneğin, matematikte ıraksak bir diziye bile sayısal değerler atamak için birçok toplama yöntemi kullanılır. Özellikle, zeta fonksiyonu düzenleme ve Ramanujan toplama yöntemleri, diziye ünlü bir formülle ifade edilen -1/12 değerini atar.

${\displaystyle 1+2+3+4+\cdots =-{\frac {1}{12}},}$

burada sol taraf, bilinen anlamıyla sonsuz bir serinin toplamı olarak değil, yukarıda belirtilen toplama yöntemlerinden biri kullanılarak elde edilen değer olarak yorumlanmalıdır . Bu yöntemlerin karmaşık analiz , kuantum alan teorisi ve sicim teorisi gibi diğer alanlarda uygulamaları vardır .

Moonshine teorisi üzerine bir monografide Terry Gannon, bu denklemi "bilimdeki en dikkat çekici formüllerden biri" olarak adlandırıyor.

Kısmi toplamlar

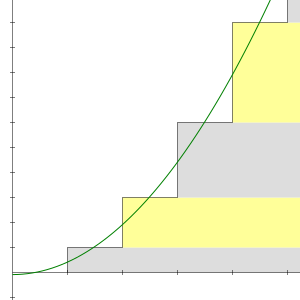
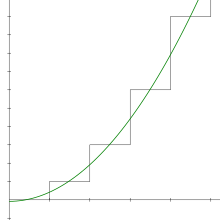
Dizi kısmi toplamları 1 + 2 + 3 + 4 + 5 + 6 + ⋯ olan 1, 3, 6, 10, 15 , vb N inci kısmi toplam basit bir formül ile verilir:

${\displaystyle \sum _{k=1}^{n}k={\frac {n(n+1)}{2}}.}$

Bu denklem Pisagorcular tarafından MÖ altıncı yüzyılda biliniyordu . Bu formun sayılarına üçgen sayılar denir , çünkü bunlar bir eşkenar üçgen olarak düzenlenebilmektedir.

Üçgen sayıların sonsuz dizisi +∞'ye ıraksar , dolayısıyla tanım gereği 1 + 2 + 3 + 4 + ⋯ sonsuz serisi de +∞'ye ıraksar. Sapma, dizinin biçiminin basit bir sonucudur: terimler sıfıra yaklaşmaz, bu nedenle seri, test terimiyle ıraksar .

toplanabilirlik

Klasik ıraksak seriler arasında 1 + 2 + 3 + 4 + ⋯' nin sonlu bir değere dönüştürülmesi nispeten zordur. Bazıları diğerlerinden daha güçlü olan farklı serilere sayısal değerler atamak için birçok toplama yöntemi kullanılır. Örneğin, cesàro toplaması iyi bilinen bir yöntem olduğu toplamları Grandi'nin serisi , hafif ıraksak serisi 1-1 + 1-1 + ⋯ için1/2. Abel toplamı , yalnızca Grandi'nin serilerini toplamakla kalmayıp, daha güçlü bir yöntemdir.1/2, aynı zamanda 1 − 2 + 3 − 4 + ⋯ arasındaki daha zor seriyi de toplar .1/4.

Yukarıdaki serilerden farklı olarak, 1 + 2 + 3 + 4 + ⋯ , Cesàro toplanabilir veya Abel toplanabilir değildir. Bu yöntemler salınımlı ıraksak seriler üzerinde çalışır, ancak +∞'ye ıraksayan bir seri için sonlu bir cevap üretemezler. Iraksak bir serinin toplamının daha temel tanımlarının çoğu kararlı ve doğrusaldır ve hem kararlı hem de doğrusal olan herhangi bir yöntem 1 + 2 + 3 + ⋯' yi sonlu bir değere toplayamaz ; aşağıya bakınız. Zeta işlevi düzenlemesi veya Ramanujan toplamı gibi daha gelişmiş yöntemler gereklidir . Değeri için tartışmak da mümkündür -+1/12 bu yöntemlerle ilgili bazı kaba buluşsal yöntemlerin kullanılması.

Sezgisel

Srinivasa Ramanujan , " 1 + 2 + 3 + 4 + ⋯ = − ifadesinin iki türevini sundu.+1/12" ilk defterinin 8. bölümünde. Daha basit, daha az titiz olan türetme aşağıdaki gibi iki adımda ilerler.

İlk temel kavrayış, 1 + 2 + 3 + 4 + ⋯ pozitif sayılar dizisinin, 1 − 2 + 3 − 4 + ⋯ dönüşümlü serisine çok benzediğidir . İkinci seri de farklıdır, ancak onunla çalışmak çok daha kolaydır; ona bir değer veren ve 18. yüzyıldan beri araştırılan birkaç klasik yöntem vardır.

Seri dönüşümü için 1 + 2 + 3 + 4 + ⋯ içine 3 + 12-4 + ⋯ , altıda bir dönem dördüncü dönem, 12 ikinci dönem, 8'den 4 çıkarma ve benzeri olabilir . Toplam çıkarılacak miktar 4 + 8 + 12 + 16 + ⋯ yani orijinal dizinin 4 katıdır. Bu ilişkiler cebir kullanılarak ifade edilebilir. Serinin "toplamı" ne olursa olsun, onu c = 1 + 2 + 3 + 4 + ⋯ olarak adlandırın. Sonra bu denklemi 4 ile çarpın ve ikinci denklemi birinciden çıkarın:

${\displaystyle {\begin{alignedat}{7}c={}&&1+2&&{}+3+4&&{}+5+6+\cdots \\4c={}&&4&&{}+8&&{}+12+ \cdots \\c-4c={}&&1-2&&{}+3-4&&{}+5-6+\cdots \end{alignedat}}}$

İkinci temel anlayış, 1 − 2 + 3 − 4 + ⋯ değişken serisinin , fonksiyonun formel kuvvet serisi açılımı olduğudur .1/(1 + x ) ²ancak x 1 olarak tanımlanır. Buna göre Ramanujan şöyle yazar

${\displaystyle -3c=1-2+3-4+\cdots ={\frac {1}{(1+1)^{2}}}={\frac {1}{4}}.}$

Her iki tarafı -3'e bölerek c  =  − elde edilir.+1/12.

Genel olarak konuşursak, sonsuz serileri sonlu toplamlarmış gibi manipüle etmek yanlıştır. Örneğin, ıraksak bir serinin rastgele konumlarına sıfırlar eklenirse, diğer yöntemlerle tutarlı olmak şöyle dursun, kendi içinde tutarlı olmayan sonuçlara ulaşmak mümkündür. Özellikle, 4 c = 0 + 4 + 0 + 8 + ⋯ adımı , yalnızca toplamsal özdeşlik yasasıyla doğrulanmaz . Uç bir örnek için, dizinin önüne tek bir sıfır eklemek farklı bir sonuca yol açabilir.

Bu durumu düzeltmenin ve sıfırların eklenebileceği yerleri sınırlamanın bir yolu, bir fonksiyona bağımlılık ekleyerek dizideki her bir terimi takip etmektir. Seri 1 + 2 + 3 + 4 + ⋯ her terim n sadece bir sayıdır. n terimi , s'nin karmaşık bir değişken olduğu n ^−s işlevine yükseltilirse , yalnızca benzer terimlerin eklenmesi sağlanabilir. Ortaya çıkan seri daha sıkı bir şekilde manipüle edilebilir ve s değişkeni daha sonra -1 olarak ayarlanabilir. Bu stratejinin uygulanmasına zeta fonksiyon düzenlemesi denir .

Zeta fonksiyon düzenlemesi

Gelen zeta fonksiyonu regularization , dizi dizi ile değiştirilir . Son seri Dirichlet serisinin bir örneğidir . s'nin reel kısmı 1'den büyük olduğunda, Dirichlet serisi yakınsar ve toplamı Riemann zeta fonksiyonu ζ ( s ) olur. Öte yandan, Dirichlet serisi, s'nin gerçek kısmı 1'den küçük veya ona eşit olduğunda ıraksar , bu nedenle, özellikle, s = –1 ayarından kaynaklanan 1 + 2 + 3 + 4 + ⋯ serisi yakınsamaz. . Riemann zeta fonksiyonu sokulması yararı diğer değerleri için tanımlanabilir olduğunu s ile analitik devamında . Bir sonra zeta-regularized toplamı tanımlayabilir 1 + 2 + 3 + 4 + ⋯ olduğu ζ (1). ${\textstyle \sum _{n=1}^{\infty}n}$${\textstyle \sum _{n=1}^{\infty}n^{-s}}$

Bu noktadan hareketle, ζ (−1) = − olduğunu kanıtlamanın birkaç yolu vardır.+1/12. Euler'in akıl yürütme çizgileri boyunca bir yöntem, Riemann zeta işlevi ile Dirichlet eta işlevi η ( s ) arasındaki ilişkiyi kullanır . eta işlevi, değişen bir Dirichlet serisi tarafından tanımlanır, bu nedenle bu yöntem daha önceki buluşsal yöntemlere paraleldir. Her iki Dirichlet serisinin yakınsadığı yerde, birinin özdeşlikleri vardır:

${\displaystyle {\begin{alignedat}{7}\zeta(s)&{}={}&1^{-s}+2^{-s}&&{}+3^{-s}+4^{ -s}&&{}+5^{-s}+6^{-s}+\cdots &\\2\times 2^{-s}\zeta(s)&{}={}&2\times 2 ^{-s}&&{}+2\times 4^{-s}&&{}+2\times 6^{-s}+\cdots &\\\left(1-2^{1-s}\ sağ)\zeta(s)&{}={}&1^{-s}-2^{-s}&&{}+3^{-s}-4^{-s}&&{}+5^{ -s}-6^{-s}+\cdots &=\eta (s).\end{alignedat}}}$

Her iki fonksiyon da analitik süreklilik ile yukarıdaki serilerin birbirinden ayrıldığı s değerlerini içerecek şekilde genişletildiğinde, özdeşlik korunmaya devam eder . İkame s = -1 , tek bir alır -3 ζ (1) = η (1). Şimdi, eta fonksiyonu, tek taraflı bir limit olan tanımlayıcı serilerinin Abel toplamına eşit olduğundan, η (−1) hesaplaması daha kolay bir iştir : ${\displaystyle (1-2^{1-s})\zeta(lar)=\eta(lar)}$

${\displaystyle -3\zeta (-1)=\eta (-1)=\lim _{x\to 1^{-}}\left(1-2x+3x^{2}-4x^{3} +\cdots \right)=\lim _{x\to 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}. }$

Her iki tarafı -3'e bölerek ζ (−1) = − elde edilir.+1/12.

Kesinti düzenlemesi

Bir kesme işlevi kullanarak düzenlileştirme yöntemi , seriyi ulaşacak şekilde "pürüzsüzleştirebilir" -+1/12. Yumuşatma, karmaşık analize dayanan zeta fonksiyonu düzenlemesi ile Euler-Maclaurin formülüne kısayolu olan Ramanujan toplamı arasında kavramsal bir köprüdür . Bunun yerine, yöntem, gerçek analizden yöntemler kullanarak, doğrudan serinin konservatif dönüşümleri üzerinde çalışır .

Buradaki fikir, kötü davranan ayrık serileri düzleştirilmiş bir sürümle değiştirmektir. ${\displaystyle \textstyle \sum _{n=0}^{N}n}$

${\displaystyle \sum _{n=0}^{\infty }nf\left({\frac {n}{N}}\sağ),}$

burada f , uygun özelliklere sahip bir kesme işlevidir. Kesme fonksiyonu f (0) = 1 olarak normalleştirilmelidir ; bu, diferansiyel denklemlerde kullanılandan farklı bir normalizasyondur. Cutoff işlevi, serideki kırışıklıkları yumuşatmak için yeterli sınırlı türevlere sahip olmalı ve serinin büyümesinden daha hızlı 0'a düşmelidir. Kolaylık sağlamak için, tek bir gerektirebilir f olan düz , sınırlı ve kompakt bir desteklenir . Bir zaman bu düzeltilmiş toplamıdır kanıtlayabilirim asimptotik için -+1/12+ CN ² , burada C , f'ye bağlı bir sabittir . Asimptotik genişlemenin sabit terimi f'ye bağlı değildir : analitik süreklilik tarafından verilen değerin aynı olması gerekir,  -+1/12.

Ramanujan toplamı

Ramanujan toplamı ve 1 + 2 + 3 + 4 + ⋯ da  -+1/12. Ramanujan, GH Hardy'ye yazdığı 27 Şubat 1913 tarihli ikinci mektubunda şunları yazdı :

"Sevgili Efendim, ben çok hangi Londra'da bir Matematik Profesörü dikkatlice incelemek için bana soran yazdı ben benzer sizden bir yanıt bekliyordum Şubat 1913. 8 mektubunuzu incelerken üzerinde gratified am Bromwich 'ın Sonsuz Serisi düşmek değil ... ona dizinin sonsuz sayıdaki terimlerinin toplamının: 1 + 2 + 3 + 4 + ⋯ = −+1/12benim teorim altında. Bunu size söylersem, hemen bana akıl hastanesini hedefim olarak göstereceksiniz. Üzerinde ilerlediğim satırları tek bir harfle belirtirsem, ispat yöntemlerimi izleyemeyeceğinize sizi ikna etmek için bu konuyu genişletiyorum. …"

Ramanujan toplamı, bir serinin kısmi toplamları için Euler-Maclaurin formülündeki sabit terimi ayırma yöntemidir . f fonksiyonu için, serinin klasik Ramanujan toplamı şu şekilde tanımlanır: ${\displaystyle \textstyle \sum _{k=1}^{\infty }f(k)}$

${\displaystyle c=-{\frac {1}{2}}f(0)-\sum _{k=1}^{\infty }{\frac {B_{2k}}{(2k)!}} f^{(2k-1)}(0),}$

burada f ^{(2 k -1)} (2 k  - 1) arasında inci türevi f ve B _{2 k} 2 k inci Bernoulli sayısı : B ₂ =1/6, B ₄ = -+1/30, ve bunun gibi. f ( x ) = x ayarı yapıldığında, f'nin birinci türevi 1'dir ve diğer tüm terimler yok olur, yani

${\displaystyle c=-{\frac {1}{6}}\times {\frac {1}{2!}}=-{\frac {1}{12}}.}$

Önlemek tutarsızlıklara Ramanujan toplamı modern teorisi gerektirir f yüksek dereceden türevleri anlamında "normal" bir ön 0 Ramanujan zımnen bu kabul Euler-Maclaurın formülde kalan terimler için yeterince hızlı bir şekilde bozunması eğilimi Emlak. Düzenlilik gereksinimi, 0 + 2 + 0 + 4 + ⋯ gibi aralıklı seriler üzerinde Ramanujan toplamının kullanılmasını engeller , çünkü hiçbir normal işlev bu değerleri almaz . Bunun yerine, böyle bir seri, zeta fonksiyonu düzenlemesi ile yorumlanmalıdır. Bu nedenle, Hardy, ilgili serilerin toplamlarını bulmak için bilinen serilerin Ramanujan toplamlarını uygularken "çok dikkatli" olmasını önerir.

Kararlı doğrusal toplama yöntemlerinin başarısızlığı

Bir toplamıdır yöntem doğrusal ve kararlı serisi Özetle olamaz 1 + 2 + 3 + ⋯ için bir sonlu değer. (Durağan, dizinin başına bir terim eklenmesinin toplamı aynı miktarda artırması anlamına gelir.) Bu durum aşağıdaki gibi görülebilir. Eğer

1 + 2 + 3 + ⋯ = x

sonra her iki tarafa 0 eklemek verir

0 + 1 + 2 + ⋯ = 0 + x = x

istikrar tarafından. Doğrusallıkla, birinci denklemden ikinci denklem çıkarılabilir (sütunlardaki ilk satırdan ikinci satırın her bir bileşeni çıkarılarak)

1 + 1 + 1 + ⋯ = x − x = 0.

Her iki tarafa da 0 eklemek tekrar verir

0 + 1 + 1 + 1 + ⋯ = 0,

ve son iki seriyi çıkarmak verir

1 + 0 + 0 + ⋯ = 0,

çelişkili istikrar

Bu nedenle, 1 + 2 + 3 + ⋯ toplamına sonlu bir değer veren her yöntem kararlı veya doğrusal değildir.

Fizik

Gelen bozonik sicim teorisi , girişim olası enerji bir dize seviyelerini, özellikle, en düşük enerji düzeyi hesaplamak etmektir. Gayri resmi olarak konuşursak, dizenin her harmoniği, D' nin uzay-zamanın boyutu olduğu, her enine yön için bir tane olmak üzere , D  -2 bağımsız kuantum harmonik osilatörlerin bir koleksiyonu olarak görülebilir . Temel salınım frekansı ise ω , bir osilatör sonra enerji katkıda n -inci harmonik nħω / 2. Yani ıraksak seriyi kullanarak, tüm harmoniklerin toplamı − ħω ( D − 2)/24 . Nihai olarak, Goddard-Thorn teoremi ile birleştiğinde , bozonik sicim teorisinin 26'dan başka boyutlarda tutarlı olamamasına yol açan bu gerçektir .

Düzgünleştirilmesi 1 + 2 + 3 + 4 + ⋯ da işlem katılır Casimir kuvveti bir için sayısal alanda tek boyutlu olarak. Üstel bir kesme işlevi, seriyi yumuşatmak için yeterlidir; bu, keyfi olarak yüksek enerji modlarının iletken plakalar tarafından engellenmediği gerçeğini temsil eder. Problemin uzaysal simetrisi, genişlemenin ikinci dereceden terimini iptal etmekten sorumludur. Geriye kalan tek şey -1/12 sabit terimidir ve bu sonucun negatif işareti Casimir kuvvetinin çekici olduğu gerçeğini yansıtır.

Benzer bir hesaplama, Riemann zeta işlevi yerine Epstein zeta işlevi kullanılarak üç boyutta yapılır .

Tarih

Leonhard Euler'in seriyi şu şekilde toplayıp toplamadığı belli değil -+1/12. Morris Kline'a göre , Euler'in ıraksak seriler üzerindeki ilk çalışması, 1 + 2 + 3 + 4 + ⋯ = ∞ sonucunu çıkardığı fonksiyon açılımlarına dayanıyordu . Raymond Ayoub'a göre ıraksak zeta serisinin Abel-toplanabilir olmaması, Euler'in zeta fonksiyonunu eta fonksiyonu kadar özgürce kullanmasını engelledi ve diziye "bir anlam yükleyemedi". Diğer yazarlar toplamı ile Euler'e kredi verdiler, bu da Euler'in zeta ve eta fonksiyonları arasındaki ilişkiyi negatif tamsayılara genişleteceğini öne sürdü. Birincil literatürde, 1 + 2 + 3 + 4 + ⋯ serisi , Euler'in 1760 yayını De seriebus divergentibus'ta 1 + 2 + 4 + 8 + ⋯ ıraksak geometrik serisinin yanında bahsedilmiştir . Euler, bu tür serilerin sonlu, negatif toplamları olduğunu ima eder ve bunun geometrik seriler için ne anlama geldiğini açıklar, ancak 1 + 2 + 3 + 4 + ⋯ tartışmasına geri dönmez . Aynı yayında Euler, 1 + 1 + 1 + 1 + ⋯ toplamının sonsuz olduğunu yazar.

popüler medyada

David Leavitt'in 2007 tarihli The Indian Clerk adlı romanı , Hardy ve Littlewood'un bu dizinin anlamını tartıştığı bir sahne içeriyor . Ramanujan'ın ζ (-1) 'i yeniden keşfettiği sonucuna varırlar ve ikinci mektubundaki "deli sığınma" satırını Ramanujan'ın kendileriyle oynadığının bir işareti olarak alırlar.

Simon McBurney'nin 2007 tarihli oyunu Bir Kaybolan Sayı , açılış sahnesinde diziye odaklanıyor. Ana karakter Ruth, bir konferans salonuna girer ve "Size gerçekten heyecan verici bir şey göstereceğim", yani 1 + 2 + 3 + 4 + ⋯ = − ilan etmeden önce farklı bir dizi fikrini sunar.+1/12. Ruth, zeta fonksiyonunun işlevsel denkleminin bir türevini başlatırken, başka bir aktör seyirciye seslenir ve onların aktör olduklarını kabul eder: "Ama matematik gerçektir. Korkunç ama gerçek."

Ocak 2014'te Numberphile , ilk ayında 1,5 milyondan fazla görüntülenen diziyle ilgili bir YouTube videosu hazırladı. 8 dakikalık video Nottingham Üniversitesi'nde fizikçi olan Tony Padilla tarafından anlatılıyor . Padilla 1 − 1 + 1 − 1 + ⋯ ve 1 − 2 + 3 − 4 + ⋯ ile başlar ve ikincisini Ramanujan'ın argümanına benzer bir terim terim çıkarma kullanarak 1 + 2 + 3 + 4 + ⋯ ile ilişkilendirir . Numberphile ayrıca 1 − 2 + 3 − 4 + ⋯ = nasıl daha ayrıntılı olarak açıklayan Nottingham fizikçisi Ed Copeland'ın yer aldığı videonun 21 dakikalık bir versiyonunu yayınladı.1/4Abel toplamı olarak ve 1 + 2 + 3 + 4 + ⋯ = −+1/12olarak Ç (1). Padilla, ilk videodaki titizlik eksikliği ile ilgili şikayetler aldıktan sonra, videodaki manipülasyonlarla ilgili Dirichlet serisinin analitik devamları arasındaki kimliklerle ilgili bir açıklama da kendi web sitesinde yazdı.

In New York Times, Numberphile videonun kapsama, matematikçi Edward Frenkel yorumladı: "Bu hesaplama matematik en iyi saklanan sırlarından biridir Hayır dış kimse bunu biliyor.".

Smithsonian dergisinde bu konunun kapsamı , Numberphile videosunu yanıltıcı olarak tanımlıyor ve toplamın şu şekilde yorumlandığını belirtiyor :+1/12eşittir araçlarının ilişkili olduğu analitik devamlılık tekniklerinden , eşittir işareti için özel bir anlama dayanır .

Referanslar

bibliyografya

daha fazla okuma

Dış bağlantılar

• Kuzu E. (2014), " 1+2+3… Gerçekten Eşit mi –1/12? ", Scientific American Blogs.
• Matematiksel Fizikte Bu Haftanın Buluntuları (124. Hafta , (126. Hafta) , (147. Hafta) , (213. Hafta)
  • Euler'in Kanıtı 1 + 2 + 3 + ⋯ = -1/12 – John Baez tarafından
  • John Baez (19 Eylül 2008). "Favori Numaralarım: 24" (PDF) .
• Euler-Maclaurin formülü, Bernoulli sayıları, zeta fonksiyonu ve Terence Tao tarafından gerçek değişken analitik devamı
• Luboš Motl tarafından negatif tam sayıların zetasının yinelemeli bir değerlendirmesi
• Numberphile videosuna bağlantı 1 + 2 + 3 + 4 + 5 + ... = –1/12
  • Doğal Sayıların Toplamı (ikinci kanıt ve ekstra görüntü) , Euler yönteminin gösterimini içerir.
  • Tüm doğal sayıları toplarsak ne elde ederiz? Tony Padilla tarafından video hakkındaki yorumlara yanıt
  • New York Times'tan ilgili makale
  • Neden –1/12 Edward Frenkel ile altın külçe takip Numberphile videosudur
• Iraksak Seriler: Neden 1 + 2 + 3 + ⋯ = −1/12 Arizona Üniversitesi'nden Brydon Cais