Laplace matrisi - Laplacian matrix

Olarak matematiksel alanında grafik teorisi , Laplace matris olarak da adlandırılır, grafik Laplace , admitans matrisi , Kirchhoff matrisi ya da ayrık Laplacian'ın , a, matris bir temsili grafiği . Laplacian matrisi, bir grafiğin birçok yararlı özelliğini bulmak için kullanılabilir. Kirchhoff teoremi ile birlikte, verilen bir grafik için yayılan ağaçların sayısını hesaplamak için kullanılabilir . Bir grafiğin en seyrek kesimi , Cheeger eşitsizliği ile Laplacian'ın ikinci en küçük öz değeri aracılığıyla yaklaşık olarak tahmin edilebilir . Ayrıca, çeşitli makine öğrenimi uygulamaları için faydalı olabilecek düşük boyutlu yerleştirmeler oluşturmak için de kullanılabilir.

Tanım

Basit grafikler için Laplace matrisi

Bir verilen basit bir grafik olan köşe, onun Laplace matris olarak tanımlanır: ${\görüntüleme stili G}$${\görüntüleme stili n}$${\textstyle L_{n\times n}}$

${\görüntüleme stili L=DA,}$

burada D , derece matrisidir ve A , grafiğin komşuluk matrisidir . İtibaren basit bir grafiktir, ancak 1 veya 0 içerir ve çapraz elemanlar her 0s. ${\metin stili G}$${\metin stili A}$

Halinde yönlendirilmiş grafikler , ya alıcılık veya outdegree uygulamaya bağlı olarak, kullanılabilir.

elemanları tarafından verilir ${\metin stili L}$

${\displaystyle L_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j\\-1&{\mbox{if}}\ i \neq j\ {\mbox{and}}\ v_{i}{\mbox{, }}v_{j}\\0&{\mbox{aksi halde}}\end{cases}}} ile bitişiktir$

tepe noktasının derecesi nerede . ${\displaystyle \operatöradı {derece} (v_{i})}$${\görüntüleme stili ben}$

Simetrik normalleştirilmiş Laplacian

Simetrik normalleştirilmiş Laplacian matrisi şu şekilde tanımlanır:

${\displaystyle L^{\text{sym}}:=D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}=ID^{-{ \frac {1}{2}}}REKLAM^{-{\frac {1}{2}}}}$,

elemanları tarafından verilir ${\textstyle L^{\text{sym}}}$

${\displaystyle L_{i,j}^{\text{sym}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ ve }}\deg(v_{i} )\neq 0\\-{\frac {1}{\sqrt {\deg(v_{i})\deg(v_{j})}}}&{\mbox{if }}i\neq j{\ mbox{ ve }}v_{i}{\mbox{, }}v_{j}\\0&{\mbox{aksi halde}} ile bitişiktir.\end{cases}}}$

Rastgele yürüyüş normalleştirilmiş Laplacian

Rastgele yürüyüşle normalize edilmiş Laplacian matrisi şu şekilde tanımlanır:

${\displaystyle L^{\text{rw}}:=D^{-1}L=ID^{-1}A}$

elemanları tarafından verilir ${\textstyle L^{\text{rw}}}$

${\displaystyle L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ ve }}\deg(v_{i} )\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if }}i\neq j{\mbox{ ve }}v_{i}{\mbox {, }}v_{j}\\0&{\mbox{aksi halde}} ile bitişiktir.\end{durumlar}}}$

Genelleştirilmiş Laplace

Genelleştirilmiş Laplacian şu şekilde tanımlanır: ${\görüntüleme stili Q}$

${\displaystyle {\begin{cases}Q_{i,j}<0&{\mbox{if }}i\neq j{\mbox{ ve }}v_{i}{\mbox{, }}v_{ ile bitişiktir j}\\Q_{i,j}=0&{\mbox{if }}i\neq j{\mbox{ ve }}v_{i}{\mbox{ }}v_{j}\\ ile bitişik değil {\mbox{herhangi bir sayı}}&{\mbox{aksi halde}}.\end{cases}}}$

Sıradan Laplacian'ın genelleştirilmiş bir Laplacian olduğuna dikkat edin.

Örnek

İşte etiketli, yönsüz bir grafiğin basit bir örneği ve Laplacian matrisi.

etiketli grafik	Derece matrisi	komşuluk matrisi	Laplace matrisi
	${\textstyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0\end}}$	${\textstyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&1&0\end}{\0&1&0&}}$	${\textstyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0& -1&3&0\\0&0&0&-1&0&1\\\end{dizi}}\sağ)}$

Özellikler

Bir (yönsüz) grafiği G ve özdeğerleri olan Laplacian matrisi L için : ${\textstyle \lambda _{0}\leq \lambda _{1}\leq \cdots \leq \lambda _{n-1}}$

• L olan simetrik .
• L bir pozitif yarı kesin (olup hepsi için ). Bu, insidans matrisi bölümünde (aşağıda) doğrulanmıştır . Bu aynı zamanda Laplacian'ın simetrik ve diyagonal olarak baskın olmasından da anlaşılabilir .${\textstyle \lambda _{i}\geq 0}$${\metin stili ben}$
• L bir M matrisidir (köşegen dışı girişleri pozitif değildir, ancak özdeğerlerinin gerçek kısımları negatif değildir).
• L' nin her satır toplamı ve sütun toplamı sıfırdır. Aslında, toplamda, tepe noktasının derecesi her komşu için "-1" ile toplanır.
• Sonuç olarak, , çünkü vektör tatmin eder Bu aynı zamanda Laplacian matrisinin tekil olduğu anlamına gelir.${\textstyle \lambda _{0}=0}$${\textstyle \mathbf {v} _{0}=(1,1,\noktalar,1)}$${\textstyle L\mathbf {v} _{0}=\mathbf {0} .}$
• Grafikteki bağlı bileşenlerin sayısı , Laplacian'ın sıfır uzayının boyutu ve 0 özdeğerinin cebirsel çokluğudur .
• L' nin sıfır olmayan en küçük özdeğerine spektral boşluk denir .
• L' nin ikinci en küçük öz değeri (sıfır olabilir ), G'nin cebirsel bağlanabilirliğidir (veya Fiedler değeridir ) ve bir grafiğin en seyrek kesimine yaklaşır .
• Laplace fonksiyonları n-boyutlu vektör alan bir operatör olduğu , G'nin tepe dizi ve .${\textstyle f:V\to \mathbb {R} }$${\metin stili V}$${\textstyle n=|V|}$
• G k-düzenli olduğunda, normalleştirilmiş Laplacian: , burada A komşuluk matrisidir ve I bir birim matrisidir.${\textstyle {\mathcal {L}}={\tfrac {1}{k}}L=I-{\tfrac {1}{k}}A}$
• Birden çok bağlı bileşene sahip bir grafik için , L bir blok diyagonal matrisidir, burada her blok, muhtemelen köşeleri yeniden sıraladıktan sonra (yani L , bir blok köşegen matrisine benzer bir permütasyondur) her bileşen için ilgili Laplacian matrisidir .
• Laplacian matris L' nin izi , dikkate alınan grafiğin kenar sayısının nerede olduğuna eşittir .${\metin stili 2m}$${\metin stili m}$

insidans matrisi

Bir tanımlama yönlendirilmiş sıklığı matris M elemanı ile M _EV kenarı için e (köşe bağlantı i ve j ile, i  >  j ) ve tepe noktası V ile verilen ${\textstyle |e|\kez |v|}$

${\displaystyle M_{ev}=\left\{{\begin{array}{rl}1,&{\text{if }}v=i\\-1,&{\text{if }}v=j \\0,&{\text{aksi halde}}.\end{dizi}}\sağ.}$

O zaman Laplacian matrisi L tatmin eder

${\displaystyle L=M^{\textsf {T}}M}$

burada bir matris devrik ait M . ${\textstyle M^{\textsf {T}}}$

Şimdi , birim norm özvektörleri ve karşılık gelen özdeğerleri olan bir özbileşimini düşünün : ${\metin stili L}$${\textstyle \mathbf {v} _{i}}$${\textstyle \lambda _{i}}$

${\displaystyle {\begin{hizalanmış}\lambda _{i}&=\mathbf {v} _{i}^{\textsf {T}}L\mathbf {v} _{i}\\&=\mathbf {v} _{i}^{\textsf {T}}M^{\textsf {T}}M\mathbf {v} _{i}\\&=\left(M\mathbf {v} _{i }\sağ)^{\textsf {T}}\left(M\mathbf {v} _{i}\sağ).\\\end{hizalı}}}$

Çünkü vektör iç ürün olarak yazılabilir kendisi ile, bu görüntüler ve özdeğerler böylece her sigara negatiftir. ${\textstyle \lambda _{i}}$${\textstyle M\mathbf {v} _{i}}$${\textstyle \lambda _{i}\geq 0}$${\metin stili L}$

Deforme Laplacian

Deforme Laplace genel olarak tanımlanmaktadır

${\displaystyle \Delta(lar)=I-sA+s^{2}(DI)}$

burada I birim matris, A komşuluk matrisi, D derece matrisi ve s (karmaşık değerli) bir sayıdır.
Standart Laplace adildir ve signless Laplace olduğunu. ${\textstyle \Delta (1)}$${\textstyle \Delta (-1)=D+A}$

İşaretsiz Laplacian

Laplace signless olarak tanımlanır

${\görüntüleme stili Q=D+A}$

derece matrisi nerede ve komşuluk matrisi. İşaretli Laplace gibi, işaretsiz Laplacian da pozitif yarı tanımlıdır , çünkü şu şekilde çarpanlarına ayrılabilir: ${\görüntüleme stili D}$${\görüntüleme stili A}$${\görüntüleme stili L}$${\görüntüleme stili Q}$

${\displaystyle Q=RR^{\textsf {T}}}$

insidans matrisi nerede . 0 özvektöre sahiptir, ancak ve ancak izole köşeler dışında iki parçalı bağlantılı bir bileşene sahipse. Bu şu şekilde gösterilebilir ${\metin stili R}$${\görüntüleme stili Q}$

${\displaystyle \mathbf {x} ^{\textsf {T}}Q\mathbf {x} =\mathbf {x} ^{\textsf {T}}RR^{\textsf {T}}\mathbf {x} \R^{\textsf {T}}\mathbf {x} =\mathbf {0} .} anlamına gelir$

Bunun, yalnızca grafiğin iki parçalı bağlantılı bir bileşeni varsa ve varsa bir çözümü vardır. ${\displaystyle \mathbf {x} \neq \mathbf {0} }$

Simetrik normalleştirilmiş Laplacian

(Simetrik) Laplace normalize olarak tanımlanır

${\displaystyle L^{\text{sym}}:=D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}=ID^{-{ \frac {1}{2}}}REKLAM^{-{\frac {1}{2}}}}$

burada L (normalleştirilmemiş) Laplacian'dır, A komşuluk matrisidir ve D derece matrisidir. D derece matrisi köşegen ve pozitif olduğundan, bunun karşılıklı karekökü sadece köşegen girişleri D' nin köşegen girişlerinin pozitif kareköklerinin tersi olan köşegen matristir . Simetrik normalleştirilmiş Laplacian, simetrik bir matristir. ${\textstyle D^{-{\frac {1}{2}}}}$

Birinde: , burada S, satırları köşeler tarafından indekslenen ve sütunları G'nin kenarları tarafından indekslenen matristir, öyle ki her sütun bir e = {u, v} kenarına karşılık gelen satırda u'ya karşılık gelen bir girişe sahiptir. , satırda v'ye karşılık gelen bir giriş ve başka bir yerde 0 girişi var. ( S'nin devriğini gösterir). ${\textstyle L^{\text{sym}}=SS^{*}}$${\textstyle {\frac {1}{\sqrt {d_{u}}}}}$${\textstyle -{\frac {1}{\sqrt {d_{v}}}}}$${\textstyle S^{*}}$

Normalleştirilmiş Laplacian'ın tüm özdeğerleri reeldir ve negatif değildir. Bunu aşağıdaki gibi görebiliriz. Yana simetrik ise, kendi öz değerleri gerçek. Ayrıca negatif değildirler: özdeğeri λ olan bir özvektör düşünün ve varsayalım . (g ve f'yi v köşelerinde gerçek fonksiyonlar olarak kabul edebiliriz.) Sonra: ${\textstyle L^{\text{sym}}}$${\metin stili g}$${\textstyle L^{\text{sym}}}$${\textstyle g=D^{\frac {1}{2}}f}$

${\displaystyle \lambda \ =\ {\frac {\langle g,L^{\text{sym}}g\rangle }{\langle g,g\rangle }}\ =\ {\frac {\sol\langle g,D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}g\right\rangle }{\langle g,g\rangle }}\ = \ {\frac {\langle f,Lf\rangle }{\left\langle D^{\frac {1}{2}}f,D^{\frac {1}{2}}f\right\rangle } }\ =\ {\frac {\sum _{u\sim v}(f(u)-f(v))^{2}}{\sum _{v}f(v)^{2}d_{ v}}}\ \geq \ 0,}$

iç çarpımı kullandığımız yerde , tüm v köşelerinin toplamıdır ve {u,v} tüm sırasız köşe çiftlerinin toplamını gösterir. Miktar olarak adlandırılır Dirichlet toplamı sentezleme ise, f denir Rayleigh bölüm g. ${\textstyle \langle f,g\rangle =\sum _{v}f(v)g(v)}$${\textstyle \sum _{u\sim v}}$${\textstyle \sum _{u,v}(f(u)-f(v))^{2}}$${\textstyle {\frac {\left\langle g,L^{\text{sym}}g\right\rangle }{\langle g,g\rangle }}}$

Her köşede 1 değerini alan fonksiyon 1 olsun . O zaman özdeğeri 0 olan bir özfonksiyondur . ${\textstyle D^{\frac {1}{2}}1}$${\textstyle L^{\text{sym}}}$

Aslında, normalleştirilmiş simetrik Laplacian'ın özdeğerleri 0 = μ ₀ ≤ … ≤ μ _n−1 ≤ 2'yi sağlar. Bu özdeğerler (normalleştirilmiş Laplacian'ın spektrumu olarak bilinir), genel grafikler için diğer grafik değişmezleriyle iyi ilişkilidir.

Rastgele yürüyüş normalleştirilmiş Laplacian

Laplacian normalize rastgele yürüyüş olarak tanımlanır

${\displaystyle L^{\text{rw}}:=D^{-1}L}$

burada D derece matrisidir. Derece matris yana D çapraz ise, kendi ters sadece mukabil pozitif diyagonal girişlerin tanıma değerleri olan çapraz girişleri olan diyagonal matris olarak tanımlanır D . ${\textstyle D^{-1}}$

Yalıtılmış köşeler için (derece 0 olanlar), ortak bir seçim karşılık gelen elemanı 0'a ayarlamaktır . ${\textstyle L_{i,i}^{\text{rw}}}$

Bu kural, özdeğer 0'ın çokluğunun grafikteki bağlı bileşenlerin sayısına eşit olduğu güzel bir özellik ile sonuçlanır.

matris elemanları tarafından verilir ${\textstyle L^{\text{rw}}}$

${\displaystyle L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if}}\ i=j\ {\mbox{and}}\ \deg(v_ {i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_ {i}{\mbox{, }}v_{j}\\0&{\mbox{aksi halde}} ile bitişiktir.\end{cases}}}$

Rastgele yürüyüşle normalize edilmiş Laplacian'ın adı, bu matrisin olduğu gerçeğinden gelir , burada sadece bir rastgele yürüyenin grafikte geçiş matrisi bulunur. Örneğin, i'inci standart temel vektörü gösterelim . Ardından , köşe noktasından tek bir adım attıktan sonra rastgele yürüyenin konumlarının dağılımını temsil eden bir olasılık vektörü ; yani, . Daha genel olarak, vektör , grafiğin köşelerinde rastgele yürüyen birinin konumunun bir olasılık dağılımıysa, o zaman adımlardan sonra yürüyenin olasılık dağılımıdır . ${\textstyle L^{\text{rw}}=IP}$${\textstyle P=D^{-1}A}$${\textstyle e_{i}}$${\textstyle x=e_{i}P}$${\metin stili ben}$${\textstyle x_{j}=\mathbb {P} \left(v_{i}\to v_{j}\sağ)}$${\metin stili x}$${\textstyle x'=xP^{t}}$${\metin stili t}$

Bir kontrol edebilir

${\displaystyle L^{\text{rw}}=Kimlik^{-{\frac {1}{2}}}\left(IL^{\text{sym}}\right)D^{\frac {1 }{2}}}$,

yani bir benzeri normalize Laplace için . Bu nedenle genel olarak hermityen olmasa da gerçek özdeğerleri vardır. Gerçekten de, özdeğerleri (hermityen olan) ile uyumludur. ${\textstyle L^{\text{rw}}}$${\textstyle L^{\text{sym}}}$${\textstyle L^{\text{rw}}}$${\textstyle L^{\text{sym}}}$

Grafikler

Grafiklerde rastgele yürüyüşler hakkında bir kenara , basit bir yönsüz grafik düşünün . Yürütecin t − 1 zamanında j noktasında olduğu olasılık dağılımı göz önüne alındığında, yürütenin t zamanında i noktasında olma olasılığını düşünün (belirli bir tepe noktasına bağlı kenarlardan herhangi biri boyunca bir adım atma şansının tek tip olduğunu varsayarak) :

${\displaystyle p_{i}(t)=\sum _{j}{\frac {A_{ij}}{\deg \left(v_{j}\sağ)}}p_{j}(t-1) ,}$

veya matris-vektör notasyonunda:

${\displaystyle p(t)=AD^{-1}p(t-1).}$

( olarak ayarlanan denge, ile tanımlanır .) ${\textstyle t\sağ ok \infty }$${\textstyle p=AD^{-1}p}$

Bu ilişkiyi şu şekilde yeniden yazabiliriz:

${\displaystyle D^{-{\frac {1}{2}}}p(t)=\sol[D^{-{\frac {1}{2}}}AD^{-{\frac {1 }{2}}}\sağ]D^{-{\frac {1}{2}}}p(t-1).}$

${\textstyle A_{\text{indirgenmiş}}\equiv D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}}$indirgenmiş komşuluk matrisi adı verilen simetrik bir matristir . Dolayısıyla, bu rastgele yürüyüşte adım atmak , simetrik olduğu için basit bir işlem olan 'nin güçlerini almayı gerektirir . ${\textstyle A_{\text{azaltılmış}}}$${\textstyle A_{\text{azaltılmış}}}$

Ayrık Laplace operatörü olarak yorumlama

Laplace matrisi, ayrık Laplace operatörünün belirli bir durumunun matris temsili olarak yorumlanabilir . Böyle bir yorum, örneğin, Laplacian matrisini sonsuz sayıda köşesi ve kenarı olan ve sonsuz boyutta bir Laplacian matrisine yol açan grafikler durumuna genelleştirmeye izin verir.

Diyelim ki bir grafik boyunca ısı dağılımını tanımlayın , burada tepe noktasındaki ısı . Göre Newton'un soğutma yasası , ısı düğümden transfer düğüme orantılıdır düğümleri durumunda ve (birbirlerine bağlı değilse, ısı transfer edilir) bağlanır. Daha sonra ısı kapasitesi için , ${\metin stili \fi }$${\textstyle \phi _{i}}$${\metin stili ben}$${\metin stili ben}$${\metin stili j}$${\textstyle \phi _{i}-\phi _{j}}$${\metin stili ben}$${\metin stili j}$${\metin stili k}$

${\displaystyle {\begin{aligned}{\frac {d\phi _{i}}{dt}}&=-k\sum _{j}A_{ij}\left(\phi _{i}-\ phi _{j}\sağ)\\&=-k\left(\phi _{i}\sum _{j}A_{ij}-\sum _{j}A_{ij}\phi _{j} \sağ)\\&=-k\left(\phi _{i}\ \deg(v_{i})-\sum _{j}A_{ij}\phi _{j}\sağ)\\& =-k\sum _{j}\left(\delta _{ij}\ \deg(v_{i})-A_{ij}\sağ)\phi _{j}\\&=-k\sum _ {j}\sol(L_{ij}\sağ)\phi _{j}.\end{hizalı}}}$

Matris-vektör notasyonunda,

${\displaystyle {\begin{aligned}{\frac {d\phi }{dt}}&=-k(DA)\phi \\&=-kL\phi ,\end{hizalı}}}$

hangi verir

${\displaystyle {\frac {d\phi }{dt}}+kL\phi =0.}$

Bu denklemin, − L matrisinin Laplacian operatörünün yerini aldığı ısı denklemi ile aynı formu aldığına dikkat edin ; dolayısıyla, "grafik Laplacian". ${\textstyle \nabla ^{2}}$

Bu diferansiyel denkleme bir çözüm bulmak için, birinci dereceden matris diferansiyel denklemi çözmek için standart teknikleri uygulayın . Yani, yazma özvektörlerin lineer bir kombinasyonu olarak bir L (ki zamana bağlı katsayılı),${\metin stili \fi }$${\textstyle \mathbf {v} _{i}}$${\textstyle L\mathbf {v} _{i}=\lambda _{i}\mathbf {v} _{i}}$${\textstyle \phi (t)=\sum _{i}c_{i}(t)\mathbf {v} _{i}.}$

Orijinal ifadeye yerleştirme ( L simetrik bir matris olduğundan, birim norm özvektörleri diktir): ${\textstyle \mathbf {v} _{i}}$

${\displaystyle {\begin{aligned}0={}&{\frac {d\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\sağ)}{dt }}+kL\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\sağ)\\{}={}&\sum _{i}\left[{ \frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)L\mathbf {v} _{i}\sağ]\\{}= {}&\sum _{i}\left[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)\lambda _{i }\mathbf {v} _{i}\sağ]\\\Rightarrow 0={}&{\frac {dc_{i}(t)}{dt}}+k\lambda _{i}c_{i} (t),\\\end{hizalanmış}}}$

kimin çözümü

${\displaystyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}.}$

Daha önce gösterildiği gibi , L' nin özdeğerleri negatif değildir ve difüzyon denkleminin çözümünün bir dengeye yaklaştığını gösterir, çünkü sadece üstel olarak azalır veya sabit kalır. Bu aynı zamanda verilen ve başlangıç ​​koşulunun t'nin herhangi bir anında çözümün bulunabileceğini de gösterir. ${\textstyle \lambda _{i}}$${\textstyle \lambda _{i}}$${\textstyle c_{i}(0)}$

Her birini genel başlangıç ​​koşulu cinsinden bulmak için , birim norm özvektörlerine yansıtmanız yeterlidir ; ${\textstyle c_{i}(0)}$${\metin stili ben}$${\metin stili \fi (0)}$${\metin stili \fi (0)}$${\textstyle \mathbf {v} _{i}}$

${\displaystyle c_{i}(0)=\sol\langle \phi (0),\mathbf {v} _{i}\sağ\rangle}$.

Bu yaklaşım, yapılandırılmamış şebekelerde nicel ısı transferi modellemesine uygulanmıştır.

Yönlendirilmemiş grafikler söz konusu olduğunda, bu simetrik olduğundan ve spektral teoreme göre özvektörlerinin tümü ortogonal olduğundan işe yarar. Dolayısıyla, özvektörleri üzerine izdüşüm , başlangıç ​​koşulunun, üstel olarak ve birbirinden bağımsız olarak azalan bir dizi koordinata basit bir ortogonal koordinat dönüşümüdür. ${\metin stili L}$${\metin stili L}$

denge davranışı

Anlamak için , sadece terimler kalır nerede olanlardır beri, ${\textstyle \lim _{t\to \infty }\phi (t)}$${\textstyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}}$${\textstyle \lambda _{i}=0}$

${\displaystyle \lim _{t\to \infty}e^{-k\lambda _{i}t}={\begin{cases}0,&{\text{if}}&\lambda _{i} >0\\1,&{\text{if}}&\lambda _{i}=0\end{durumlar}}}$

Diğer bir deyişle, sistem denge durumu ile belirlemektedir çekirdek arasında . ${\metin stili L}$

Tanım olarak, tüm birlerin vektörü çekirdekte olduğundan. Grafikte ayrık bağlı bileşenler varsa , o zaman tüm birlerin bu vektörü, birler ve sıfırların bağımsız özvektörlerinin toplamına bölünebilir , burada her bağlı bileşen, bağlı bileşendeki öğelerde birler ve başka bir yerde sıfırlar ile bir özvektöre karşılık gelir. . ${\textstyle \sum _{j}L_{ij}=0}$${\textstyle \mathbf {v} ^{1}}$${\metin stili k}$${\metin stili k}$${\textstyle \lambda =0}$

Bunun sonucu, köşeleri olan bir grafiğin belirli bir başlangıç ​​koşulu için${\metin stili c(0)}$${\metin stili N}$

${\displaystyle \lim _{t\to \infty }\phi (t)=\left\langle c(0),\mathbf {v^{1}} \right\rangle \mathbf {v^{1}} }$

nerede

${\displaystyle \mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,\ldots ,1]}$

'nin her elemanı için , yani grafikteki her köşe için , şu şekilde yeniden yazılabilir: ${\textstyle \phi _{j}}$${\metin stili \fi }$${\metin stili j}$

${\displaystyle \lim _{t\to \infty }\phi _{j}(t)={\frac {1}{N}}\sum _{i=1}^{N}c_{i}( 0)}$.

Başka bir deyişle, kararlı durumda, grafiğin her bir köşesindeki aynı değere yakınsar, bu da tüm köşelerdeki başlangıç ​​değerlerinin ortalamasıdır. Bu, ısı difüzyon denkleminin çözümü olduğundan, sezgisel olarak mükemmel bir anlam ifade eder. Grafikteki komşu öğelerin, enerji birbirine bağlı tüm öğelere eşit olarak dağılıncaya kadar enerji alışverişi yapmasını bekliyoruz. ${\metin stili \fi }$

Bir ızgaradaki operatör örneği

Bu GIF, grafik laplacian tekniği ile çözüldüğü gibi difüzyonun ilerlemesini gösterir. Grafikteki her pikselin 8 komşu piksele bağlı olduğu bir ızgara üzerinde bir grafik oluşturulur. Görüntüdeki değerler daha sonra bu bağlantılar aracılığıyla zamanla komşularına düzgün bir şekilde yayılır. Bu özel görüntü, komşularına yavaşça yayılan üç güçlü nokta değeriyle başlar. Tüm sistem sonunda dengede aynı değere yerleşir.

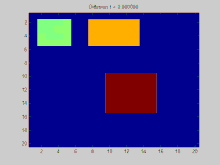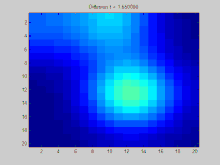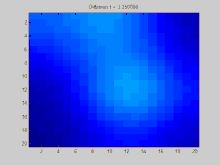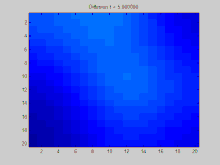
Bu bölüm, bir grafik aracılığıyla zaman içinde yayılan bir fonksiyon örneğini gösterir . Bu örnekteki grafik, ızgara üzerindeki noktaların sekiz komşusuna bağlı olduğu 2B ayrık bir ızgara üzerinde oluşturulmuştur. Üç başlangıç ​​noktasının pozitif bir değere sahip olduğu belirtilirken, ızgaradaki değerlerin geri kalanı sıfırdır. Zamanla, üstel azalma, bu noktalardaki değerleri tüm ızgara boyunca eşit olarak dağıtmak için hareket eder. ${\metin stili \fi }$

Bu animasyonu oluşturmak için kullanılan tam Matlab kaynak kodu aşağıda verilmiştir. Başlangıç ​​koşullarını belirleme, bu başlangıç ​​koşullarını Laplacian Matrisinin özdeğerlerine yansıtma ve bu öngörülen başlangıç ​​koşullarının üstel bozunmasını simüle etme sürecini gösterir.

N = 20; % The number of pixels along a dimension of the image
A = zeros(N, N); % The image
Adj = zeros(N * N, N * N); % The adjacency matrix

% Use 8 neighbors, and fill in the adjacency matrix
dx = [- 1, 0, 1, - 1, 1, - 1, 0, 1];
dy = [- 1, - 1, - 1, 0, 0, 1, 1, 1];
for x = 1:N
    for y = 1:N
        index = (x - 1) * N + y;
        for ne = 1:length(dx)
            newx = x + dx(ne);
            newy = y + dy(ne);
            if newx > 0 && newx <= N && newy > 0 && newy <= N
                index2 = (newx - 1) * N + newy;
                Adj(index, index2) = 1;
            end
        end
    end
end

% BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL EQUATION
Deg = diag(sum(Adj, 2)); % Compute the degree matrix
L = Deg - Adj; % Compute the laplacian matrix in terms of the degree and adjacency matrices
[V, D] = eig(L); % Compute the eigenvalues/vectors of the laplacian matrix
D = diag(D);

% Initial condition (place a few large positive values around and
% make everything else zero)
C0 = zeros(N, N);
C0(2:5, 2:5) = 5;
C0(10:15, 10:15) = 10;
C0(2:5, 8:13) = 7;
C0 = C0(:);

C0V = V'*C0; % Transform the initial condition into the coordinate system
% of the eigenvectors
for t = 0:0.05:5
    % Loop through times and decay each initial component
    Phi = C0V .* exp(- D * t); % Exponential decay for each component
    Phi = V * Phi; % Transform from eigenvector coordinate system to original coordinate system
    Phi = reshape(Phi, N, N);
    % Display the results and write to GIF file
    imagesc(Phi);
    caxis([0, 10]);
     title(sprintf('Diffusion t = %3f', t));
    frame = getframe(1);
    im = frame2im(frame);
    [imind, cm] = rgb2ind(im, 256);
    if t == 0
        imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1);
    else
        imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
    end
end

Negatif sürekli Laplacian'a yaklaşım

Laplacian matrisi grafiği ayrıca , sonlu farklar yöntemiyle elde edilen (pozitif yarı tanımlı) Laplacian operatörüne bir yaklaşımın matris biçimi olarak görüntülenebilir . (Bkz. Ayrık Poisson denklemi ) Bu yorumda, her grafik tepe noktası bir ızgara noktası olarak ele alınır; tepe noktasının yerel bağlanabilirliği , bu ızgara noktasında sonlu fark yaklaşımı şablonunu belirler, ızgara boyutu her zaman her kenar için birdir ve homojen Neumann sınır koşuluna karşılık gelen herhangi bir ızgara noktasında herhangi bir kısıtlama yoktur , yani , serbest sınır.

Yönlendirilmiş multigraflar

Yönlendirilmiş çoklu grafikler için Laplacian matrisinin bir analogu tanımlanabilir. Bu durumda Laplacian matrisi L şu şekilde tanımlanır:

${\görüntüleme stili L=DA}$

burada D ile diyagonal matris D _{I , I} tepe noktası outdegree için eşit i ve bir ile bir matris A _{i , j,} kenarlarda sayısına eşit i için j (döngüler de dahil).

Ayrıca bakınız

• rijitlik matrisi
• Direnç mesafesi
• Geçiş oranı matrisi
• Sonlu ağırlıklı grafikler üzerinde hesap
• Grafik Fourier dönüşümü

Referanslar

• T. Sunada, "Ayrık geometrik analiz", Proceedings of Symposia in Pure Mathematics, (ed. P. Exner, JP Keating, P. Kuchment, T. Sunada, A. Teplyaev), 77 (2008), 51–86.
• B. Bollobás , Modern Graph Theory , Springer-Verlag (1998, düzeltilmiş ed. 2013), ISBN  0-387-98488-7 , Chapters II.3 (Vektör Uzayları ve Grafiklerle İlişkili Matrisler), VIII.2 (The Bitişiklik Matrisi) ve Laplacian), IX.2 (Elektrik Ağları ve Rastgele Yürüyüşler).