Runge fenomeni - Runge's phenomenon

Runge işlevi (kırmızı, en yüksek merkezi tepe noktası); eşit aralıklı enterpolasyon noktaları (mavi, en düşük merkezi tepe noktası) ile 5. dereceden enterpolasyonlu polinom; ve eşit aralıklı enterpolasyon noktalarına sahip 9. dereceden enterpolasyon polinomu (yeşil, orta merkezi tepe)

Olarak matematiksel alanında sayısal analizi , Runge fenomeni ( Almanca: [ʁʊŋə] ) kullanılarak oluşan bir aralıkta kenarlarında salınım bir sorun polinom interpolasyon eşit aralıklı interpolasyon noktaları kümesi üzerinde yüksek derecede polinomlarla. Bu tarafından keşfedildi Carl David Tolmé Runge belirli işlevleri yaklaşmak için polinom interpolasyon kullanırken hatalar davranışını keşfetmek (1901). Keşif önemliydi çünkü daha yüksek derecelere gitmenin her zaman doğruluğu artırmadığını gösteriyor. Bu fenomen, Fourier serisi yaklaşımlarındaki Gibbs fenomenine benzer .

Tanıtım

Weierstrass teoremi her için bu durumları sürekli işlev f ( x , bir de tanımlanan) aralığı [ a , b ] bir dizi vardır polinom fonksiyonları p _{, n} ( x ) için , n = 0, 1, 2, ..., derece her en fazla n , [ a , b ] üzerinde tek biçimli yakınsama ile f ( x )'e yaklaşandır , çünkü n sonsuzluğa meyleder, yani,

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{a\leq x\leq b}\left|f(x)-P_{n}(x)\sağ|\sağ)= 0.}$

Bir arzularını durumu göz önüne alın sokmak yoluyla , n bir işlev +1 eşit aralıklı noktalar f ( x kullanılarak) n polinom -degree p _{, n} ( x , bu noktadan geçen). Doğal olarak, Weierstrass teoreminden daha fazla nokta kullanmanın f ( x ) 'in daha doğru bir yeniden yapılandırılmasına yol açacağı beklenebilir . Bununla birlikte, bu özel bir polinom fonksiyonların grubu p _{, n} ( x ) muntazam yakınsama özelliği garanti değildir; teorem, genel bir bulma yöntemi sağlamadan yalnızca bir dizi polinom fonksiyonunun var olduğunu belirtir .

P _{, n} ( x ) Bu şekilde üretilen olabilir uzak bilgi diverjans olarak f ( x gibi) , n artar; bu tipik olarak enterpolasyon noktalarının uçlarına yakın bir yerde büyüyen salınımlı bir modelde meydana gelir. Bu fenomen Runge'a atfedilir.

Sorun

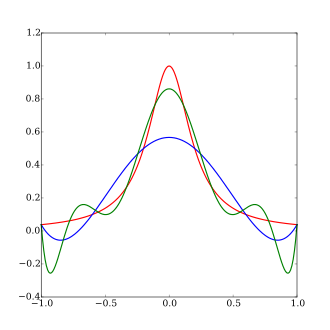
Runge işlevini düşünün

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}\,}$

( Agnesi Cadısı'nın ölçekli bir versiyonu ). Runge, bu fonksiyonun -1 ile 1 arasındaki x _i eşit uzaklık noktalarında enterpolasyonu yapıldığında şöyle olduğunu buldu:

${\displaystyle x_{i}={\frac {2i}{n}}-1,\quad i\in \sol\{0,1,\dots ,n\sağ\}}$

Derece ≤ n olan bir polinom P _n ( x ) ile  , elde edilen enterpolasyon aralığın sonuna doğru salınır, yani -1 ve 1'e yakındır. polinom artar:

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\sağ)=\infty . }$

Bu, eşit mesafedeki noktalarda yüksek dereceli polinom interpolasyonunun zahmetli olabileceğini göstermektedir.

Sebep

Runge fenomeni, bu problemin iki özelliğinin sonucudur.

• Büyüklüğü , n , bu özel işlev inci sırası türevlerinin hızlı büyür n artar.
• Noktalar arasındaki eşit mesafe , n arttığında hızla artan bir Lebesgue sabitine yol açar .

Bu fenomen grafiksel olarak açıktır, çünkü her iki özellik de salınımların büyüklüğünü artırmak için birleşir.

Üreten fonksiyon ile n mertebesindeki interpolasyon polinomu arasındaki hata şu şekilde verilir:

${\displaystyle f(x)-P_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0 }^{n}(x-x_{i})}$

bazıları için (-1, 1). Böylece, ${\görüntüleme stili \xi }$

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq \max _{-1\leq x\leq 1}{\frac {\ sol|f^{(n+1)}(x)\sağ|}{(n+1)!}}\max _{-1\leq x\leq 1}\prod _{i=0}^{ n}|x-x_{i}|}$.

Düğüm işleviyle belirtin${\ Displaystyle w_{n}(x)}$

${\displaystyle w_{n}(x)=(x-x_{0})(x-x_{1})\cdots (x-x_{n})}$

ve fonksiyonun büyüklüğünün maksimumu olsun : ${\ Displaystyle W_{n}}$${\ Displaystyle w_{n}}$

${\displaystyle W_{n}=\max _{-1\leq x\leq 1}|w_{n}(x)|}$.

Eşit mesafeli düğümlerle bunu kanıtlamak temeldir.

${\displaystyle W_{n}\leq n!h^{n+1}}$

adım boyutu nerede . ${\görüntüleme stili h=2/n}$

Ayrıca, ( n +1)-th türevinin sınırlı olduğunu varsayalım , yani ${\görüntüleme stili f}$

${\displaystyle \max _{-1\leq x\leq 1}|f^{(n+1)}(x)|\leq M_{n+1}}$.

Öyleyse,

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq M_{n+1}{\frac {h^{n+1}} {(n+1)}}}$.

Fakat Runge fonksiyonunun ( n +1)-th türevinin büyüklüğü n arttığında artar, çünkü . Sonuç olarak, ortaya çıkan üst sınır, , n sonsuza giderken sonsuza eğilim gösterir. ${\displaystyle M_{n+1}\leq (n+1)!5^{n+1}}$${\displaystyle (10/n)^{n+1}n!}$

Runge fenomenini açıklamak için sıklıkla kullanılsa da, hatanın üst sınırının sonsuza gitmesi gerçeği, elbette, hatanın kendisinin de n ile ıraksadığını ima etmez .

Soruna yönelik hafifletmeler

Enterpolasyon noktalarının değiştirilmesi

Salınım, özellikle, formül tarafından verilen asimptotik yoğunlukta ([-1,1] aralığında) aralığın kenarlarına doğru daha yoğun dağılmış düğümler kullanılarak en aza indirilebilir . Böyle bir düğüm kümesinin standart bir örneği , Runge işlevine yaklaşmadaki maksimum hatanın artan polinom sırası ile azalmasının garanti edildiği Chebyshev düğümleridir . Bu fenomen, yüksek dereceli polinomların genellikle eşit uzaklıkta düğümlerle enterpolasyon için uygun olmadığını göstermektedir. ${\displaystyle 1/{\sqrt {1-x^{2}}}}$

Yeniden örnekleme olmadan S-Runge algoritması

İyi davranmış düğüm kümeleri üzerinde yeniden örnekleme mümkün olmadığı için eşit mesafeli örnekler kullanılması gerektiğinde, S-Runge algoritması düşünülebilir. Bu yaklaşımda, orijinal düğüm kümesi, kararlı bir polinom yeniden yapılandırması sağlayarak Chebyshev düğümleri kümesi üzerinde eşlenir . Bu yöntemin özelliği, sahte düğümler olarak da adlandırılan eşlenen düğümlerde yeniden örneklemeye gerek olmamasıdır . Bu prosedürün bir Python uygulaması burada bulunabilir .

Parçalı polinomların kullanımı

Parçalı polinomlar olan spline eğrileri kullanılarak problemden kaçınılabilir . İnterpolasyon hatasını azaltmaya çalışırken, kullanılan polinomların derecesini arttırmak yerine spline'ı oluşturmak için kullanılan polinom parçalarının sayısı arttırılabilir.

Kısıtlı minimizasyon

Ayrıca daha yüksek dereceli bir polinom sığdırılabilir (örneğin, noktalar yerine mertebeden bir polinom kullanır ) ve birinci (veya ikinci) türevi minimum norma sahip olan enterpolasyonlu bir polinom sığdırabilir . ${\görüntüleme stili n}$${\displaystyle N=n^{2}}$${\ Displaystyle n+1}$${\ Displaystyle L^{2}}$

Benzer bir yaklaşım, polinomun türevi ile türevinin ortalama değeri arasındaki mesafenin kısıtlı bir versiyonunu en aza indirmektir . Açıkça, en aza indirmek için ${\görüntüleme stili L^{p}}$${\displaystyle m^{\mathrm {th} }}$${\displaystyle m^{\mathrm {th} }}$

${\displaystyle V_{p}=\int _{a}^{b}\left|{\frac {\operatöradı {d} ^{m}P_{N}(x)}{\operatöradı {d} x^ {m}}}-{\frac {1}{ba}}\int _{a}^{b}{\frac {\operatöradı {d} ^{m}P_{N}(z)}{\operatöradı {d} z^{m}}}\operatöradı {d} z\right|^{p}\operatöradı {d} x-\sum _{i=1}^{n}\lambda _{i}\, \left(P_{N}(x_{i})-f(x_{i})\sağ),}$

nerede ve , polinom katsayıları ve Lagrange çarpanları ile ilgili olarak , . olduğunda , Lagrange çarpanları tarafından üretilen kısıt denklemleri , tüm noktalardan geçen minimum polinoma indirgenir . Karşı uçta, parçalı bir polinom yaklaşımına çok benzeyen bir forma yaklaşacaktır. Zaman , özellikle, doğrusal parçalı polinomları yaklaşımlar, düz çizgiler ile interpolasyon noktalarını birleştiren yani. ${\ Displaystyle N\geq n-1}$${\görüntüleme stili m<N}$${\displaystyle \lambda _{i}}$${\görüntüleme stili N=n-1}$${\görüntüleme stili P_{N}(x)}$${\görüntüleme stili n}$${\displaystyle \lim _{N\rightarrow \infty }P_{N}(x)}$${\görüntüleme stili m=1}$${\displaystyle \lim _{N\rightarrow \infty }P_{N}(x)}$

Minimize etme sürecinde oynadığı rol , ortalama değerden uzaklaşan dalgalanmaların boyutunun önemini kontrol etmektir. Ne kadar büyükse , küçük dalgalanmalara kıyasla daha büyük dalgalanmalar o kadar cezalandırılır. Öklid normunun en büyük avantajı, analitik çözümlere izin vermesi ve yalnızca tek bir minimuma sahip olacağını garanti etmesidir. içinde birden fazla minimum olabileceği zaman , bulunan belirli bir minimumun yerel bir minimum yerine küresel minimum olmasını sağlamayı zorlaştırır . ${\görüntüleme stili p}$${\displaystyle V_{p}}$${\görüntüleme stili p}$${\görüntüleme stili p=2}$${\displaystyle V_{p}}$${\görüntüleme stili p\neq 2}$${\displaystyle V_{p}}$

En küçük kareler uydurma

Başka bir yöntem, en küçük kareler yöntemini kullanarak daha düşük dereceli bir polinom uydurmaktır . Genellikle, eşit mesafeli noktalar kullanılırken, eğer öyleyse en küçük kareler yaklaşımı iyi koşullandırılmıştır. ${\görüntüleme stili m}$${\displaystyle N<2{\sqrt {m}}}$${\görüntüleme stili P_{N}(x)}$

Bernstein polinomu

Bernstein polinomlarını kullanarak , bu yöntem hesaplama açısından oldukça pahalı olmasına rağmen, kapalı bir aralıktaki her sürekli fonksiyona düzgün bir şekilde yaklaşılabilir.

Harici Sahte Kısıtlamalar İnterpolasyonu

Bu yöntem, P"(x)'in enterpolasyon polinomunun ikinci türevi olduğu, enterpolasyon aralığının her iki tarafının uç noktalarına harici olarak yerleştirilmiş düğümler üzerinde P"(x)=0 tipi kısıtlamaların yoğun bir dağılımını optimal olarak istiflemeyi önerir. . Bu kısıtlamalar, enterpolasyon aralığına ait olmadıkları ve Runge işlevinin davranışıyla eşleşmedikleri için Harici Sahte Kısıtlamalar olarak adlandırılır. Yöntem, Runge Fenomeni'ni azaltmak için Parçalı polinomlardan (spline'lar) daha iyi bir enterpolasyon performansına sahip olduğunu göstermiştir.

Yaklaşım teorisinden ilgili ifadeler

Önceden tanımlanmış her enterpolasyon düğümü tablosu için, bu düğümlerdeki enterpolasyon polinomlarının dizisinin ayrıldığı sürekli bir fonksiyon vardır. Her sürekli fonksiyon için enterpolasyon sürecinin yakınsadığı bir düğüm tablosu vardır. Chebyshev enterpolasyonu (yani Chebyshev düğümlerinde ) her mutlak sürekli fonksiyon için düzgün bir şekilde yakınsar.

Ayrıca bakınız

• Sinüzoidal temel fonksiyonlar için Gibbs fenomeni ile karşılaştırın
• Taylor serisi
• Chebyshev düğümleri
• Schwarz feneri , yakınsama başarısızlığının bir başka örneği
• Stone-Weierstrass teoremi

Referanslar