Pappus'un altıgen teoremi - Pappus's hexagon theorem

Pappus'un altıgen teoremi: X , Y ve Z noktaları Pappus doğrusu üzerinde eşdoğrusaldır. Altıgen AbCaBc'dir .

Pappus teoremi: afin form
${\displaystyle Ab\paralel aB,Bc\paralel bC\Rightarrow Ac\paralel aC}$

Matematikte, Pappus'un altıgen teoremi ( İskenderiyeli Pappus'a atfedilir ) şunu belirtir:

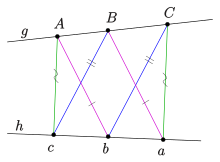
• Bir set verilen doğrudaş noktaları ve doğrudaş nokta başka bir dizi , o kesişim noktaları arasında hat çifti ve ve ve vardır doğrudaş yatan, Pappus hattı . Bu üç nokta, altıgenin "karşıt" kenarlarının kesişme noktalarıdır .${\görüntüleme stili A,B,C}$${\görüntüleme stili a,b,c}$${\görüntüleme stili X,Y,Z}$${\ Displaystyle Ab}$${\görüntüleme stili aB,Ac}$${\görüntüleme stili AC,Mc}$${\görüntüleme stili bC}$${\ Displaystyle AbCaBc}$

Bu tutan yansıtmalı düzlemde herhangi bir alan üzerinde, ancak herhangi bir nonkomutatif üzerinde yansıtmalı uçaklar için başarısız bölümü halka . "Teoremin" geçerli olduğu projektif düzlemlere pappian düzlemleri denir .

Projektif düzlem, Pappus çizgisi sonsuzdaki çizgi olacak şekilde kısıtlanırsa , ikinci diyagramda gösterilen Pappus teoreminin afin versiyonu elde edilir. ${\görüntüleme stili u}$

Pappus çizgisi ve çizgilerin ortak bir noktası varsa, Pappus teoreminin sözde küçük versiyonu elde edilir. ${\görüntüleme stili u}$${\görüntüleme stili g,h}$

Çift bu sıklığı teoremi bu belirli bir set bildiren eşzamanlı hatları ve eşzamanlı hatları başka bir dizi daha sonra, hat kesişme çiftlerinden elde edilen nokta çiftleri tarafından tayin edilen ve ve ve eşzamanlı vardır. ( Eşzamanlı , doğruların bir noktadan geçmesi anlamına gelir.) ${\görüntüleme stili A,B,C}$${\görüntüleme stili a,b,c}$${\görüntüleme stili x,y,z}$${\ Displaystyle A\ cap b}$${\ Displaystyle a\cap B,\;A\cap c}$${\displaystyle a\cap C,\;B\cap c}$${\displaystyle b\cap C}$

Pappus teoremi a, özel bir durum arasında Pascal teoremi bir konik için sınırlayıcı durumda olduğunda konik dejenere 2 düz çizgiler halinde. Pascal teoremi de Cayley-Bacharach teoreminin özel bir durumudur .

Pappus konfigürasyonu olan yapılandırma 9 hattı ve Puan 3 toplantı her hat ve her nokta toplantı 3 hat ile, pappus teoremi oluşur 9 puan. Genel olarak, pappus hattı kesişme noktası üzerinden geçmez ve . Bu yapılandırma kendinden çiftlidir . Özellikle, çizgiler ikili teoremin çizgilerinin özelliklerine sahip olduğundan ve of'nin eşdoğrusallığı ' nin eşzamanlılığına eşdeğer olduğundan , ikili teorem bu nedenle teoremin kendisiyle aynıdır. Levi grafik Pappus konfigürasyonunda Pappus grafiği , bir bipartit mesafe normal 18 köşe 27 kenarlı grafiktir. ${\görüntüleme stili ABC}$${\görüntüleme stili abc}$${\görüntüleme stili Bc,bC,XY}$${\görüntüleme stili x,y,z}$${\görüntüleme stili X,Y,Z}$${\görüntüleme stili Bc,bC,XY}$

Kanıt: afin formu

Pappus teoremi: kanıt

İfadenin afin formu kanıtlanabiliyorsa, o zaman Pappus teoreminin projektif formu kanıtlanır, çünkü bir pappian düzleminin bir projektif düzleme uzantısı benzersizdir.

Afin bir düzlemdeki paralellik nedeniyle, iki durum ayırt edilmelidir: ve . Basit bir ispatın anahtarı, "uygun" bir koordinat sistemi sunma olasılığıdır: ${\displaystyle g\değil \paralel h}$${\görüntüleme stili g\paralel h}$

Durum 1: çizgiler noktada kesişir . Bu durumda koordinatlar girilir, öyle ki (şemaya bakın). koordinatları var . ${\görüntüleme stili g,h}$${\displaystyle S=g\cap h}$
${\displaystyle \;S=(0,0),\;A=(0,1),\;c=(1,0)\;}$${\görüntüleme stili B,C}$${\displaystyle \;B=(0,\gamma ),\;C=(0,\delta ),\;\gamma ,\delta \notin \{0,1\}}$

Çizgilerin paralelliğin itibaren bir alır ve hatları paralelliğin verimleri . Dolayısıyla doğrunun eğimi vardır ve paralel doğrudur . ${\displaystyle Bc,\;Cb}$${\displaystyle b=({\tfrac {\delta }{\gamma }},0)}$${\görüntüleme stili Ab,Ba}$${\görüntüleme stili a=(\delta ,0)}$${\görüntüleme stili CA}$${\görüntüleme stili -1}$${\ Displaystyle Ac}$

Durum 2: (küçük teorem). Bu durumda koordinatlar şu şekilde seçilir . Paralellikten ve bir , sırasıyla ve alır ve en azından paralellik . ${\görüntüleme stili g\paralel h\ }$
${\displaystyle \;c=(0,0),\;b=(1,0),\;A=(0,1),\;B=(\gamma ,1),\;\gamma \neq 0}$${\displaystyle Ab\paralel Ba}$${\görüntüleme stili cB\paralel bC}$${\displaystyle \;C=(\gamma +1,1)\;}$${\displaystyle \;a=(\gamma +1,0)\;}$${\displaystyle \;Ac\paralel Ca\;}$

Homojen koordinatlarla ispat

İle homojen koordinatları seçin

${\displaystyle C=(1,0,0),\;c=(0,1,0),\;X=(0,0,1),\;A=(1,1,1)}$.

tarafından verilen satırlarda , olması gereken noktaları alın.${\görüntüleme stili AC,Ac,AX}$${\displaystyle x_{2}=x_{3},\;x_{1}=x_{3},\;x_{2}=x_{1}}$${\görüntüleme stili B,Y,b}$

${\displaystyle B=(p,1,1),\;Y=(1,q,1),\;b=(1,1,r)}$

bazıları için . Üç çizgi vardır , yani aynı noktadan ancak ve ancak geçerlerse geçerler . Üç satır koşulu ve denklemler ile aynı nokta geçmesine olup . Bu nedenle, diğer sekiz kümenin tümü çarpmanın değişmeli olmasından kaynaklanıyorsa, bu son üç satır kümesi eşzamanlıdır, yani . Eşdeğer olarak, doğrusaldır. ${\görüntüleme stili p,q,r}$${\görüntüleme stili XB,CY,cb}$${\displaystyle x_{1}=x_{2}p,\;x_{2}=x_{3}q,\;x_{3}=x_{1}r}$${\görüntüleme stili bir}$${\görüntüleme stili rqp=1}$${\görüntüleme stili Cb,cB}$${\görüntüleme stili XY}$${\displaystyle x_{2}=x_{1}q,\;x_{1}=x_{3}p,\;x_{3}=x_{2}r}$${\görüntüleme stili Z}$${\ Displaystyle rpq=1}$${\görüntüleme stili pq=qp}$${\görüntüleme stili X,Y,Z}$

Yukarıdaki kanıt ayrıca, Pappus teoreminin bir bölme halkası üzerinde bir yansıtmalı uzayı tutması için bölme halkasının bir (değişmeli) alan olmasının hem yeterli hem de gerekli olduğunu göstermektedir. Alman matematikçi Gerhard Hessenberg , Pappus teoreminin Desargues teoremini ima ettiğini kanıtladı . Genel olarak, Pappus'un teoremi bazı yansıtmalı düzlemler için geçerlidir, ancak ve ancak bu, değişmeli bir alan üzerinde bir yansıtmalı düzlem ise. Pappus teoreminin tutmadığı projektif düzlemler, değişmeli olmayan bölme halkaları üzerindeki Desargues projektif düzlemleri ve Desargues olmayan düzlemlerdir .

Doğrusal olması durumunda ispat geçersizdir . Bu durumda, örneğin farklı bir yansıtmalı referans kullanılarak alternatif bir kanıt sağlanabilir. ${\görüntüleme stili C,c,X}$

ikili teorem

Çünkü projektif düzlemler için ikiliği ilkesine Pappus ikili teoremi doğrudur:

6 satır ise iki ila dönüşümlü seçilir kalemler merkezleri ile , çizgiler ${\görüntüleme stili A,b,C,a,B,c}$${\görüntüleme stili G,H}$

${\displaystyle X:=(A\başlık b)(a\başlık B),}$

${\displaystyle Y:=(c\cap A)(C\cap a),}$

${\displaystyle Z:=(b\cap C)(B\cap c)}$

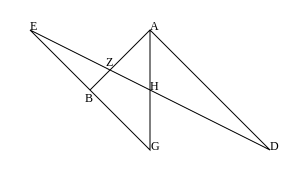
eşzamanlıdır, bu şu anlama gelir: ortak bir noktaları vardır. Soldaki diyagram yansıtmalı versiyonu, sağdaki ise noktaların sonsuzdaki noktalar olduğu afin versiyonu göstermektedir . Nokta doğru üzerindeyse, Pappus teoreminin "ikili küçük teoremi" elde edilir. ${\görüntüleme stili U}$
${\görüntüleme stili G,H}$${\görüntüleme stili U}$${\görüntüleme stili GH}$

• 

  ikili teorem: projektif form

• 

  ikili teorem: afin form

İkili "küçük teoremin" afin versiyonunda nokta da sonsuzda bir noktaysa , Thomsen teoremi , bir üçgenin kenarlarında 6 nokta üzerine bir ifade elde edilir (şemaya bakın). Thomsen figürü, aksiyomatik olarak tanımlanmış bir projektif düzlemi koordine etmede önemli bir rol oynar. Thomsen'in şeklinin kapanışının ispatı, yukarıda verilen "küçük teorem"in ispatı kapsamındadır. Ancak basit bir doğrudan kanıt da var: ${\görüntüleme stili U}$

Thomsen teoreminin ifadesi (şeklin kapanışı) yalnızca connect, kesişen ve paralel terimlerini kullandığından , ifade yakın bir şekilde değişmezdir ve şu şekilde koordinatlar verilebilir (sağdaki şemaya bakın). Akor dizisinin başlangıç ​​noktası , bir diyagramda verilen noktaların koordinatlarını kolayca doğrular, bu da şunu gösterir: son nokta ilk nokta ile çakışıyor. ${\displaystyle P=(0,0),\;Q=(1,0),\;R=(0,1)}$${\görüntüleme stili (0,\lambda ).}$

• 

  Thomsen figürü ( üçgenin noktaları ) Pappus'un küçük teoreminin ikili teoremi olarak ( sonsuzdadır!). ${\displaystyle \color {kırmızı}1,2,3,4,5,6}$${\görüntüleme stili PQR}$${\görüntüleme stili U}$

• 

  Thomsen rakamı: kanıt

Teoremin diğer ifadeleri

Üçgenler ve perspektifleri ve ' den ve dolayısıyla 'den de .${\görüntüleme stili XcC}$${\ Displaystyle BbY}$${\görüntüleme stili A}$${\görüntüleme stili bir}$${\görüntüleme stili Z}$

Pappus teoremi ve dualinin yukarıdaki tanımlamalarına ek olarak, aşağıdakiler eşdeğer ifadelerdir:

• Bir altıgenin altı köşesi dönüşümlü olarak iki doğru üzerinde bulunuyorsa, zıt kenar çiftlerinin kesiştiği üç nokta eşdoğrusaldır.
• Dokuz noktadan oluşan bir matriste düzenlenmiş (yukarıdaki şekilde ve açıklamada olduğu gibi) ve bir kalıcı olarak değerlendirildiği düşünülür , eğer ilk iki satır ve altı "köşegen" üçlü eşdoğrusal ise, o zaman üçüncü sıra eşdoğrusaldır.

${\displaystyle \left|{\begin{matrix}A&B&C\\a&b&c\\X&Y&Z\end{matrix}}\right|}$

Yani, eğer doğrularsa, Pappus'un teoremi bunun bir doğru olması gerektiğini belirtir . Ayrıca, aynı matris formülasyonunun, vb . eşzamanlı çizgilerin üçlüleri olduğunda teoremin ikili biçimi için geçerli olduğuna dikkat edin .${\displaystyle \ ABC,abc,AbZ,BcX,CaY,XbC,YcA,ZaB\ }$${\görüntüleme stili XYZ}$${\görüntüleme stili (A,B,C)}$

• İki farklı çizginin her biri üzerinde üç farklı nokta verildiğinde, çizgilerden biri üzerindeki her noktayı diğer çizgiden bir nokta ile eşleştirin, o zaman eşleşmeyen noktaların birleşimleri bir çizgi boyunca noktalarda (karşıt) çiftler halinde buluşacaktır.
• İki üçgen ise perspektif , en az iki farklı şekilde, o zaman üç şekilde perspektif vardır.
• Eğer ve eşzamanlıysa ve ve eşzamanlıysa, o zaman ve eşzamanlıdır.${\görüntüleme stili \;AB,CD,\;}$${\görüntüleme stili EF}$${\görüntüleme stili DE,FA,}$${\görüntüleme stili M.Ö.}$${\görüntüleme stili AD,BE,}$${\ Displaystyle CF}$

kökenler

Bilinen en eski haliyle, Pappus Teoremi, Pappus Koleksiyonu'nun VII. Kitabındaki Önermeler 138, 139, 141 ve 143'tür . Bu Önermelerde XII, XIII, XV ve ayırt VII üç kitabın ilk için lemmalarõn oluşan kısmen XVII olan Öklid 'in Porisms.

Lemmalar, bugün dört eşdoğrusal noktanın çapraz oranı olarak bilinen şey açısından kanıtlanmıştır. Daha önceki üç lemma kullanılır. Bunlardan ilki, Lemma III, aşağıdaki şemaya sahiptir (G'nin Γ, D'nin Δ, J'nin Θ ve L'nin Λ olduğu Pappus'un harflerini kullanır).

Burada, AB, AG ve AD olmak üzere üç eşzamanlı düz çizgi, J'de birleşen JB ve JE adlı iki doğru ile kesişmektedir. Ayrıca KL, AZ'ye paralel olarak çizilir. Sonra

KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB).

Bu oranlar bugün denklemler olarak yazılabilir:

KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB).

Son bileşik oran (yani JD : GD & BG : JB), bugün J, G, D ve B'nin aynı sıradaki doğrusal noktalarının çapraz oranı olarak bilinen şeydir ; bugün (J, G; D, B) ile gösterilir. Böylece bunun, A noktasında kesişen üç düz çizgiyi kesen belirli JD doğrusunun seçiminden bağımsız olduğunu gösterdik. Özellikle

(J, G; D, B) = (J, Z; H, E).

JE düz çizgisinin A'nın hangi tarafına düştüğü önemli değildir. Özellikle durum, Lemma X için diyagram olan bir sonraki diyagramdaki gibi olabilir.

Daha önce olduğu gibi (J, G; D, B) = (J, Z; H, E) var. Pappus bunu açıkça kanıtlamaz; ancak Lemma X bir tersidir, yani bu iki çapraz oran aynıysa ve BE ve DH düz çizgileri A'da kesişiyorsa, o zaman G, A ve Z noktaları eşdoğrusal olmalıdır.

Orijinal olarak gösterdiğimiz şey, (J, ∞; K, L) = (J, G; D, B) şeklinde yazılabilir, J, JK ve AG'nin (var olmayan) kesişiminin yerini alır. Pappus, aslında, diyagramı farklı harflere sahip olan Lemma XI'de bunu göstermektedir:

Pappus'un gösterdiği şey DE.ZH : EZ.HD :: GB : BE, bunu şöyle yazabiliriz.

(D, Z; E, H) = (∞, B; E, G).

Lemma XII için diyagram:

Lemma XIII için diyagram aynıdır, ancak genişletilmiş BA ve DG, N'de buluşurlar. Her durumda, G'den geçen düz çizgileri A'dan geçen üç düz çizgi tarafından kesilmiş olarak kabul ederek (ve çapraz oran denklemlerinin aşağıdakilerden sonra geçerli olduğunu kabul ederek) girişlerin permütasyonu),) elimizdeki Lemma III veya XI

(G, J; E, H) = (G, D; ∞ Z).

D'den geçen düz çizgileri, B'den geçen üç düz çizgiyle kesildiğini düşünürsek,

(L, D; E, K) = (G, D; ∞ Z).

Böylece (E, H; J, G) = (E, K; D, L), dolayısıyla Lemma X'e göre H, M ve K noktaları eşdoğrusaldır. Yani, ADEGBZ altıgenin karşılıklı kenar çiftlerinin kesişme noktaları eşdoğrusaldır.

Lemmas XV ve XVII, eğer M noktası HK ve BG'nin kesişimi olarak belirlenirse, o zaman A, M ve D noktaları eşdoğrusaldır. Yani, BEKHZG altıgenin karşılıklı kenar çiftlerinin kesişme noktaları eşdoğrusaldır.

Notlar

Referanslar

• Coxeter, Harold Scott MacDonald (1969), Geometriye Giriş (2. baskı), New York: John Wiley & Sons , ISBN 978-0-471-50458-0, MR  0123930
• Cronheim, A. (1953), "Hessenberg teoreminin kanıtı", Proceedings of the American Mathematical Society , 4 (2): 219–221, doi : 10.2307/2031794 , JSTOR  2031794
• Dembowski, Peter (1968), Sonlu Geometriler , Berlin: Springer Verlag
• Heath, Thomas (1981) [1921], Yunan Matematiğinin Tarihi , New York: Dover
• Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen , Berlin / Heidelberg: Springer, 61 (2): 161-172, doi : 10.1007/BF01457558 , ISSN  1432-1807
• Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt , Berlin
• Kline, Morris (1972), Antik Çağdan Modern Zamana Matematiksel Düşünce , New York: Oxford University Press
• Pambuccian, Victor; Schacht, Celia (2019), "Pappus ve Desargues teoremlerinin aksiyomatik kaderi", Dani, SG; Papadopoulos, A. (ed.), Tarihte Geometri , Springer, s. 355–399, ISBN 978-3-030-13611-6
• Hangisi, Zeytin (1971), Projektif Geometri , Rudolph Steiner Press, ISBN 0-85440-245-4

Dış bağlantılar

• Pappus en altıgen teoremi de kesme-düğüm
• Pappus en altıgen teoremine Çift at kesme-düğüm
• Pappus Teoremi: Dokuz ispat ve üç varyasyon