Mikrokanonik topluluk - Microcanonical ensemble

Olarak istatistiksel mekanik , mikrokanonik topluluğu a, istatistiksel grup toplam enerji tam olarak belirtilen bir mekanik sistem olası durumları gösterir. Sistemin, çevresiyle enerji veya parçacık alışverişinde bulunamaması anlamında yalıtılmış olduğu varsayılır, böylece ( enerjinin korunumu yoluyla ) sistemin enerjisi zamanla değişmez.

Mikrokanonik topluluğun birincil makroskopik değişkenleri, sistemdeki toplam parçacık sayısı (sembol: $N$ ), sistemin hacmi (sembol: $V$ ) ve sistemdeki toplam enerjidir (sembol: $E$ ). Bunların her birinin toplulukta sabit olduğu varsayılır. Bu nedenle, mikrokanonik topluluk bazen $NVE$ topluluğu olarak adlandırılır .

Basit bir ifadeyle, mikrokanonik topluluk, enerjisi $E$ merkezli bir aralık içinde kalan her mikro duruma eşit bir olasılık atanarak tanımlanır . Diğer tüm mikro durumlara sıfır olasılığı verilir. Olasılıkların toplamının 1 olması gerektiğinden, olasılık $P$ , enerji aralığındaki $W$ mikro durum sayısının tersidir ,

{\görüntüleme stili P=1/W,}

Enerji aralığı daha sonra , hala $E$ merkezli , sonsuz derecede dar olana kadar genişlikte azaltılır . Olarak sınırın , bu işlem, Mikrokanonik topluluk elde edilir.

uygulanabilirlik

Denge istatistiksel mekaniğinin temel varsayımları (özellikle a priori eşit olasılıklar varsayımı) ile bağlantısı nedeniyle , mikrokanonik topluluk teoride önemli bir kavramsal yapı taşıdır. Bazen denge istatistiksel mekaniğinin temel dağılımı olarak kabul edilir. Moleküler dinamik gibi bazı sayısal uygulamalarda da yararlıdır . Öte yandan, önemsiz olmayan sistemlerin çoğu, mikrokanonik toplulukta tanımlanması matematiksel olarak hantaldır ve ayrıca entropi ve sıcaklık tanımlarıyla ilgili belirsizlikler vardır. Bu nedenlerden dolayı, teorik hesaplamalar için genellikle diğer topluluklar tercih edilir.

Mikrokanonik topluluğun gerçek dünya sistemlerine uygulanabilirliği, sistem ve çevresi arasındaki etkileşimlerin yanı sıra sistemin hazırlanmasında kontrolsüz faktörlerden kaynaklanabilecek enerji dalgalanmalarının önemine bağlıdır. Genel olarak, bir sistem makroskopik olarak büyükse veya kesin olarak bilinen enerji ile üretiliyorsa ve daha sonra çevresinden neredeyse izole bir şekilde tutuluyorsa, dalgalanmalar ihmal edilebilir. Bu gibi durumlarda mikrokanonik topluluk uygulanabilir. Aksi takdirde, kanonik topluluk (dalgalanan enerji) veya büyük kanonik topluluk (dalgalanan enerji ve parçacık sayısı) gibi farklı topluluklar daha uygundur .

Özellikler

termodinamik büyüklükler

Mikrokanonik topluluğun temel termodinamik potansiyeli entropidir . En az üç olası tanımlar, faz ses işlevi açısından verilen her vardır $v (E)$ daha az enerji ile durumlarının toplam sayısını sayan, $E$ (bakınız kesin ifadeler matematiksel tanımı için bölüm $v$ ):

Boltzmann entropi
$S_{\text{B}}=k\log W=k\log \left(\omega {\frac {dv}{dE}}\sağ),$
'hacim entropisi'
$S_{v}=k\log v,$
'yüzey entropisi'
$S_{s}=k\log {\frac {dv}{dE}}=S_{\text{B}}-k\log \omega .$

Mikrokanonik toplulukta sıcaklık, harici bir kontrol parametresinden ziyade türetilmiş bir miktardır. Seçilen entropinin enerjiye göre türevi olarak tanımlanır. Örneğin, "sıcaklıklar" $T v$ ve $T s$ aşağıdaki gibi tanımlanabilir:

1/T_{v}=dS_{v}/dE,

1/T_{s}=dS_{s}/dE=dS_{\text{B}}/dE.

Entropi gibi, mikrokanonik topluluktaki sıcaklığı anlamanın birçok yolu vardır. Daha genel olarak, bu topluluğa dayalı tanımlar ve bunların termodinamik karşılıkları arasındaki uyum, özellikle sonlu sistemler için mükemmel değildir.

Mikrokanonik basınç ve kimyasal potansiyel şu şekilde verilir:

{\frac {p}{T}}={\frac {\kısmi S}{\kısmi V}};\qquad {\frac {\mu }{T}}=-{\frac {\kısmi S}{\kısmi N}}

Faz geçişleri

Katı tanımları altında, faz geçişleri , termodinamik potansiyel veya türevlerindeki analitik olmayan davranışa karşılık gelir . Bu tanımı kullanarak, mikrokanonik topluluktaki faz geçişleri, herhangi bir boyuttaki sistemlerde meydana gelebilir. Bu, faz geçişlerinin yalnızca termodinamik sınırda, yani sonsuz sayıda serbestlik derecesine sahip sistemlerde meydana gelebildiği kanonik ve büyük kanonik topluluklarla çelişir . Kabaca söylemek gerekirse, kanonik veya büyük kanonik toplulukları tanımlayan rezervuarlar, sonlu sistemlerin serbest enerjisindeki herhangi bir analitik olmayan davranışı "düzelten" dalgalanmalar getirir. Bu yumuşatma etkisi, serbest enerjinin analitik olmayan davranışa fazlasıyla iyi yaklaşabilmesi için yeterince büyük olan makroskopik sistemlerde genellikle ihmal edilebilir. Bununla birlikte, topluluklardaki teknik farklılık, küçük sistemlerin teorik analizinde önemli olabilir.

bilgi entropisi

Belirli bir mekanik sistem (sabit $N$ , $V$ ) ve belirli bir enerji aralığı için, olasılığın mikro durumlar üzerindeki düzgün dağılımı (mikrokanonik toplulukta olduğu gibi) topluluk ortalamasını $-⟨log P ⟩$ maksimize eder .

termodinamik analojiler

Ludwig Boltzmann'ın istatistiksel mekanikteki ilk çalışması, belirli bir toplam enerjiye sahip bir sistem için kendi adını taşıyan entropi denklemine yol açtı , $S = k log W$ , burada $W$ , sistem tarafından o enerjide erişilebilen farklı durumların sayısıdır. Boltzmann, ideal gazın özel durumunun yanı sıra, bir sistemin farklı durumları kümesini tam olarak neyin oluşturduğu konusunda çok derin bir ayrıntıya girmedi. Bu konu, keyfi mekanik sistemler için genelleştirilmiş istatistiksel mekaniği geliştiren ve bu makalede açıklanan mikrokanonik topluluğu tanımlayan Josiah Willard Gibbs tarafından sonuna kadar araştırıldı . Gibbs, mikrokanonik topluluk ve termodinamik arasındaki analojileri, özellikle birkaç serbestlik dereceli sistemler durumunda nasıl bozulduklarını dikkatle araştırdı. O bağlı olmayan mikrokanonik entropi iki başka şekilde belirlenmiş, $co$ - hacim ve yüzey entropi yukarıda tarif edilen. (Yüzey entropisinin Boltzmann entropisinden yalnızca $ω$ bağımlı bir kayma ile farklı olduğuna dikkat edin .)

Hacim entropisi $S v$ ve ilişkili $T v$ , termodinamik entropi ve sıcaklığa yakın bir analoji oluşturur. tam olarak bunu göstermek mümkün

dE=T_{\rm {v}}dS_{\rm {v}}-\langle P\rangle dV,

( $⟨ P ⟩$ topluluk ortalama basıncıdır) termodinamiğin birinci yasası için beklendiği gibi . Benzer bir denklem yüzeyi (Boltzmann) entropi ve ilişkili bulunabilir $T s$ ancak bu denklemde "basınç" Orta basınç ile ilgili olmayan karmaşık bir miktar.

Mikrokanonik $T v$ ve $T s$ sıcaklığına bunların benzer şekilde tamamen tatmin edici değildir. Termodinamik limitin dışında bir takım artefaktlar meydana gelir.

İki sistemi birleştirmenin önemsiz sonucu : Her biri bağımsız bir mikrokanonik topluluk tarafından tanımlanan iki sistem, termal temasa getirilebilir ve yine bir mikrokanonik topluluk tarafından açıklanan birleşik bir sistemde dengelenmesine izin verilebilir. Ne yazık ki, iki sistem arasındaki enerji akışı ilk göre tahmin edilemez $T$ 's. İlk $T'ler$ eşit olduğunda bile , aktarılan enerji olabilir. Ayrıca, kombinasyonun $T'si$ başlangıç değerlerinden farklıdır. Bu, sıcaklığın yoğun bir miktar olması gerektiği ve iki eşit sıcaklıktaki sistemin termal temasa getirilerek etkilenmemesi gerektiği sezgisiyle çelişir.
Birkaç parçacık sistemleri için garip davranış : Mikrokanonik Eşitlik teoremi gibi birçok sonuç , $T s$ cinsinden yazıldığında bir veya iki derecelik bir serbestlik kayması elde eder . Bu ofset küçük sistemler için önemlidir ve biz yapmak eğer öyleyse $S ler$ entropi analog, birkaç istisna serbestlik sadece bir veya iki derece ile sistemler için yapılması gerekmektedir.
Sahte negatif sıcaklıklar : Durumların yoğunluğu enerji ile azaldığında bir negatif $T s$ oluşur. Bazı sistemlerde durumların yoğunluğu enerjide monoton değildir ve bu nedenle $T s$ , enerji arttıkça birçok kez işaret değiştirebilir.

Bu sorunlara tercih edilen çözüm, mikrokanonik topluluğun kullanılmasından kaçınmaktır. Birçok gerçekçi durumda, bir sistem bir ısı banyosuna termostatlanır, böylece enerji tam olarak bilinmez. Daha sonra, daha doğru bir tanım , her ikisi de termodinamiğe tam karşılık gelen kanonik topluluk veya büyük kanonik topluluktur .

Topluluk için kesin ifadeler

Bir istatistiksel topluluğun kesin matematiksel ifadesi, söz konusu mekaniğin türüne (kuantum veya klasik) bağlıdır, çünkü bir "mikro durum" kavramı bu iki durumda oldukça farklıdır. Kuantum mekaniğinde köşegenleştirme , belirli enerjilere sahip ayrı bir dizi mikro durum sağlar . Klasik mekanik durum, bunun yerine kanonik faz uzayı üzerinde bir integral içerir ve faz uzayındaki mikro durumların boyutu biraz keyfi olarak seçilebilir.

Mikrokanonik topluluğu oluşturmak için, her iki mekanik türünde de önce bir enerji aralığı belirlemek gerekir. Aşağıdaki ifadelerde, fonksiyon ( $H'nin$ bir fonksiyonu , $E'de$ $ω$ genişliğinde tepe noktası), durumları içerecek enerji aralığını temsil etmek için kullanılacaktır. Bu işlevin bir örneği $f({\tfrac {HE}{\omega }})$

f(x)={\begin{cases}1,&\mathrm {if} ~|x|<{\tfrac {1}{2}},\\0,&\mathrm {aksi halde.} \ bitiş{durumlar}}

veya daha sorunsuz,

f(x)=e^{-\pi x^{2}}.

kuantum mekanik

Potansiyel bir kuyudaki bir parçacıktan oluşan bir kuantum sistemi için mikrokanonik topluluk örneği.

Bu sistemin tüm olası durumlarının grafiği. Mevcut durağan durumlar,

| ψ ben (x)| 2

.

Sadece dar bir enerji aralığındaki durumları içeren bir topluluk. Enerji genişliği sıfır alındığında, mikrokanonik bir topluluk elde edilir (aralığın en az bir durum içermesi şartıyla).

Parçacığın Hamiltoniyeni Schrödinger

tipidir

,

Ĥ

=

U

(

x

) +

p

2

/2

m

(potansiyel

U (x)

kırmızı bir eğri olarak çizilir). Her panel, çeşitli durağan durumlarla birlikte bir enerji konumu grafiğini ve durumların enerjideki dağılımını gösteren bir yan grafiği gösterir.

Kuantum mekaniğinde istatistiksel bir topluluk , ile gösterilen bir yoğunluk matrisi ile temsil edilir . Mikrokanonik topluluk , sistemin enerji özdurumları ve enerji özdeğerleri cinsinden bra–ket notasyonu kullanılarak yazılabilir . Enerji özdurumlarının eksiksiz bir temeli verildi $|$ $ψ$ $i$ $⟩$ , $i$ tarafından indekslenen mikrokanonik topluluk ${\ Displaystyle {\ şapka {\rho }}}$

{\hat {\rho }}={\frac {1}{W}}\sum _{i}f\left({\tfrac {H_{i}-E}{\omega }}\sağ )|\psi _{i}\rangle \langle \psi _{i}|,

burada $H i$ , tarafından belirlenen enerji özdeğerleridir (burada $Ĥ$ sistemin toplam enerji operatörüdür, yani Hamilton operatörü ). $W$ değeri , bunun normalleştirilmiş bir yoğunluk matrisi olması istenerek belirlenir ve böylece ${\hat {H}}|\psi _{i}\rangle =H_{i}|\psi _{i}\rangle$ ${\ Displaystyle {\ şapka {\rho }}}$

W=\sum _{i}f\sol({\tfrac {H_{i}-E}{\omega }}\sağ).

Durum hacmi fonksiyonu (entropiyi hesaplamak için kullanılır) ile verilir

v(E)=\sum _{H_{i}<E}1.

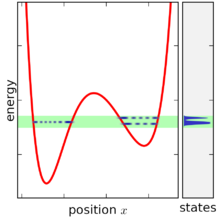
Mikrokanonik topluluk, enerji genişliği sıfıra giderken yoğunluk matrisinin limiti alınarak tanımlanır, ancak enerji genişliği enerji seviyeleri arasındaki boşluktan daha küçük olduğunda sorunlu bir durum ortaya çıkar. Çok küçük enerji genişliği için, $E'nin$ çoğu değeri için topluluk hiç mevcut değildir , çünkü aralık içinde hiçbir durum yoktur. Topluluk var olduğunda, tipik olarak yalnızca bir ( veya iki ) durum içerir, çünkü karmaşık bir sistemde enerji seviyeleri yalnızca tesadüfen eşittir ( bu nokta hakkında daha fazla tartışma için rasgele matris teorisine bakın ). Ayrıca, durum-hacim işlevi de yalnızca ayrık artışlarla artar ve bu nedenle türevi yalnızca sonsuz veya sıfırdır, bu da durumların yoğunluğunu tanımlamayı zorlaştırır. Bu problem, enerji aralığını tamamen sıfıra almayarak ve durum-hacim fonksiyonunu yumuşatarak çözülebilir, ancak bu, grubun tanımını daha karmaşık hale getirir, çünkü o zaman diğer değişkenlere (birlikte) ek olarak enerji aralığını belirtmek gerekli hale gelir. , bir $NVEω$ topluluğu).

klasik mekanik

Potansiyel bir kuyuda bir parçacıktan oluşan klasik bir sistem için mikrokanonik topluluk örneği.

Bu sistemin tüm olası durumlarının grafiği. Mevcut fiziksel durumlar, faz uzayında eşit olarak dağıtılır, ancak enerjide eşit olmayan bir dağılım vardır; yan grafik

dv / dE'yi

görüntüler .

Sadece dar bir enerji aralığındaki durumlarla sınırlı bir topluluk. Bu topluluk, faz uzayında ince bir kabuk olarak görünür. Enerji genişliği sıfır alındığında mikrokanonik bir topluluk elde edilir.

Her panel, faz uzayını (üstteki grafik) ve enerji-konum uzayını (alttaki grafik) gösterir. Parçacığın Hamiltoniyeni

H = U (x) + p 2 /2 m'dir

ve

U (x)

potansiyeli kırmızı bir eğri olarak gösterilir. Yan grafik, durumların enerjideki dağılımını gösterir.

Klasik mekanikte, bir topluluk, sistemin faz uzayı üzerinde tanımlanan bir birleşik olasılık yoğunluk fonksiyonu $ρ (p 1, \dots p n, q 1, \dots q n)$ ile temsil edilir . Faz alanı vardır $, n$ koordinatları genel olarak adlandırılan $q,$ $1$ $, ...$ $k$ $, n$ , ve $n,$ ilgili standart momentumları adı $p$ $1$ $, ...$ $s$ $, n$ .

Mikrokanonik topluluk için olasılık yoğunluk fonksiyonu:

\rho ={\frac {1}{h^{n}C}}{\frac {1}{W}}f({\tfrac {HE}{\omega }}),

nerede

$H$ sistemin toplam enerjisidir ( Hamiltonian ), fazın bir fonksiyonudur $(p 1, \dots q n)$ ,
$h$ birimleriyle keyfi ancak önceden tespit edilmiş sabit bir $enerji x zaman$ bir mikro durum kapsamını belirlemek ve doğru boyutları veren, $p'ye$ .
$C$ , genellikle aynı parçacıkların birbirleriyle yer değiştirebildiği parçacık sistemleri için kullanılan fazla sayım düzeltme faktörüdür.

Yine, $W$ değeri, $ρ'nın$ normalleştirilmiş bir olasılık yoğunluk fonksiyonu olması $istenerek$ belirlenir :

W=\int \ldots \int {\frac {1}{h^{n}C}}f({\tfrac {HE}{\omega }})\,dp_{1}\ldots dq_{ n}

Bu integral tüm faz uzayı üzerinden alınır . Durum hacmi işlevi (entropiyi hesaplamak için kullanılır) şu şekilde tanımlanır:

v(E)=\int \ldots \int _{H<E}{\frac {1}{h^{n}C}}\,dp_{1}\ldots dq_{n}.

Genişliği, enerji olarak $w$ sıfır alınır, değeri $W$ ile orantılı olarak azalır $co$ olarak $W = ω (dv / dE)$ .

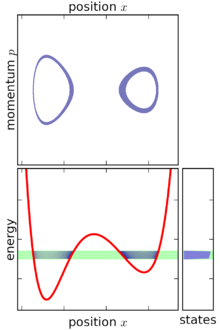
Yukarıdaki tanıma dayanarak, mikrokanonik topluluk, sabit enerjili bir yüzey üzerinde merkezlenmiş, faz uzayında sonsuz derecede ince bir kabuk olarak görselleştirilebilir. Mikrokanonik topluluk bu yüzeyle sınırlı olmasına rağmen, bu yüzey üzerinde mutlaka düzgün bir şekilde dağılmış değildir: faz uzayındaki enerji gradyanı değişirse, mikrokanonik topluluk yüzeyin bazı kısımlarında diğerlerinden daha "kalın" (daha konsantre) olur. . Bu özellik, mikrokanonik topluluğun kararlı durum topluluğu olmasını gerektirmenin kaçınılmaz bir sonucudur.

Örnekler

Ideal gaz

Mikrokanonik topluluktaki temel nicelik, verilen ile uyumlu faz uzayı hacmine eşittir . 'den tüm termodinamik büyüklükler hesaplanabilir. Bir için ideal bir gaz , enerji bu nedenle bir faktör katkıda parçacık pozisyonları, bağımsız için . Momenta, tersine, yarıçaplı bir -boyutlu (hiper) küresel kabukla sınırlıdır ; katkıları bu kabuğun yüzey hacmine eşittir. için elde edilen ifade şudur: ${\görüntüleme stili W(E,V,N)}$ ${\görüntüleme stili (E,V,N)}$ ${\görüntüleme stili W}$ ${\görüntüleme stili V^{N}}$ ${\görüntüleme stili W}$ ${\görüntüleme stili 3N}$ ${\sqrt {2mE}}$ ${\görüntüleme stili W}$

W={\frac {V^{N}}{N!}}{\frac {2\pi ^{3N/2}}{\Gamma (3N/2)}}\sol(2mE\sağ )^{(3N-1)/2}

burada bir gamma fonksiyonu ve faktör hesaba dahil edilmiş parçacıkların ayırt (bakınız Gibbs paradoksu ). Büyük olarak sınır Boltzmann entropi olan ${\görüntüleme stili \Gama (.)}$ ${\görüntüleme stili N!}$ ${\görüntüleme stili N}$ $S=k_{\mathrm {B} }\log W$

S=k_{\rm {B}}N\log \sol[{\frac {V}{N}}\sol({\frac {4\pi m}{3}}{\frac {E) }{N}}\sağ)^{3/2}\sağ]+{\frac {5}{2}}k_{\rm {B}}N+O\sol(\log N\sağ)

Bu aynı zamanda Sackur-Tetrode denklemi olarak da bilinir .

Sıcaklık tarafından verilir

{\frac {1}{T}}\equiv {\frac {\partial S}{\partial E}}={\frac {3}{2}}{\frac {Nk_{\mathrm {B } }}{E}}

bu da gazların kinetik teorisinin benzer sonucuyla uyumludur . Basıncın hesaplanması ideal gaz yasasını verir :

{\frac {p}{T}}\eşdeğer {\frac {\kısmi S}{\kısmi V}}={\frac {Nk_{\mathrm {B}}}{V}}\quad \ sağ ok \dört pV=Nk_{\mathrm {B} }T

Son olarak, kimyasal potansiyel olduğunu ${\görüntüleme stili \mu }$

\mu \equiv -T{\frac {\kısmi S}{\kısmi N}}=k_{\rm {B}}T\log \sol[{\frac {V}{N}}\, \sol({\frac {4\pi mE}{3N}}\sağ)^{3/2}\sağ]

Düzgün bir yerçekimi alanında ideal gaz

Mikrokanonik faz hacmi, düzgün bir yerçekimi alanında ideal bir gaz için açıkça hesaplanabilir .

Sonuçlar , z- yönünde sonsuz uzunlukta ve sabit bir kesit alanına sahip , termal olarak yalıtılmış bir kapta hapsedilmiş , her biri kütleye sahip , partiküllerden oluşan 3 boyutlu bir ideal gaz için aşağıda belirtilmiştir . Yerçekimi alanının kuvvetle eksi z yönünde hareket ettiği varsayılır . Fazı hacmi olan ${\görüntüleme stili N}$ ${\görüntüleme stili m}$ ${\görüntüleme stili A}$ ${\görüntüleme stili g}$ ${\görüntüleme stili W(E,N)}$

W(E,N)={\frac {(2\pi )^{3N/2}A^{N}m^{N/2}}{g^{N}\Gama (5N/2) )}}E^{{\frac {5N}{2}}-1}

toplam enerji nerede , kinetik artı yerçekimi. ${\görüntüleme stili E}$

Yüksekliğin bir fonksiyonu olarak gaz yoğunluğu , faz hacim koordinatları üzerinden integral alınarak elde edilebilir. Sonuç: ${\görüntüleme stili \rho (z)}$ ${\görüntüleme stili z}$

\rho (z)=\left({\frac {5N}{2}}-1\sağ){\frac {mg}{E}}\left(1-{\frac {mgz}{E) }}\sağ)^{{\frac {5N}{2}}-2}

Benzer şekilde, hız büyüklüğünün dağılımı (tüm yükseklikler üzerinden ortalaması alınır) $|{\vec {v}}|$

f(|{\vec {v}}|)={\frac {\Gama (5N/2)}{\Gama (3/2)\Gama (5N/2-3/2)}}\ kez {\frac {m^{3/2}|{\vec {v}}|^{2}}{2^{1/2}E^{3/2}}}\times \left(1- {\frac {m|{\vec {v}}|^{2}}{2E}}\sağ)^{\frac {5(N-1)}{2}}

Kanonik topluluktaki bu denklemlerin analogları , sırasıyla barometrik formül ve Maxwell-Boltzmann dağılımıdır . Limitinde , mikrokanonik ve kanonik ifadeler denk; ancak, sonlu için farklıdırlar . Özellikle mikrokanonik toplulukta konumlar ve hızlar istatistiksel olarak bağımsız değildir. Sonuç olarak, belirli bir hacimdeki ortalama kinetik enerji olarak tanımlanan kinetik sıcaklık, kap boyunca eşit değildir: $N\sağ ok \infty$ ${\görüntüleme stili N}$ ${\görüntüleme stili A\,dz}$

T_{\mathrm {kinetik} }={\frac {3E}{5N-2}}\left(1-{\frac {mgz}{E}}\sağ)

Buna karşılık, sıcaklık, herhangi bir . ${\görüntüleme stili N}$

Languages

In other projects