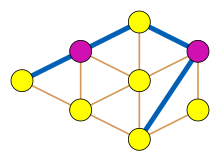
Pençesiz grafik - Claw-free graph

bir pençe

Bir matematik alanı olan grafik teorisinde , pençesiz bir grafik, indüklenmiş bir alt grafik olarak bir pençeye sahip olmayan bir grafiktir .

Bir pençe için başka bir isim olduğunu tam ikili grafik K 1,3 (olduğunu, bir yıldız grafiktir , üç kenardan üç yaprak ve bir merkezi tepe noktasına sahip). Pençesiz bir grafik, hiçbir indüklenmiş alt grafiğin bir pençe olmadığı bir grafiktir ; yani, dört köşenin herhangi bir alt kümesi, onları bu desende birbirine bağlayan sadece üç kenardan başkasına sahiptir. Aynı şekilde, bir pençe içermeyen grafik olan bir grafiktir mahalle herhangi bir tepe noktası olan tamamlayıcı a üçgen içermeyen grafik .

Pençesiz grafikler başlangıçta çizgi grafiklerin bir genellemesi olarak incelendi ve onlar hakkında üç önemli keşifle ek motivasyon kazandı: çift ​​sıralı tüm pençesiz bağlı grafiklerin mükemmel eşleşmelere sahip olması , maksimum bulmak için polinom zaman algoritmalarının keşfi pençesiz grafiklerde bağımsız kümeler ve pençesiz mükemmel grafiklerin karakterizasyonu . Yüzlerce matematiksel araştırma makalesinin ve çeşitli anketlerin konusudur.

Örnekler

Düzenli ikosahedron, köşeleri ve kenarları pençesiz bir grafik oluşturan bir polihedron.
  • Çizgi grafiğidir L ( G bir grafiğin) G pençe içermez; L ( G ) her bir kenar için bir tepe vardır G ve köşe bitişik olan L ( G karşılık gelen kenarları bir son nokta paylaşan zaman) , G . Bir çizgi grafiğidir L ( G üç kenarı çünkü eğer), bir kıskaç içeremez e 1 , e 2 ve e 3 de G bir kenarı tüm pay uç noktaları e 4 ile daha sonra pigeonhole prensip en az iki e 1 , E 2 , ve e 3 birbirleri ile olan son noktaların mutlaka bir pay bir. Çizgi grafikler, dokuz yasaklı alt grafik açısından karakterize edilebilir; pençe, bu dokuz grafiğin en basitidir. Bu karakterizasyon, pençesiz grafikleri incelemek için ilk motivasyonu sağladı.
  • De Bruijn grafikleri (ki köşeler temsil grafikleri N bitlik ikili dizileri bazı n ve kenarlar temsil eder ( n  - 1) bitlik bir çakışma iki sırası arasındaki) pençe içermez. Bunu göstermenin bir yolu, ( n  − 1)-bitlik diziler için de Bruijn grafiğinin çizgi grafiği olarak n -bitlik diziler için de Bruijn grafiğinin oluşturulmasıdır .
  • Tamamlayıcı herhangi bir üçgen içermeyen grafik pençe içermez. Bu grafikler özel bir durum olarak herhangi bir tam grafiği içerir .
  • Uygun aralık grafikleri , hiçbir aralığın başka bir aralık içermediği aralık ailelerinin kesişim grafikleri olarak oluşturulan aralık grafikleri , pençesizdir, çünkü dört düzgün kesişen aralık bir pençe deseninde kesişemez. Aynısı daha genel olarak uygun dairesel yay grafikleri için de geçerlidir .
  • Uçağın kromatik sayısı için bir alt sınır sağlamak için kullanılan yedi köşeli bir grafik olan Moser iş mili pençesizdir.
  • Birkaç grafikleri polihedrayı ve Politopunun grafiği de dahil olmak üzere, kıskaç içermez tetrahedron ve daha genel olarak herhangi bir simplex (tam bir grafik), grafikte oktahedron daha genel olarak ve çapraz politop ( izomorfik için kokteyl grafiği oluşturulmuştur tam bir grafikten mükemmel bir eşleşmeyi çıkararak), düzenli ikosahedron grafiği ve 16 hücreli grafiği .
  • SCHLAFLI grafiği , bir kuvvetle düzenli grafiği 27 köşeler ile, pençe-serbesttir.

Tanıma

n köşesi ve m kenarı olan belirli bir grafiğin O( n 4 ) zamanında pençesiz olduğunu doğrulamak, bir pençeyi indükleyip indüklemediklerini belirlemek için her 4 köşe kümesini test ederek kolaydır. Daha fazla verimlilik ve daha fazla karmaşıklıkla, grafiğin her köşesi için komşularının tamamlayıcı grafiğinin bir üçgen içermediğini kontrol ederek bir grafiğin pençesiz olup olmadığı test edilebilir . Bir grafik bir üçgen içeriyorsa ve yalnızca bir küp olarak bir bitişiklik matrisi yani üçgen bulgu olarak bağlanmış aynı asimptotik zamanda gerçekleştirilebilir, sıfır olmayan bir çapraz eleman içerir, n  x  n matris çarpımı . Bu nedenle, Coppersmith-Winograd algoritmasını kullanarak, bu pençesiz tanıma algoritması için toplam süre O( n 3.376 ) olacaktır.

Kloks, Kratsch & Müller (2000) , herhangi bir pençesiz grafikte, her bir köşenin en fazla 2 √ m komşusu olduğunu; aksi takdirde Turán teoremi ile köşenin komşuları üçgensiz bir grafiğin tümleyenini oluşturmak için yeterli kenarlara sahip olmayacaktı. Bu gözlem, yukarıda özetlenen hızlı matris çarpımına dayalı algoritmadaki her komşuluğun kontrolünün, 2 √ m  × 2 √ m matris çarpımı ile aynı asimptotik zaman sınırında veya daha da düşük dereceli köşeler için daha hızlı gerçekleştirilmesine izin verir. Bu algoritma için en kötü durum, Ω( √ m ) köşelerinin her birinin Ω( √ m ) komşusuna sahip olması ve kalan köşelerin birkaç komşuya sahip olması durumunda oluşur, bu nedenle toplam süresi O( m 3.376/2 ) = O( m 1.688 ) olur.

numaralandırma

Pençesiz grafikler üçgensiz grafiklerin tamamlayıcılarını içerdiğinden, n köşelerindeki pençesiz grafiklerin sayısı en az n'nin karesinde üssel olarak üçgensiz grafiklerin sayısı kadar hızlı büyür . Bağlı pençe içermeyen grafikler sayısı , n için düğüm, n  = 1, 2, ... olan

1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184.749, ... (dizi A022562 olarak OEIS ).

Grafiklerin bağlantısının kesilmesine izin verilirse, grafiklerin sayısı daha da fazladır:

1, 2, 4, 10, 26, 85, 302, 1285, 6170, ... (dizi A086991 olarak OEIS ).

Palmer, Read & Robinson'ın (2002) bir tekniği, grafik numaralandırma problemleri için alışılmadık şekilde, pençesiz kübik grafiklerin sayısının çok verimli bir şekilde sayılmasına izin verir .

Eşleşmeler

Sumner'ın çift sıralı pençesiz bağlı grafiklerin mükemmel eşleşmelere sahip olduğuna dair kanıtı: u'dan en uzak olan iki bitişik v ve w köşesinin kaldırılması, içinde aynı çıkarma işleminin tekrarlanabileceği bağlantılı bir alt grafik bırakır.

Sumner (1974) ve bağımsız olarak Las Vergnas (1975) , çift sayıda köşesi olan her pençesiz bağlı grafiğin mükemmel bir eşleşmeye sahip olduğunu kanıtladı . Diğer bir deyişle, grafikte her köşe tam olarak eşleşen kenarlardan birinin bitiş noktası olacak şekilde bir dizi kenar vardır. Çizgi grafikler için bu sonucun özel durumu, çift sayıda kenarı olan herhangi bir grafikte, kenarların iki uzunlukta yollara bölünebileceğini ima eder. Mükemmel eşleşmeler, tırnaksız grafiklerin başka bir karakterizasyonunu sağlamak için kullanılabilir: bunlar tam olarak, çift sıralı her bağlantılı indüklenmiş alt grafiğin mükemmel bir eşleşmeye sahip olduğu grafiklerdir.

Sumner'ın ispatı, daha güçlü bir şekilde, herhangi bir bağlantılı pençesiz grafikte, kaldırıldığında kalan grafiği bağlı bırakan bir çift bitişik köşe bulunabileceğini gösteriyor. Bunu göstermek için, Sumner köşe bir çift bulur u ve v grafik üzerinde birbirlerinden mümkün olduğunca uzak olan ve seçer ağırlık bir komşu olması v kadar ila u mümkün olduğu; onun gösterdiği gibi, ne v ne de w herhangi bir diğer düğümden u'ya giden en kısa yol üzerinde olamaz , bu nedenle v ve w'nin çıkarılması kalan grafiği bağlı bırakır. Eşleşen köşe çiftlerinin bu şekilde tekrar tekrar çıkarılması, verilen pençesiz grafikte mükemmel bir eşleşme oluşturur.

Aynı ispat fikri daha genel olarak, eğer u herhangi bir köşe ise, v , u'dan azami derecede uzak olan herhangi bir köşe ise ve w , v'nin u'dan azami derecede uzak olan herhangi bir komşusu ise, daha genel olarak geçerlidir . Ayrıca, grafikten v ve w'nin çıkarılması, u'ya olan diğer uzaklıkların hiçbirini değiştirmez . Bu nedenle, çift tespiti ile eşleşen bir oluşturma ve çıkarma işlemi VW maksimum uzak olan u tek ile gerçekleştirilebilir postorder kastetmek a enine arama kökü grafiğinin ağacı, u lineer zamanda. Chrobak, Naor & Novick (1989) , aynı problem için derinlik öncelikli aramaya dayalı alternatif bir doğrusal zaman algoritmasının yanı sıra verimli paralel algoritmalar sağlar.

Faudree, Flandrin ve Ryjáček (1997) aşağıdakiler dahil olmak üzere birkaç ilgili sonucu listeler: ( r  − 1)-bağlı K 1, çift ​​sıralı r- serbest grafikler herhangi bir r  ≥ 2 için mükemmel eşleşmelere sahiptir ; en fazla bir derece-bir tepe noktasına sahip tek sıralı pençesiz grafikler, tek bir döngü ve bir eşleşme olarak bölünebilir; herhangi k en herhangi biri bir pençe içermeyen grafik yarısı minimum derecede olan K veya köşelerin sayısı çift, grafik bir sahiptir k faktörünü; ve eğer tırnaksız bir grafik (2 k  + 1) bağlantılıysa, o zaman herhangi bir k- kenar eşleşmesi mükemmel bir eşleşmeye genişletilebilir.

Bağımsız kümeler

Maksimum olmayan bağımsız bir küme (iki menekşe düğümü) ve bir artırma yolu

Bir çizgi grafiğindeki bağımsız bir küme , altta yatan grafiğindeki bir eşleşmeye karşılık gelir, ikisi de bir bitiş noktasını paylaşmayan bir kenarlar kümesi. Çiçek algoritması arasında Edmonds (1965) , bir tespit maksimum eşleşen bir işlem eşdeğerdir polinom zaman içinde herhangi bir grafik, içinde en bağımsız set hattı grafiklerde. Bu, bağımsız olarak Sbihi (1980) ve Minty (1980) tarafından tüm pençesiz grafikler için bir algoritmaya genişletildi .

Her iki yaklaşım da, pençesiz grafiklerde, bağımsız bir kümede hiçbir tepe noktasının ikiden fazla komşusu olamayacağı ve bu nedenle iki bağımsız kümenin simetrik farkının en fazla iki dereceli bir alt grafiği indüklemesi gerektiği gözlemini kullanır ; yani, yolların ve döngülerin bir birleşimidir. Özellikle, I , bir non-maksimum bağımsız grubu olduğu, hatta döngü bir maksimum bağımsız kümesinden farklı ve sözde yolları artırmada : kaynaklı yolları değil uçları arasında dönüşümlü olarak I ve köşe I ve bunun için her iki bitiş noktası, sadece var I'de bir komşu . Herhangi bir artırma yolu ile I'in simetrik farkı daha büyük bir bağımsız küme verdiğinden, görev, maksimum eşleşmeleri bulmak için algoritmalarda olduğu gibi, daha fazlası bulunamayana kadar artan yolları aramaya indirgenir.

Sbihi'nin algoritması , Edmonds'un algoritmasının çiçek büzülme adımını yeniden yaratır ve benzer, ancak daha karmaşık bir klik büzülme adımı ekler . Minty'nin yaklaşımı, problem örneğini yardımcı bir çizgi grafiğine dönüştürmek ve artırma yollarını bulmak için doğrudan Edmonds'un algoritmasını kullanmaktır. Nakamura & Tamura 2001 tarafından yapılan bir düzeltmeden sonra , Minty'nin sonucu, polinom zamanında pençesiz grafiklerde bağımsız bir maksimum ağırlık kümesi bulma problemini çözmek için de kullanılabilir. Bu sonuçların daha geniş grafik sınıflarına genelleştirilmesi de bilinmektedir. Faenza, Oriolo & Stauffer (2011) , yeni bir yapı teoremi göstererek , ağırlıklı ortamda da çalışan bir kübik zaman algoritması verdi.

Boyama, klikler ve hakimiyet

Bir kusursuz bir grafik olan bir grafiktir renk sayısı ve büyüklüğü en fazla klik eşittir, ve burada her kaynaklı alt grafiği, bu eşitlik devam etmektedir. Şimdi, (bilinen güçlü mükemmel bir grafik teoremi mükemmel grafikleri neden Alt Graflar olarak bir tek döngüyü veya tek bir döngü tamamlayıcısını (sözde bir ya yok grafik olarak karakterize edilebilir olduğu) tek delik ). Bununla birlikte, uzun yıllar boyunca bu, yalnızca grafiklerin özel alt sınıfları için kanıtlanmış, çözülmemiş bir varsayım olarak kaldı. Bu alt sınıflardan biri pençesiz grafikler ailesiydi: birkaç yazar tarafından tek döngüleri ve tek delikleri olmayan pençesiz grafiklerin mükemmel olduğu keşfedildi. Mükemmel pençesiz grafikler polinom zamanında tanınabilir. Mükemmel bir pençesiz grafikte, herhangi bir tepe noktasının komşuluğu, iki parçalı bir grafiğin tamamlayıcısını oluşturur . Mümkündür renk mükemmel pençe içermeyen grafikler veya polinom zamanda, içlerinde maksimum klikler bulmak için.

Matematikte çözülmemiş problem :

Pençesiz grafikler her zaman kromatik numaralarına eşit liste kromatik numarasına sahip midir?

(matematikte daha fazla çözülmemiş problem)

Genel olarak, pençesiz bir grafikte en büyük kliği bulmak NP-zordur. Grafiğin optimal rengini bulmak da NP-zordur, çünkü (çizgi grafikler aracılığıyla) bu problem , bir grafiğin kromatik indeksini hesaplamanın NP-zor problemini genelleştirir . Aynı nedenle, 4/3'ten daha iyi bir yaklaşım oranı elde eden bir renk bulmak NP-zordur . Bununla birlikte, ikilik bir yaklaşıklık oranı, açgözlü bir renklendirme algoritması ile elde edilebilir , çünkü pençesiz bir grafiğin kromatik sayısı, maksimum derecesinin yarısından fazladır. Kenar listesi renklendirme varsayımının bir genellemesi, tırnaksız grafikler için liste kromatik numarasının kromatik sayıya eşit olduğunu belirtir ; bu iki sayı diğer grafik türlerinde birbirinden çok uzak olabilir.

Pençesiz grafikler χ -sınırlıdır , yani büyük kromatik sayıya sahip her pençesiz grafiğin büyük bir klik içerdiği anlamına gelir. Daha güçlü bir şekilde, Ramsey teoreminden , büyük maksimum dereceli her pençesiz grafiğin, derecenin kareköküyle kabaca orantılı büyüklükte büyük bir klik içerdiği sonucu çıkar. En az bir üç köşeli bağımsız küme içeren bağlantılı pençesiz grafikler için, kromatik sayı ile klik boyutu arasında daha güçlü bir ilişki mümkündür: bu grafiklerde, kromatik sayının en az yarısı büyüklüğünde bir klik vardır.

Her pençesiz grafik mükemmel olmasa da, pençesiz grafikler mükemmellikle ilgili başka bir özelliği de karşılar. Bir graf, bağımsız olan bir minimum baskın kümeye sahipse ve aynı özellik tüm indüklenmiş alt grafiklerinde geçerliyse, mükemmel hakimiyet olarak adlandırılır . Pençesiz grafikler bu özelliğe sahiptir. Bunu görmek için, pençesiz bir grafikte D'nin baskın bir küme olmasına izin verin ve v ve w'nin D' de iki bitişik köşe olduğunu varsayalım ; o zaman v'nin hakim olduğu, ancak w'nin hakim olmadığı köşeler kümesi bir klik olmalıdır (yoksa v bir pençenin merkezi olurdu). Bu klikteki her köşe D'nin en az bir başka üyesi tarafından domine ediliyorsa , o zaman v daha küçük bağımsız bir baskın küme üreterek çıkarılabilir ve aksi takdirde v , kliğindeki hakim olmayan köşelerden biri ile değiştirilebilir daha az komşuluk Bu değiştirme işlemini tekrarlayarak, sonunda D' den daha büyük olmayan baskın bir kümeye ulaşılır , bu nedenle özellikle başlangıç ​​kümesi D bir minimum baskın küme olduğunda bu işlem eşit derecede küçük bağımsız bir baskın küme oluşturur.

Bu hakimiyet mükemmellik özelliğine rağmen, pençesiz bir grafikte minimum hakim kümenin boyutunu belirlemek NP-zordur. Bununla birlikte, daha genel grafik sınıfları için durumun aksine, pençesiz bir grafikte minimum baskın kümeyi veya minimum bağlı baskın kümeyi bulmak sabit parametre izlenebilir : boyutta bir polinomla sınırlı zamanda çözülebilir baskın küme boyutunun üstel bir fonksiyonu ile çarpılan grafiğin değeri.

Yapı

Chudnovsky ve Seymour (2005) , Robertson ve Seymour tarafından kanıtlanmış minör-kapalı çizge aileleri için çizge yapı teoremine ve mükemmel grafikler için yapı teorisine benzer şekilde, pençesiz grafikler için bir yapı teorisi kanıtladıkları bir dizi makaleyi gözden geçirirler . Chudnovsky, Seymour ve ortak yazarlarının güçlü mükemmel grafik teoremini kanıtlamak için kullandıkları. Teori burada ayrıntılı olarak açıklanamayacak kadar karmaşıktır, ancak ona bir fikir vermek için iki sonucunun ana hatlarını vermek yeterlidir. İlk olarak, yarı-çizgi grafikleri (eşdeğer olarak, yerel eş-iki parçalı grafikler) olarak adlandırdıkları pençesiz grafiklerin özel bir alt sınıfı için , bu tür her grafiğin iki biçimden birine sahip olduğunu belirtirler:

  1. Bir bulanık dairesel aralık grafiği , uygun dairesel yay grafiklerini genelleştiren, bir daire üzerinde noktalar ve yaylarla geometrik olarak temsil edilen bir grafik sınıfı.
  2. Her bir kenarı bir bulanık doğrusal aralık grafiği ile değiştirerek bir çoklu grafikten oluşturulan bir grafik . Bu, çoklu grafiğin her kenarının bir köşe ile değiştirildiği bir çizgi grafiğinin yapısını genelleştirir. Bulanık doğrusal aralık grafikleri, bulanık dairesel aralık grafikleriyle aynı şekilde, ancak bir daire yerine bir çizgi üzerinde oluşturulur.

Chudnovsky ve Seymour, rastgele bağlantılı pençesiz grafikleri aşağıdakilerden birine sınıflandırır:

  1. Pençesiz grafiklerin altı özel alt sınıfı. Bunlardan üçü çizgi grafikler, uygun dairesel yay grafikleri ve bir ikosahedronun indüklenmiş alt grafikleridir; diğer üçü ek tanımlar içerir.
  2. Daha küçük pençesiz grafiklerden dört basit yolla oluşturulmuş grafikler.
  3. Antiprizmatik grafikler , her dört köşenin en az iki kenarlı bir alt grafiği indüklediği pençesiz grafikler olarak tanımlanan yoğun grafikler sınıfı .

Yapı teorisindeki çalışmaların çoğu, antiprizmatik grafiklerin daha fazla analizini içerir. SCHLAFLI grafiği , bir pençe içermeyen kuvvetle düzenli grafik parametreleri srg (27,16,10,8) ile analiz bu bölümünde önemli bir rol oynar. Bu yapı teorisi, çokyüzlü kombinatorikte yeni gelişmelere ve pençesiz grafiklerin kromatik sayısında yeni sınırların yanı sıra pençesiz grafiklerde baskın kümeler için yeni sabit parametreli izlenebilir algoritmalara yol açmıştır .

Notlar

Referanslar

Dış bağlantılar