Otonom sistem (matematik) - Autonomous system (mathematics)

Doğrusal otonom sistemin Poincaré haritalarını özelliklerine göre kararlı veya kararsız olarak sınıflandıran kararlılık diyagramı . Kararlılık genellikle diyagramın solunda artar. Bazı havuz, kaynak veya düğümler denge noktalarıdır . ${\ displaystyle x '= Balta,}$

2 boyutlu durum Faz düzlemini ifade eder .

In matematik , bir otonom sistem veya otonom diferansiyel denklem bir olduğunu sistem içinde sıradan diferansiyel denklemler açıkça bağlı değildir bağımsız değişken . Değişken zaman olduğunda, zamanla değişmeyen sistemler de denir .

Bağımsız değişkenin genellikle zaman olduğu varsayıldığı fizikteki birçok yasa, otonom sistemler olarak ifade edilir, çünkü şu anda geçerli olan doğa yasalarının geçmiş veya gelecekteki herhangi bir nokta için geçerli olanlarla aynı olduğu varsayılır .

Otonom sistemler, dinamik sistemlerle yakından ilişkilidir . Herhangi bir özerk sistem dinamik bir sisteme dönüştürülebilir ve çok zayıf varsayımlar kullanılarak dinamik bir sistem özerk bir sisteme dönüştürülebilir.

Tanım

Bir otonom sistem bir olan sıradan diferansiyel denklem sistemi formunun

${\ displaystyle {\ frac {d} {dt}} x (t) = f (x (t))}$

burada x , n -boyutlu Öklid uzayında değerler alır ; t genellikle zaman olarak yorumlanır.

Formun diferansiyel denklem sistemlerinden farklıdır

${\ displaystyle {\ frac {d} {dt}} x (t) = g (x (t), t)}$

hangi sistemin evrimini yöneten kanun yok değil sistemin mevcut durumu değil, aynı zamanda parametre üzerinde sadece bağlıdır t , yine sık sık zaman olarak yorumlanır; bu tür sistemler tanım gereği özerk değildir.

Özellikleri

Çözümler, yatay çevirilerde değişmez:

Otonom bir sistem için başlangıç ​​değer probleminin benzersiz bir çözümü olalım ${\ displaystyle x_ {1} (t)}$

${\ displaystyle {\ frac {d} {dt}} x (t) = f (x (t)) \ ,, \ quad x (0) = x_ {0}.}$

Sonra çözer ${\ displaystyle x_ {2} (t) = x_ {1} (t-t_ {0})}$

${\ displaystyle {\ frac {d} {dt}} x (t) = f (x (t)) \ ,, \ quad x (t_ {0}) = x_ {0}.}$

Gerçekten, sahip olduğumuzu ve dolayısıyla ${\ displaystyle s = t-t_ {0}}$${\ displaystyle x_ {1} (s) = x_ {2} (t)}$${\ displaystyle ds = dt}$

${\ displaystyle {\ frac {d} {dt}} x_ {2} (t) = {\ frac {d} {dt}} x_ {1} (t-t_ {0}) = {\ frac {d} {ds}} x_ {1} (s) = f (x_ {1} (s)) = f (x_ {2} (t)).}$

Başlangıç ​​koşulu için doğrulama önemsizdir,

${\ displaystyle x_ {2} (t_ {0}) = x_ {1} (t_ {0} -t_ {0}) = x_ {1} (0) = x_ {0}.}$

Misal

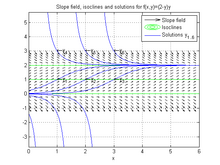
Denklem otonomdur, çünkü buna bağımsız değişken diyelim , denklemde açıkça görünmez. Bu denklem için eğim alanını ve izoklini çizmek için , GNU Octave / MATLAB'da aşağıdaki kod kullanılabilir. ${\ displaystyle y '= \ sol (2-y \ sağ) y}$${\ displaystyle x}$

Ffun = @(X, Y)(2 - Y) .* Y; % function f(x,y)=(2-y)y
[X, Y] = meshgrid(0:.2:6, -1:.2:3); % choose the plot sizes
DY = Ffun(X, Y); DX = ones(size(DY)); % generate the plot values
quiver(X, Y, DX, DY, 'k'); % plot the direction field in black
hold on;
contour(X, Y, DY, [0 1 2], 'g'); % add the isoclines(0 1 2) in green
title('Slope field and isoclines for f(x,y)=(2-y)y')

Grafikten fonksiyonun -değişmeyen olduğu ve çözümün şeklinin, yani herhangi bir kayma için olduğu gözlemlenebilir . ${\ displaystyle \ sol (2-y \ sağ) y}$${\ displaystyle x}$${\ displaystyle y (x) = y (x-x_ {0})}$${\ displaystyle x_ {0}}$

Denklemi MATLAB'da sembolik olarak çalıştırarak çözme

syms y(x);
equation = (diff(y) == (2 - y) * y);
% solve the equation for a general solution symbolically
y_general = dsolve(equation);

iki elde denge çözeltileri, ve , ve bilinmeyen bir sabit içeren bir üçüncü çözelti , . ${\ displaystyle y = 0}$${\ displaystyle y = 2}$${\ displaystyle C_ {3}}$-2 / (exp(C3 - 2 * x) - 1)

Başlangıç ​​koşulu için bazı spesifik değerler toplayarak, birkaç çözümün grafiğini ekleyebiliriz

İzoklinli eğim alanı ve çözümleri

% solve the initial value problem symbolically
% for different initial conditions
y1 = dsolve(equation, y(1) == 1); y2 = dsolve(equation, y(2) == 1);
y3 = dsolve(equation, y(3) == 1); y4 = dsolve(equation, y(1) == 3);
y5 = dsolve(equation, y(2) == 3); y6 = dsolve(equation, y(3) == 3);
% plot the solutions
ezplot(y1, [0 6]); ezplot(y2, [0 6]); ezplot(y3, [0 6]);
ezplot(y4, [0 6]); ezplot(y5, [0 6]); ezplot(y6, [0 6]);
title('Slope field, isoclines and solutions for f(x,y)=(2-y)y')
legend('Slope field', 'Isoclines', 'Solutions y_{1..6}');
text([1 2 3], [1 1 1], strcat('\leftarrow', {'y_1', 'y_2', 'y_3'}));
text([1 2 3], [3 3 3], strcat('\leftarrow', {'y_4', 'y_5', 'y_6'}));
grid on;

Nitel analiz

Otonom sistemler, faz uzayı kullanılarak nitel olarak analiz edilebilir ; tek değişkenli durumda, bu faz çizgisidir .

Çözüm teknikleri

Aşağıdaki teknikler tek boyutlu otonom diferansiyel denklemler için geçerlidir. Herhangi bir tek boyutlu mertebe denklemi, bir boyutlu birinci dereceden sisteme eşdeğerdir (birinci dereceden bir sisteme indirgemede açıklandığı gibi ), ancak bunun tersi zorunlu değildir. ${\ displaystyle n}$${\ displaystyle n}$

Birinci derece

Birinci dereceden otonom denklem

${\ displaystyle {\ frac {dx} {dt}} = f (x)}$

olan , ayrılabilir , bu nedenle kolayca entegre forma yeniden düzenleyerek çözülebilir

${\ displaystyle t + C = \ int {\ frac {dx} {f (x)}}}$

İkinci emir

İkinci dereceden otonom denklem

${\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} = f (x, x ')}$

daha zordur, ancak yeni değişkeni tanıtarak çözülebilir

${\ displaystyle v = {\ frac {dx} {dt}}}$

ve eksprese ikinci türevi arasında aracılığıyla zincir kuralı olarak ${\ displaystyle x}$

${\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} = {\ frac {dv} {dt}} = {\ frac {dx} {dt}} {\ frac {dv} {dx}} = v {\ frac {dv} {dx}}}$

böylece orijinal denklem olur

${\ displaystyle v {\ frac {dv} {dx}} = f (x, v)}$

bu bağımsız değişkene referans içermeyen birinci dereceden bir denklemdir . Çözme, bir işlevi olarak sağlar . Ardından, tanımını hatırlayarak : ${\ displaystyle t}$${\ displaystyle v}$${\ displaystyle x}$${\ displaystyle v}$

${\ displaystyle {\ frac {dx} {dt}} = v (x) \ quad \ Rightarrow \ quad t + C = \ int {\ frac {dx} {v (x)}}}$

bu örtük bir çözümdür.

Özel durum: x '' = f ( x )

Bağımsız olduğu özel durum ${\ displaystyle f}$${\ displaystyle x '}$

${\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} = f (x)}$

ayrı muameleden yararlanır. Bu tür denklemler klasik mekanikte çok yaygındır çünkü bunlar her zaman Hamilton sistemleridir .

Fikir kimliği kullanmaktır

${\ displaystyle {\ frac {dx} {dt}} = \ sol ({\ frac {dt} {dx}} \ sağ) ^ {- 1}}$

sıfıra bölmeden kaynaklanan herhangi bir sorunu engelleyen zincir kuralını takip eder .

Birinci dereceden otonom bir sistemin her iki tarafını ters çevirerek, aşağıdakiler açısından hemen entegre edilebilir : ${\ displaystyle x}$

${\ displaystyle {\ frac {dx} {dt}} = f (x) \ quad \ Rightarrow \ quad {\ frac {dt} {dx}} = {\ frac {1} {f (x)}} \ quad \ Rightarrow \ quad t + C = \ int {\ frac {dx} {f (x)}}}$

değişkenlerin ayrılması tekniğini görmenin başka bir yolu da budur. Daha yüksek mertebeden denklemlerle böyle bir şey yapabilir miyiz? Cevap, ikinci dereceden denklemler için evet, ancak yapılacak daha çok iş var. İkinci türev ile ilgili olarak bir türevi olarak ifade edilmelidir yerine : ${\ displaystyle x}$${\ displaystyle t}$

${\ displaystyle {\ begin {align} {\ frac {d ^ {2} x} {dt ^ {2}}} & = {\ frac {d} {dt}} \ left ({\ frac {dx} { dt}} \ right) = {\ frac {d} {dx}} \ left ({\ frac {dx} {dt}} \ right) {\ frac {dx} {dt}} \\ [4pt] & = {\ frac {d} {dx}} \ left (\ left ({\ frac {dt} {dx}} \ right) ^ {- 1} \ right) \ left ({\ frac {dt} {dx}} \ sağ) ^ {- 1} \\ [4pt] & = - \ left ({\ frac {dt} {dx}} \ right) ^ {- 2} {\ frac {d ^ {2} t} {dx ^ {2}}} \ left ({\ frac {dt} {dx}} \ sağ) ^ {- 1} = - \ left ({\ frac {dt} {dx}} \ sağ) ^ {- 3} {\ frac {d ^ {2} t} {dx ^ {2}}} \\ [4pt] & = {\ frac {d} {dx}} \ left ({\ frac {1} {2}} \ sol ({\ frac {dt} {dx}} \ sağ) ^ {- 2} \ sağ) \ uç {hizalı}}}$

Tekrar vurgulamak gerekirse: elde edilen şey, ikinci türevin bir türevi olarak ifade edilmesidir . Orijinal ikinci dereceden denklem artık entegre edilebilir: ${\ displaystyle t}$${\ displaystyle x}$

${\ displaystyle {\ begin {align} {\ frac {d ^ {2} x} {dt ^ {2}}} & = f (x) \\ {\ frac {d} {dx}} \ left ({ \ frac {1} {2}} \ left ({\ frac {dt} {dx}} \ right) ^ {- 2} \ right) & = f (x) \\\ left ({\ frac {dt} {dx}} \ sağ) ^ {- 2} & = 2 \ int f (x) dx + C_ {1} \\ {\ frac {dt} {dx}} & = \ pm {\ frac {1} { \ sqrt {2 \ int f (x) dx + C_ {1}}}} \\ t + C_ {2} & = \ pm \ int {\ frac {dx} {\ sqrt {2 \ int f (x) dx + C_ {1}}}} \ end {hizalı}}}$

Bu örtük bir çözümdür. En büyük potansiyel sorun, integrallerin basitleştirilememesidir; bu, entegrasyon sabitlerini değerlendirmede zorluk veya imkansızlık anlamına gelir.

Özel durum: x '' = x ' ⁿ f ( x )

Yukarıdaki yaklaşımı kullanarak, tekniği daha genel denkleme genişletebiliriz

${\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} = \ sol ({\ frac {dx} {dt}} \ sağ) ^ {n} f (x)}$

burada bazı parametreler ikiye eşit değildir. İkinci türev bir kuvvet içeren bir biçimde yazılabildiğinden, bu işe yarayacaktır . İkinci türevi yeniden yazmak, yeniden düzenlemek ve sol tarafı bir türev olarak ifade etmek: ${\ displaystyle n}$${\ displaystyle x '}$

${\ displaystyle {\ başla {hizalı} & - \ sol ({\ frac {dt} {dx}} \ sağ) ^ {- 3} {\ frac {d ^ {2} t} {dx ^ {2}} } = \ left ({\ frac {dt} {dx}} \ right) ^ {- n} f (x) \\ [4pt] & - \ left ({\ frac {dt} {dx}} \ sağ) ^ {n-3} {\ frac {d ^ {2} t} {dx ^ {2}}} = f (x) \\ [4pt] & {\ frac {d} {dx}} \ left ({ \ frac {1} {2-n}} \ left ({\ frac {dt} {dx}} \ right) ^ {n-2} \ right) = f (x) \\ [4pt] & \ left ( {\ frac {dt} {dx}} \ sağ) ^ {n-2} = (2-n) \ int f (x) dx + C_ {1} \\ [2pt] & t + C_ {2} = \ int \ left ((2-n) \ int f (x) dx + C_ {1} \ sağ) ^ {\ frac {1} {n-2}} dx \ end {hizalı}}}$

Sağ , çift ise +/− taşıyacaktır . Aşağıdaki durumlarda tedavi farklı olmalıdır : ${\ displaystyle n}$${\ displaystyle n = 2}$

${\ displaystyle {\ başla {hizalı} - \ sol ({\ frac {dt} {dx}} \ sağ) ^ {- 1} {\ frac {d ^ {2} t} {dx ^ {2}}} & = f (x) \\ - {\ frac {d} {dx}} \ left (\ ln \ left ({\ frac {dt} {dx}} \ sağ) \ sağ) & = f (x) \ \ {\ frac {dt} {dx}} & = C_ {1} e ^ {- \ int f (x) dx} \\ t + C_ {2} & = C_ {1} \ int e ^ {- \ int f (x) dx} dx \ end {hizalı}}}$

Daha yüksek siparişler

Üçüncü veya daha yüksek dereceden otonom denklemleri çözmek için benzer bir yöntem yoktur. Bu tür denklemler ancak, örneğin doğrusallık veya denklemin sağ tarafının yalnızca bağımlı değişkene bağımlılığı (yani türevleri değil) gibi başka bir basitleştirme özelliğine sahip oldukları takdirde tam olarak çözülebilirler . Üç boyutlu doğrusal olmayan otonom sistemlerin Lorenz çekicisi ve Rössler çekicisi gibi gerçekten kaotik davranışlar üretebileceği düşünüldüğünde, bu şaşırtıcı olmamalıdır .

Bu zihniyetle, ikinci mertebeden genel otonom olmayan denklemlerin açıkça çözülememesi çok da şaşırtıcı değildir, çünkü bunlar da kaotik olabilir (bunun bir örneği periyodik olarak zorlanan bir sarkaçtır).

Çok değişkenli durum

Şimdi elimizdeki nerede, bir olduğunu üzerinde boyutlu sütun vektör bağımlı . ${\ displaystyle \ mathbf {x} '(t) = A \ mathbf {x} (t)}$${\ displaystyle \ mathbf {x} (t)}$${\ displaystyle n}$${\ displaystyle t}$

Çözüm burada bir bir sabit vektörü. ${\ displaystyle \ mathbf {x} (t) = e ^ {At} \ mathbf {c}}$${\ displaystyle \ mathbf {c}}$${\ displaystyle n \ times 1}$

Ayrıca bakınız

• Zamanla değişmeyen sistem
• Otonom olmayan sistem (matematik)

Referanslar