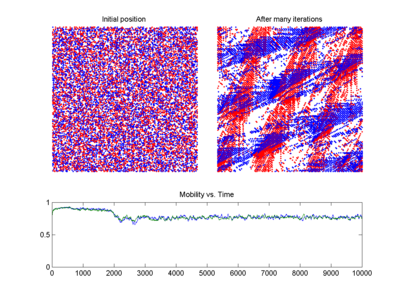
Kaos teorisi - Chaos theory

r = 28 , σ = 10 , b = 8/3 değerleri için Lorenz çekicisinin bir grafiği

Kaotik davranış gösteren bir ara enerjide çift ​​çubuklu sarkacın bir animasyonu . Sarkacı biraz farklı bir başlangıç ​​koşulundan başlatmak, çok farklı bir yörüngeyle sonuçlanacaktır . Çift çubuklu sarkaç, kaotik çözümlere sahip en basit dinamik sistemlerden biridir.

Kaos teorisi , kaos çalışmasına odaklanan disiplinler arası bir teori ve matematiğin dalıdır : görünüşte rastgele düzensizlik ve düzensizlik durumları, aslında başlangıç ​​koşullarına oldukça duyarlı olan temel kalıplar ve deterministik yasalar tarafından yönetilen dinamik sistemler . Kaos teorisi, kaotik karmaşık sistemlerin görünen rastgeleliği içinde , altta yatan kalıplar, birbirine bağlılık, sürekli geri besleme döngüleri , tekrarlama, kendi kendine benzerlik , fraktallar ve kendi kendine organizasyon olduğunu belirtir . Kelebek etkisi , kaos altında yatan ilke, bir bir halde küçük bir değişiklik açıklamaktadır deterministik doğrusal olmayan sistemi daha sonraki bir halde büyük farklılıklar (başlangıç koşullarına hassas bağımlılığı olduğu anlamına gelir) neden olabilir. Bu davranış için bir metafor içinde kanatlarını çırparak bir kelebek olduğunu Brezilya'da bir neden olabilir kasırga içinde Teksas .

Ölçümlerdeki hatalardan veya sayısal hesaplamadaki yuvarlama hatalarından kaynaklananlar gibi başlangıç ​​koşullarındaki küçük farklılıklar, bu tür dinamik sistemler için geniş ölçüde farklı sonuçlar verebilir ve genel olarak davranışlarının uzun vadeli tahminini imkansız hale getirebilir. Bu, bu sistemlerin deterministik olmasına , yani gelecekteki davranışlarının benzersiz bir evrim izlemesine ve hiçbir rastgele öğe içermeyen başlangıç ​​koşulları tarafından tamamen belirlenmesine rağmen gerçekleşebilir . Başka bir deyişle, bu sistemlerin deterministik doğası onları öngörülebilir kılmaz. Bu davranış, deterministik kaos veya basitçe kaos olarak bilinir . Teori Edward Lorenz tarafından şu şekilde özetlenmiştir :

Kaos: Şimdiki zaman geleceği belirlediğinde, ancak yaklaşık şimdiki zaman geleceği yaklaşık olarak belirlemediğinde.

Kaotik davranış, sıvı akışı, kalp atışı düzensizlikleri, hava ve iklim dahil olmak üzere birçok doğal sistemde mevcuttur. Borsa ve karayolu trafiği gibi yapay bileşenlere sahip bazı sistemlerde de kendiliğinden oluşur . Bu davranış, kaotik bir matematiksel modelin analizi yoluyla veya yineleme grafikleri ve Poincaré haritaları gibi analitik teknikler aracılığıyla incelenebilir . Kaos teorisi, meteoroloji , antropoloji , sosyoloji , çevre bilimi , bilgisayar bilimi , mühendislik , ekonomi , ekoloji , pandemik kriz yönetimi gibi çeşitli disiplinlerde uygulamalara sahiptir . Teori, karmaşık dinamik sistemler , kaos teorisinin kenarı ve kendi kendine bir araya gelme süreçleri gibi çalışma alanlarının temelini oluşturdu .

Tanıtım

Kaos teorisi, davranışları prensipte tahmin edilebilen deterministik sistemlerle ilgilidir. Kaotik sistemler bir süre için tahmin edilebilir ve sonra rastgele "görünür". Kaotik bir sistemin davranışının etkili bir şekilde tahmin edilebileceği süre üç şeye bağlıdır: tahminde ne kadar belirsizliğe tahammül edilebileceği, mevcut durumunun ne kadar doğru ölçülebileceği ve sistemin dinamiklerine bağlı bir zaman ölçeği. , Lyapunov zamanı denir . Lyapunov zamanlarının bazı örnekleri şunlardır: kaotik elektrik devreleri, yaklaşık 1 milisaniye; hava sistemleri, birkaç gün (kanıtlanmamış); iç güneş sistemi, 4 ila 5 milyon yıl. Kaotik sistemlerde, bir tahmindeki belirsizlik geçen zamanla katlanarak artar . Bu nedenle, matematiksel olarak, tahmin süresini ikiye katlamak, tahmindeki orantısal belirsizliğin karesini almaktan daha fazladır. Bu, pratikte, Lyapunov zamanının iki veya üç katından daha fazla bir aralıkta anlamlı bir tahmin yapılamayacağı anlamına gelir. Anlamlı tahminler yapılamadığında sistem rastgele görünür.

Kaos teorisi, tek veri ilişkileriyle açıklanamayan ve tahmin edilemeyen, ancak bütün, sürekli veri ilişkileriyle açıklanması ve tahmin edilmesi gereken dinamik sistemlerin davranışını araştırmak için nitel ve nicel bir analiz yöntemidir.

kaotik dinamikler

Harita tarafından tanımlanan X → 4 x (1 - x ) ve y → ( x + y) mod 1 başlangıç x pozisyonlarına görüntüler duyarlılık. Burada, iki dizi x ve y değeri, küçük bir başlangıç ​​farkından zaman içinde belirgin şekilde ayrılır.

Yaygın kullanımda "kaos", "düzensizlik durumu" anlamına gelir. Ancak, kaos teorisinde terim daha kesin olarak tanımlanır. Evrensel olarak kabul edilmiş bir matematiksel kaos tanımı olmamasına rağmen, orijinal olarak Robert L. Devaney tarafından formüle edilen yaygın olarak kullanılan bir tanım, dinamik bir sistemi kaotik olarak sınıflandırmak için şu özelliklere sahip olması gerektiğini söyler:

1. başlangıç ​​koşullarına duyarlı olmalıdır ,
2. topolojik olarak geçişli olmalıdır ,
3. yoğun periyodik yörüngelere sahip olmalıdır .

Bazı durumlarda, yukarıdaki son iki özelliğin aslında başlangıç ​​koşullarına duyarlılığı ifade ettiği gösterilmiştir. Kesikli zaman söz konusu olduğunda bu herkes için geçerlidir sürekli haritalar üzerinde metrik uzaylarda . Bu durumlarda, genellikle pratik olarak en önemli özellik olmasına rağmen, "başlangıç ​​koşullarına duyarlılık"ın tanımda belirtilmesine gerek yoktur.

Dikkat, aralıklarla sınırlıysa , ikinci özellik diğer ikisini ima eder. Alternatif ve genel olarak daha zayıf bir kaos tanımı, yukarıdaki listede yalnızca ilk iki özelliği kullanır.

Topolojik süpersimetrinin kendiliğinden bozulması olarak kaos

Sürekli zamanlı dinamik sistemlerde, kaos, tüm stokastik ve deterministik (kısmi) diferansiyel denklemlerin evrim operatörlerinin içsel bir özelliği olan topolojik süpersimetrinin kendiliğinden bozulması olgusudur. Bu dinamik kaos resmi, yalnızca deterministik modeller için değil, aynı zamanda fiziksel açıdan önemli bir genelleme olan dış gürültüye sahip modeller için de çalışır, çünkü gerçekte tüm dinamik sistemler, stokastik ortamlarından etkiyi deneyimler. Bu resimde, kaotik dinamiklerle ilişkili uzun menzilli dinamik davranış (örneğin kelebek etkisi ), Goldstone teoreminin bir sonucudur — kendiliğinden topolojik süpersimetri kırılmasına uygulamada.

Başlangıç ​​koşullarına duyarlılık

y değişkeni için grafikler oluşturmak için kullanılan Lorenz denklemleri. x ve z için başlangıç ​​koşulları aynı tutuldu ancak y için olanlar 1.001 , 1.0001 ve 1.00001 arasında değiştirildi . Değerleri , ve idi 45.92 , 16 ve 4 , sırasıyla. Grafikten de görülebileceği gibi, ilk değerlerdeki en ufak bir fark bile, üç durumda yaklaşık 12 saniyelik evrimden sonra önemli değişikliklere neden olur. Bu, başlangıç ​​koşullarına hassas bağımlılığın bir örneğidir.${\görüntüleme stili \rho }$${\görüntüleme stili \sigma }$${\görüntüleme stili \beta }$

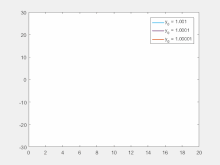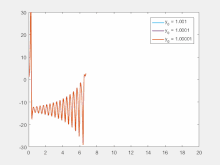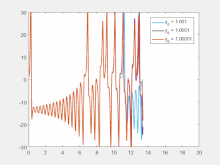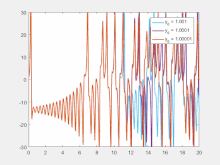
Başlangıç ​​koşullarına duyarlılık, kaotik bir sistemdeki her noktanın, önemli ölçüde farklı gelecekteki yolları veya yörüngeleri olan diğer noktalar tarafından keyfi olarak yakınlaştırıldığı anlamına gelir. Bu nedenle, mevcut yörüngede keyfi olarak küçük bir değişiklik veya bozulma, önemli ölçüde farklı gelecekteki davranışlara yol açabilir.

Başlangıç ​​koşullarına duyarlılık halk arasında " kelebek etkisi " olarak bilinir ve Edward Lorenz tarafından 1972'de Washington DC'deki American Association for the Advancement of Science'a verilen Öngörülebilirlik: Flap Yapar mı başlıklı bir makalenin başlığından dolayı bu adla bilinir. Bir Kelebeğin Kanatlarının Brezilya'daki görüntüsü Teksas'ta bir Tornado'yu mu tetikledi? . Çırpınan kanat, sistemin başlangıç ​​durumundaki küçük bir değişikliği temsil eder ve bu, büyük ölçekli olayların öngörülebilirliğini engelleyen bir olaylar zincirine neden olur. Kelebek kanatlarını çırpmamış olsaydı, genel sistemin yörüngesi çok farklı olabilirdi.

Başlangıç ​​koşullarına duyarlılığın bir sonucu, sistem hakkında sınırlı miktarda bilgi ile başlarsak (pratikte genellikle olduğu gibi), belirli bir sürenin ötesinde, sistemin artık tahmin edilebilir olmamasıdır. Bu, genellikle sadece bir hafta öncesinden tahmin edilebilen hava durumunda en yaygın olanıdır. Bu, gelecekteki olaylar hakkında herhangi bir şey söylenemeyeceği anlamına gelmez - sadece sistem üzerinde bazı kısıtlamaların mevcut olduğu. Örneğin, hava ile birlikte, sıcaklığın doğal olarak 100 °C'ye ulaşmayacağını veya (mevcut jeolojik çağda ) -130 °C'ye düşmeyeceğini biliyoruz, ancak bu, tam olarak hangi günün sıcaklığa sahip olacağını tahmin edebileceğimiz anlamına gelmez. yılın en sıcak sıcaklığı.

Daha matematiksel terimlerle, Lyapunov üssü , başlangıç ​​koşullarına duyarlılığı, bozulmuş başlangıç ​​koşullarından üstel sapma oranı biçiminde ölçer. Daha özel olarak ise, iki başlangıç verilen yörüngeleri de faz alanı , ilk ayırma ile, yakın sonsuz küçük olan , iki yörünge tarafından verilen bir oranda ıraksak sonunda ${\displaystyle \delta \mathbf {Z} _{0}}$

${\displaystyle |\delta \mathbf {Z} (t)|\yaklaşık e^{\lambda t}|\delta \mathbf {Z} _{0}|,}$

zaman nerede ve Lyapunov üssü. Ayırma hızı, ilk ayırma vektörünün oryantasyonuna bağlıdır, bu nedenle tüm bir Lyapunov üsleri spektrumu var olabilir. Lyapunov üslerinin sayısı, faz uzayının boyutlarının sayısına eşittir, ancak sadece en büyüğüne atıfta bulunmak yaygındır. Örneğin, maksimal Lyapunov üssü (MLE) en sık kullanılır, çünkü sistemin genel öngörülebilirliğini belirler. Pozitif bir MLE genellikle sistemin kaotik olduğunun bir göstergesi olarak alınır. ${\görüntüleme stili t}$${\ Displaystyle \ lambda }$

Yukarıdaki özelliğe ek olarak, başlangıç ​​koşullarının duyarlılığı ile ilgili başka özellikler de mevcuttur. Bunlar, örneğin ölçü-teorik karıştırmayı ( ergodik teoride tartışıldığı gibi ) ve bir K-sisteminin özelliklerini içerir .

periyodik olmayan

Kaotik bir sistem, gelişen değişken için, bu dizideki herhangi bir noktadan başlayarak periyodik davranış veren, kendilerini tam olarak tekrar eden değer dizilerine sahip olabilir. Bununla birlikte, bu tür periyodik diziler çekici olmaktan çok iticidir, yani gelişen değişken dizinin dışındaysa, ne kadar yakın olursa olsun, diziye girmeyecek ve aslında ondan ayrılacaktır. Bu nedenle, hemen hemen tüm başlangıç ​​koşulları için değişken, periyodik olmayan davranışla kaotik bir şekilde gelişir.

topolojik karıştırma

Lojistik haritadan bir dizi durumun altı yinelemesi geçti. İlk yineleme (mavi), esasen bir daire oluşturan başlangıç ​​koşuludur. Animasyon, dairesel başlangıç ​​koşullarının ilk ila altıncı yinelemesini gösterir. Yinelemelerde ilerledikçe karıştırmanın gerçekleştiği görülebilir . Altıncı yineleme, noktaların faz uzayında neredeyse tamamen dağıldığını gösterir. Yinelemelerde daha fazla ilerlemiş olsaydık, karıştırma homojen ve geri döndürülemez olurdu. Lojistik haritanın denklemi vardır . Lojistik haritanın durum uzayını iki boyuta genişletmek için ikinci bir durum , , if ve else olarak oluşturuldu .${\görüntüleme stili [x,y]}$${\displaystyle x_{k+1}=4x_{k}(1-x_{k})}$${\görüntüleme stili y}$${\displaystyle y_{k+1}=x_{k}+y_{k}}$${\displaystyle x_{k}+y_{k}<1}$${\displaystyle y_{k+1}=x_{k}+y_{k}-1}$

x → 4 x (1 – x ) ve y → ( x + y) mod 1 tarafından tanımlanan harita ayrıca topolojik karıştırmayı da gösterir . Burada mavi bölge dinamikler tarafından önce mor bölgeye, ardından pembe ve kırmızı bölgelere ve nihayetinde uzaya dağılmış dikey çizgilerden oluşan bir buluta dönüştürülür.

Topolojik karıştırma (veya topolojik geçişlilik zayıf durumu) araçlarının, böylece herhangi bir bölge ya da zaman içinde sistem geliştiği açık grubu barındırmayan faz alanı sonunda, bir başka bölge ile üst üste gelir. Bu matematiksel "karıştırma" kavramı, standart sezgiye karşılık gelir ve renkli boyaların veya sıvıların karıştırılması, kaotik bir sistemin bir örneğidir.

Topolojik karıştırma, kaosu yalnızca başlangıç ​​koşullarına duyarlılıkla eşitleyen popüler kaos açıklamalarından sıklıkla çıkarılır. Ancak başlangıç ​​koşullarına hassas bağımlılık tek başına kaos yaratmaz. Örneğin, bir başlangıç ​​değerini tekrar tekrar ikiye katlayarak üretilen basit dinamik sistemi düşünün. Bu sistem, her yerdeki başlangıç ​​koşullarına hassas bir bağımlılığa sahiptir, çünkü herhangi bir yakın nokta çifti sonunda geniş ölçüde ayrılır. Ancak, bu örnekte topolojik bir karışım yoktur ve bu nedenle kaos yoktur. Gerçekten de, son derece basit bir davranışı vardır: 0 dışındaki tüm noktalar, pozitif veya negatif sonsuzluğa eğilimlidir.

topolojik geçişlilik

Bir harita Boş olmayan herhangi çifti için eğer topolojik geçişli olduğu söylenir açık kümeler , vardır öyle ki . Topolojik geçişlilik, topolojik karıştırmanın daha zayıf bir versiyonudur . Bir harita topolojik geçişli ise Sezgisel olarak, daha sonra, bir nokta belirli bir x ve bir bölge V , bir nokta da mevcuttur y yakın x yörünge geçer V . Bu, sistemi iki açık kümeye ayırmanın imkansız olduğu anlamına gelir. ${\ Displaystyle f:X\to X}$ ${\görüntüleme stili U,V\alt küme X}$${\görüntüleme stili k>0}$${\displaystyle f^{k}(U)\cap V\neq \emptyset }$

İlgili önemli bir teorem Birkhoff Geçişlilik Teoremidir. Yoğun bir yörüngenin varlığının topolojik geçişliliği ima ettiğini görmek kolaydır. Birkhoff Geçişlilik Teoremi eğer belirten X'in bir olan ikinci sayılabilir , tam metrik uzay , sonra topolojik geçişlilik bir varlığını ima yoğun sette noktaların X yoğun yörüngelere sahiptir.

Periyodik yörüngelerin yoğunluğu

Kaotik bir sistemin yoğun periyodik yörüngelere sahip olması , uzaydaki her noktaya periyodik yörüngeler tarafından keyfi olarak yaklaşılması anlamına gelir. x → 4 x (1 – x ) ile tanımlanan tek boyutlu lojistik harita , periyodik yörünge yoğunluğuna sahip en basit sistemlerden biridir. Örneğin,  →  → (veya yaklaşık olarak 0.3454915 → 0.9045085 → 0.3454915) 2. periyodun (kararsız) bir yörüngesidir ve benzer yörüngeler 4., 8., 16. periyotlar için mevcuttur (aslında, Sharkovskii teoremi tarafından belirtilen tüm periyotlar için ) . ${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$${\displaystyle {\tfrac {5+{\sqrt {5}}}{8}}}$${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$

Sharkovskii'nin teoremi, Li ve Yorke'un (1975) düzenli bir periyot döngüsü sergileyen herhangi bir sürekli tek boyutlu sistemin, tamamen kaotik yörüngelerin yanı sıra her uzunluktaki düzenli döngüleri de göstereceğine dair kanıtının temelidir.

Garip çekiciler

Lorenz çeker kaotik davranış gösterir. Bu iki grafik, çekici tarafından işgal edilen faz uzayı bölgesindeki başlangıç ​​koşullarına hassas bağımlılığı gösterir.

x → 4 x (1 – x ) ile tanımlanan tek boyutlu lojistik harita gibi bazı dinamik sistemler her yerde kaotiktir, ancak çoğu durumda kaotik davranış sadece faz uzayının bir alt kümesinde bulunur. En çok ilgi çeken durumlar, kaotik davranış bir çekici üzerinde gerçekleştiğinde ortaya çıkar , o zamandan beri geniş bir başlangıç ​​koşulları kümesi, bu kaotik bölgeye yakınsayan yörüngelere yol açar.

Kaotik bir çekiciyi görselleştirmenin kolay bir yolu , çekicinin çekim havzasındaki bir nokta ile başlamak ve ardından basitçe sonraki yörüngesini çizmektir. Topolojik geçişlilik koşulu nedeniyle, bunun nihai çekicinin tamamının bir resmini üretmesi muhtemeldir ve aslında sağdaki şekilde gösterilen her iki yörünge de Lorenz çekicisinin genel şeklinin bir resmini verir. Bu çekici, Lorenz hava sisteminin basit bir üç boyutlu modelinden kaynaklanmaktadır . Lorenz çekicisi belki de en iyi bilinen kaotik sistem diyagramlarından biridir, çünkü muhtemelen sadece ilklerden biri değil, aynı zamanda en karmaşıklardan biridir ve bu nedenle çok ilginç bir modele yol açar. biraz hayal gücü, bir kelebeğin kanatlarına benziyor.

Sabit noktalı çekiciler ve limit çevrimlerinden farklı olarak, garip çekiciler olarak bilinen kaotik sistemlerden ortaya çıkan çekiciler , büyük ayrıntı ve karmaşıklığa sahiptir. Garip çekiciler hem sürekli dinamik sistemlerde (Lorenz sistemi gibi) hem de bazı ayrık sistemlerde ( Hénon haritası gibi ) meydana gelir. Diğer ayrık dinamik sistemler , sabit noktaların çekim havzaları arasındaki sınırda oluşan Julia kümesi adı verilen itici bir yapıya sahiptir. Julia setleri tuhaf kovucular olarak düşünülebilir. Hem garip çekiciler hem de Julia kümeleri tipik olarak fraktal bir yapıya sahiptir ve onlar için fraktal boyut hesaplanabilir.

Kaotik bir sistemin minimum karmaşıklığı

Dallanma diyagramı ve lojistik harita X → R x (- 1 x ). Her dikey dilim, belirli bir r değeri için çekiciyi gösterir . Diyagram , r arttıkça periyodun ikiye katlanmasını ve sonunda kaosa neden olduğunu gösterir.

Lojistik harita gibi ayrık kaotik sistemler, boyutları ne olursa olsun tuhaf çekiciler sergileyebilir . Parabolik maksimum ve birlikte tek boyutlu haritaların Evrenselliği Feigenbaum sabitleri , ayrık lazer dinamikleri için bir oyuncak modeli olarak önerilen harita ile de görülebilir: burada, elektrik alanı genliği açılımı, çatallanma parametre olarak lazer kazancıdır. Aralıktaki kademeli artış, dinamikleri düzenliden kaotik olana değiştirir ve lojistik harita için olanlarla niteliksel olarak aynı çatallanma şemasına sahiptir . ${\görüntüleme stili \delta =4.669201...}$${\görüntüleme stili \alfa =2.502907...}$${\displaystyle x\rightarrow Gx(1-\mathrm {tanh} (x))}$${\görüntüleme stili x}$${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili [0,\infty )}$

Buna karşılık, sürekli dinamik sistemler için, Poincaré–Bendixson teoremi , garip bir çekicinin yalnızca üç veya daha fazla boyutta ortaya çıkabileceğini gösterir. Sonlu boyutlu lineer sistemler asla kaotik değildir; dinamik bir sistemin kaotik davranış göstermesi için, ya doğrusal olmayan ya da sonsuz boyutlu olması gerekir .

Poincaré-Bendixson teoremi iki boyutlu diferansiyel denklem çok düzenli davranışa sahip olduğunu belirtmektedir. Aşağıda tartışılan Lorenz çekicisi, aşağıdaki gibi üç diferansiyel denklem sistemi tarafından üretilir :

${\displaystyle {\begin{hizalanmış}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma y-\sigma x,\\{\frac {\mathrm {d} y}{\mathrm {d} t}}&=\rho x-xz-y,\\{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z .\end{hizalanmış}}}$

nerede , ve makyaj sistem durumunu , zaman ve , , sistem olan parametreler . Sağ taraftaki terimlerin beşi doğrusal, ikisi ikinci derecedendir; toplam yedi terim. Bir başka iyi bilinen kaotik çekici, yedi terimden yalnızca bir tanesine sahip olan Rössler denklemleri tarafından üretilir . Sprott, belirli parametre değerleri için kaos sergileyen, yalnızca bir doğrusal olmayan terimi olan, yalnızca beş terimli üç boyutlu bir sistem buldu. Zhang ve Heidel, en azından tüketen ve muhafazakar ikinci dereceden sistemler için, sağ tarafta sadece üç veya dört terim bulunan üç boyutlu ikinci dereceden sistemlerin kaotik davranış sergileyemediğini gösterdi. Bunun nedeni, basitçe ifade etmek gerekirse, bu tür sistemlere yönelik çözümlerin iki boyutlu bir yüzeye asimptotik olması ve bu nedenle çözümlerin iyi davranmış olmasıdır. ${\görüntüleme stili x}$${\görüntüleme stili y}$${\görüntüleme stili z}$${\görüntüleme stili t}$${\görüntüleme stili \sigma }$${\görüntüleme stili \rho }$${\görüntüleme stili \beta }$

Poincaré–Bendixson teoremi, Öklid düzleminde sürekli bir dinamik sistemin kaotik olamayacağını gösterirken, Öklidyen olmayan geometriye sahip iki boyutlu sürekli sistemler kaotik davranış sergileyebilir. Belki şaşırtıcı bir şekilde, sonsuz boyutlu olmaları koşuluyla lineer sistemlerde de kaos meydana gelebilir. Fonksiyonel analiz olarak bilinen matematiksel analizin bir dalında bir lineer kaos teorisi geliştirilmektedir .

Sonsuz boyutlu haritalar

Bağlanmış ayrı haritaları basit genelleme dağınık haritalar arasındaki etkileşimi aracılık eder evrişim entegrali dayanmaktadır: , ${\displaystyle \psi _{n+1}({\vec {r}},t)=\int K({\vec {r}}-{\vec {r}}^{,},t)f [\psi _{n}({\vec {r}}^{,},t)]d{\vec {r}}^{,}}$

çekirdeğin ilgili bir fiziksel sistemin Yeşil işlevi olarak türetilen yayıcı olduğu yerde , lojistik harita veya karmaşık harita olabilir . Karmaşık harita örnekleri için Julia seti veya Ikeda haritası kullanılabilir. Mesafede dalga yayılımı sorunları zaman dalga boyu ile kabul edilmektedir çekirdek Yeşil fonksiyonunun bir forma sahip olabilir Schrödinger denklemi :. ${\displaystyle K({\vec {r}}-{\vec {r}}^{,},t)}$${\displaystyle f[\psi _{n}({\vec {r}},t)]}$${\displaystyle \psi \rightarrow G\psi [1-\tanh(\psi )]}$ ${\displaystyle f[\psi ]=\psi ^{2}}$ ${\displaystyle \psi _{n+1}=A+B\psi _{n}e^{i(|\psi _{n}|^{2}+C)}}$${\görüntüleme stili L=ct}$${\displaystyle \lambda =2\pi /k}$${\görüntüleme stili K}$

${\displaystyle K({\vec {r}}-{\vec {r}}^{,},L)={\frac {ik\exp[ikL]}{2\pi L}}\exp[{ \frac {ik|{\vec {r}}-{\vec {r}}^{,}|^{2}}{2L}}]}$.

pislik sistemleri

Olarak fizik , pislik üçüncü türevidir pozisyonda zamana göre. Bu nedenle, formun diferansiyel denklemleri

${\displaystyle J\sol({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\sağ)=0}$

bazen pislik denklemleri olarak adlandırılır . Üç birinci dereceden, adi, doğrusal olmayan diferansiyel denklem sistemine eşdeğer olan bir sarsıntı denkleminin, belirli bir anlamda kaotik davranış gösteren çözümler için minimum ayar olduğu gösterilmiştir. Bu, pislik sistemlerine matematiksel ilgiyi motive eder. Dördüncü veya daha yüksek türevi içeren sistemlere buna göre hiperjerk sistemleri denir.

Bir sarsıntı sisteminin davranışı bir sarsıntı denklemi ile tanımlanır ve bazı sarsıntı denklemleri için basit elektronik devreler çözümleri modelleyebilir. Bu devrelere sarsıntı devreleri denir.

Sarsıntı devrelerinin en ilginç özelliklerinden biri kaotik davranış olasılığıdır. Aslında, Lorenz çekicisi ve Rössler haritası gibi bazı iyi bilinen kaotik sistemler, geleneksel olarak, tek (oldukça karmaşık olsa da) bir sarsıntı denkleminde birleştirilebilen üç birinci mertebeden diferansiyel denklem sistemi olarak tanımlanır. Büyüklüğünde doğrusal olmayan bir sarsıntı denkleminin başka bir örneği : ${\görüntüleme stili x}$

${\displaystyle {\frac {\mathrm {d} ^{3}x}{\mathrm {d} t^{3}}}+A{\frac {\mathrm {d} ^{2}x}{\ matematik {d} t^{2}}}+{\frac {\mathrm {d} x}{\mathrm {d} t}}-|x|+1=0.}$

Burada A ayarlanabilir bir parametredir. Bu denklemin A =3/5 için kaotik bir çözümü vardır ve aşağıdaki sarsıntı devresi ile uygulanabilir; gerekli doğrusal olmama durumu iki diyot tarafından sağlanır:

Yukarıdaki devrede, hariç tüm dirençler eşit değerdedir ve tüm kapasitörler eşit boyuttadır. Baskın frekans ise . op amp 0'ın çıkışı x değişkenine, 1'in çıkışı x'in birinci türevine ve 2'nin çıkışı da ikinci türevine karşılık gelir. ${\ Displaystyle R_{A}=R/A=5R/3}$${\ Displaystyle 1/2\pi RC}$

Benzer devreler sadece bir diyot gerektirir veya hiç diyot gerektirmez.

Ayrıca, kaotik gerçek rasgele sayı üreteçleri için bir temel olan iyi bilinen Chua devresine bakın . Devrenin yapım kolaylığı, onu kaotik bir sistemin her yerde ve gerçek dünyadan bir örneği haline getirdi.

spontane düzen

Doğru koşullar altında, kaos kendiliğinden bir adım adım örüntüye dönüşür. Gelen Kuramoto modeli , dört koşullar kaotik bir sistemde senkronizasyon üretmek için yeterli olacaktır. Örnekleri arasında bağlanmış salınım arasında Christiaan Huygens 'sarkaç, ateş böceği, nöronlar , Londra Millennium köprü rezonans ve büyük dizileri Josephson eklemlerinin .

Tarih

Barnsley eğrelti otu , kaos oyunu kullanılarak yaratıldı . Doğal formlar (eğrelti otları, bulutlar, dağlar vb.) yinelenen bir işlev sistemi (IFS) aracılığıyla yeniden oluşturulabilir .

Kaos teorisinin erken savunucularından biri Henri Poincare idi . 1880'lerde, üç cisim problemini incelerken, periyodik olmayan, ancak sonsuza kadar artan veya sabit bir noktaya yaklaşmayan yörüngeler olabileceğini keşfetti. 1898'de Jacques Hadamard , " Hadamard'ın bilardosu " olarak adlandırılan, sabit negatif eğrilikli bir yüzey üzerinde sürtünmesiz kayan serbest bir parçacığın kaotik hareketinin etkili bir çalışmasını yayınladı . Hadamard, tüm yörüngelerin kararsız olduğunu, tüm parçacık yörüngelerinin pozitif bir Lyapunov üssü ile birbirinden katlanarak ayrıldığını gösterebildi .

Kaos teorisi, ergodik teori alanında başladı . Daha sonraki çalışmalarda, aynı zamanda doğrusal olmayan konusuyla ilgili diferansiyel denklemler tarafından gerçekleştirilmiştir George David Birkhoff , Andrey Nikolayeviç Kolmogorov , Mary Lucy Cartwright ve John Edensor Littlewood ve Stephen Smale . Smale dışında, bu çalışmaların hepsi doğrudan fizikten ilham aldı: Birkhoff örneğinde üç cisim problemi, Kolmogorov durumunda türbülans ve astronomik problemler ve Cartwright ve Littlewood durumunda radyo mühendisliği. Kaotik gezegensel hareket gözlemlenmemiş olsa da, deneyciler sıvı hareketinde türbülans ve radyo devrelerinde periyodik olmayan salınımla, gördüklerini açıklamak için bir teorinin yararı olmadan karşılaşmışlardı.

Yirminci yüzyılın ilk yarısındaki ilk kavrayışlara rağmen, kaos teorisi, ancak yüzyılın ortalarından sonra, bazı bilim adamlarına , o sırada hakim olan sistem teorisi olan lineer teorinin , gözlemlenenleri açıklayamadığı ilk kez açıkça ortaya çıktığında, resmiyet kazandı. lojistik haritanınki gibi belirli deneylerin davranışı . Belirsizliği ve basit " gürültüyü " ölçmek için atfedilen şey, kaos teorisyenleri tarafından incelenen sistemlerin tam bir bileşeni olarak kabul edildi.

Kaos teorisinin gelişiminin ana katalizörü elektronik bilgisayardı. Kaos teorisinin matematiğinin çoğu, elle yapılması pratik olmayan basit matematiksel formüllerin tekrar tekrar yinelenmesini içerir . Elektronik bilgisayarlar bu tekrarlanan hesaplamaları pratik hale getirirken, şekiller ve görüntüler bu sistemleri görselleştirmeyi mümkün kıldı. Chihiro Hayashi'nin Kyoto Üniversitesi'ndeki laboratuvarında yüksek lisans öğrencisi olan Yoshisuke Ueda, analog bilgisayarlarla deneyler yapıyordu ve 27 Kasım 1961'de "rastgele geçiş fenomeni" dediği şeyi fark etti. Yine de danışmanı o sırada vardığı sonuçlara katılmadı ve bulgularını 1970'e kadar rapor etmesine izin vermedi.

Türbülans içinde uç girdap bir gelen uçak kanadı. Bir sistemin türbülans yarattığı kritik noktanın çalışmaları, örneğin Landau-Hopf türbülans teorisini geliştiren Sovyet fizikçisi Lev Landau tarafından analiz edilen kaos teorisi için önemliydi . David Ruelle ve Floris Takens daha sonra Landau'ya karşı , kaos teorisinin ana kavramı olan garip bir çekici aracılığıyla akışkan türbülansının gelişebileceğini öngördü .

Edward Lorenz , teorinin ilk öncülerindendi. Kaosa olan ilgisi, 1961'de hava tahmini üzerine yaptığı çalışma sayesinde tesadüfen ortaya çıktı . Lorenz, hava simülasyonunu çalıştırmak için Royal McBee LGP-30 adlı basit bir dijital bilgisayar kullanıyordu . Tekrar bir veri dizisini görmek istedi ve zaman kazanmak için simülasyonu rotasının ortasında başlattı. Bunu, orijinal simülasyonun ortasındaki koşullara karşılık gelen verilerin bir çıktısını girerek yaptı. Şaşırtıcı bir şekilde, makinenin tahmin etmeye başladığı hava, önceki hesaplamadan tamamen farklıydı. Lorenz bunu bilgisayar çıktısına kadar takip etti. Bilgisayar 6 basamaklı hassasiyetle çalıştı, ancak çıktı değişkenleri 3 basamaklı bir sayıya yuvarladı, bu nedenle 0,506127 gibi bir değer 0,506 olarak yazdırıldı. Bu fark çok küçüktür ve o zamanki fikir birliği, bunun pratik bir etkisinin olmaması gerektiği yönündeydi. Ancak Lorenz, başlangıç ​​koşullarındaki küçük değişikliklerin uzun vadeli sonuçlarda büyük değişiklikler ürettiğini keşfetti. Lorenz çekicilerine adını veren Lorenz'in keşfi, ayrıntılı atmosferik modellemenin bile genel olarak kesin uzun vadeli hava tahminleri yapamayacağını gösterdi.

1963'te Benoit Mandelbrot , pamuk fiyatlarına ilişkin verilerde her ölçekte tekrar eden modeller buldu. Daha önce bilgi teorisi üzerinde çalışmış ve gürültünün bir Cantor kümesi gibi örüntülendiği sonucuna varmıştı : herhangi bir ölçekte gürültü içeren periyotların hatasız periyotlara oranı sabitti - bu nedenle hatalar kaçınılmazdı ve fazlalık dahil edilerek planlanmalıdır. Mandelbrot, hem "Nuh etkisi"ni (ani kesintili değişikliklerin meydana gelebileceği) hem de "Joseph etkisi"ni (bir değerin bir süre kalıcılığının meydana gelebileceği, ancak daha sonra aniden değişebileceği) tanımladı. Bu, fiyattaki değişikliklerin normal olarak dağıldığı fikrine meydan okudu . 1967'de, bir kıyı şeridinin uzunluğunun ölçüm aletinin ölçeğine göre değiştiğini, her ölçekte kendisine benzediğini ve sonsuz uzunlukta olduğunu gösteren " İngiltere'nin kıyısı ne kadardır? İstatistiksel özbenzerlik ve kesirli boyut " adlı kitabını yayınladı. sonsuz derecede küçük ölçüm cihazı. Bir sicim yumağının uzaktan bakıldığında bir nokta (0-boyutlu), oldukça yakından bakıldığında bir top (3-boyutlu) ya da kavisli bir iplik (1-boyutlu) olarak göründüğünü savunarak, bir nesne gözlemciye göredir ve kesirli olabilir. Olan düzensizlik farklı ölçeklerde üzerinde sabittir ( "kendi kendine benzerlik") a, bir amacı, fraktal (bunların örneklerine, Menger sünger , Sierpinski conta ve Koch eğrisi ya da kar tanesi uzun ancak sonsuz olduğu, belli bir alan çevreleyen ve bir sahiptir fraktal boyut circa 1,2619 arasında). 1982'de Mandelbrot , bir kaos teorisi klasiği haline gelen Doğanın Fraktal Geometrisini yayınladı . Dolaşım ve bronş sistemlerinin dallanması gibi biyolojik sistemlerin fraktal bir modele uyduğu kanıtlandı.

Aralık 1977'de, New York Bilimler Akademisi, David Ruelle, Robert May , James A. Yorke (matematikte kullanılan "kaos" teriminin yaratıcısı), Robert Shaw ve meteorolog Edward'ın katıldığı ilk kaos sempozyumunu düzenledi. Lorenz. Ertesi yıl Pierre Coullet ve Charles Tresser "Itérations d'endomorphismes et groupe de renormalisation"ı yayınladılar ve Mitchell Feigenbaum'un "Quantitative Universality for a Class of Nonlinear Transformations" adlı makalesi 3 yıllık hakem reddinden sonra nihayet bir dergide yayınlandı. Böylece Feigenbaum (1975) ve Coullet & Tresser (1978) , kaos teorisinin birçok farklı fenomene uygulanmasına izin vererek kaostaki evrenselliği keşfettiler .

1979'da Albert J. Libchaber , Aspen'de Pierre Hohenberg tarafından düzenlenen bir sempozyum sırasında , Rayleigh-Bénard konveksiyon sistemlerinde kaosa ve türbülansa yol açan çatallanma çağlayanına ilişkin deneysel gözlemini sundu . İlham veren başarılarından dolayı Mitchell J. Feigenbaum ile birlikte 1986 yılında Wolf Fizik Ödülü'ne layık görüldü .

1986'da New York Bilimler Akademisi, Ulusal Ruh Sağlığı Enstitüsü ve Deniz Araştırmaları Ofisi ile birlikte biyoloji ve tıpta kaos üzerine ilk önemli konferansı düzenledi. Orada, Bernardo Huberman şizofrenler arasındaki göz izleme bozukluğunun matematiksel bir modelini sundu . Bu , 1980'lerde, örneğin patolojik kalp döngülerinin incelenmesinde, kaos teorisinin uygulanması yoluyla fizyolojinin yenilenmesine yol açtı .

1987'de Per Bak , Chao Tang ve Kurt Wiesenfeld , Fiziksel Gözden Geçirme Mektupları'nda , doğada karmaşıklığın ortaya çıktığı mekanizmalardan biri olarak kabul edilen ilk kez kendi kendine organize kritikliği (SOC) açıklayan bir makale yayınladı .

Bak–Tang–Wiesenfeld kum yığını gibi büyük ölçüde laboratuvar temelli yaklaşımların yanı sıra, diğer birçok araştırma, ölçekte değişmeyen davranış gösterdiği bilinen (veya şüphelenilen) büyük ölçekli doğal veya sosyal sistemlere odaklanmıştır . Bu yaklaşımlar (en azından başlangıçta) incelenen konularda uzmanlar tarafından her zaman memnuniyetle karşılanmasa da, SOC yine de depremler de dahil olmak üzere (SOC keşfedilmeden çok önce biliniyordu) bir dizi doğal fenomeni açıklamak için güçlü bir aday olarak kabul edildi. olarak ölçek değişmeyen davranış böyle bir kaynağı olarak Gutenberg-Richter hukukun deprem boyutlarının istatistiksel dağılımı açıklayan ve Omori hukuk artçı sıklığını açıklayan), güneş patlamaları gibi ekonomik sistemler dalgalanmalara mali piyasalar (SOC referans olan ekonofizikte ortaktır ), peyzaj oluşumu, orman yangınları , toprak kaymaları , salgın hastalıklar ve biyolojik evrim (burada SOC, örneğin Niles Eldredge ve Stephen Jay Gould tarafından öne sürülen " noktalı dengeler " teorisinin arkasındaki dinamik mekanizma olarak çağrılmıştır ) . Olay boyutlarının ölçeksiz dağılımının etkileri göz önüne alındığında, bazı araştırmacılar SOC örneği olarak düşünülmesi gereken başka bir olgunun savaşların meydana gelmesi olduğunu öne sürdüler . SOC'nin bu araştırmaları, hem modelleme (yeni modeller geliştirme veya mevcut olanları belirli bir doğal sistemin özelliklerine uyarlama) girişimlerini hem de doğal ölçekleme yasalarının varlığını ve/veya özelliklerini belirlemek için kapsamlı veri analizini içeriyordu.

Aynı yıl, James Gleick en çok satan kitap haline gelen ve tarihi önemli Sovyet katkılarını yeterince vurgulamasa da kaos teorisinin genel ilkelerini ve tarihini geniş kamuoyuna tanıtan Kaos: Yeni Bir Bilim Üretmek adlı kitabını yayınladı . Başlangıçta birkaç izole bireyin alanı olan kaos teorisi, giderek disiplinler arası ve kurumsal bir disiplin olarak, esas olarak doğrusal olmayan sistem analizi adı altında ortaya çıktı . Thomas Kuhn'un Bilimsel Devrimlerin Yapısı'nda (1962) açığa çıkan bir paradigma kayması kavramına atıfta bulunarak , birçok "kaolog" (bazılarının kendilerini tanımladığı gibi), bu yeni teorinin böyle bir kaymanın bir örneği olduğunu, Gleick tarafından onaylanan bir tez olduğunu iddia etti. .

Daha ucuz, daha güçlü bilgisayarların mevcudiyeti, kaos teorisinin uygulanabilirliğini genişletiyor. Şu anda, kaos teorisi matematik , topoloji , fizik , sosyal sistemler , nüfus modelleme , biyoloji , meteoroloji , astrofizik , bilgi teorisi , hesaplamalı sinirbilim , pandemik kriz yönetimi vb. gibi birçok farklı disiplini içeren aktif bir araştırma alanı olmaya devam etmektedir .

Uygulamalar

Görünüş olarak Kural 30'a benzeyen bir konus tekstil kabuğu, kaotik davranışa sahip bir hücresel otomat .

Kaos teorisi hava modellerini gözlemlemekten doğmuş olsa da, çeşitli diğer durumlara uygulanabilir hale geldi. Günümüzde kaos teorisinden yararlanan bazı alanlar jeoloji , matematik , biyoloji , bilgisayar bilimi , ekonomi , mühendislik , finans , algoritmik ticaret , meteoroloji , felsefe , antropoloji , fizik , politika , nüfus dinamiği , psikoloji ve robotiktir . Birkaç kategori aşağıda örneklerle listelenmiştir, ancak yeni uygulamalar ortaya çıktığı için bu kesinlikle kapsamlı bir liste değildir.

kriptografi

Kaos teorisi kriptografide uzun yıllardır kullanılmaktadır . Son birkaç on yılda, yüzlerce kriptografik ilkel tasarımında kaos ve doğrusal olmayan dinamikler kullanılmıştır . Bu algoritmalar, görüntü şifreleme algoritmalarını , karma işlevleri , güvenli sözde rastgele sayı üreteçlerini , akış şifrelerini , filigranlamayı ve steganografiyi içerir . Bu algoritmaların çoğu tek modlu kaotik haritalara dayalıdır ve bu algoritmaların büyük bir kısmı anahtar olarak kontrol parametrelerini ve kaotik haritaların başlangıç ​​durumunu kullanır. Daha geniş bir perspektiften, genelliği kaybetmeden, kaotik haritalar ve kriptografik sistemler arasındaki benzerlikler, kaos tabanlı kriptografik algoritmaların tasarımı için ana motivasyondur. Bir tür şifreleme, gizli anahtar veya simetrik anahtar , kaos teorisi tarafından iyi bir şekilde modellenen difüzyon ve karışıklığa dayanır . Başka bir hesaplama türü olan DNA hesaplaması , kaos teorisi ile eşleştirildiğinde, görüntüleri ve diğer bilgileri şifrelemek için bir yol sunar. DNA-Kaos kriptografik algoritmalarının çoğunun ya güvenli olmadığı kanıtlanmıştır ya da uygulanan tekniğin verimli olmadığı ileri sürülmektedir.

robotik

Robotik, son zamanlarda kaos teorisinden yararlanan başka bir alandır. Çevreleriyle etkileşime geçmek için deneme yanılma türünde bir iyileştirmede hareket eden robotlar yerine, tahmine dayalı bir model oluşturmak için kaos teorisi kullanılmıştır . Kaotik dinamikler, pasif yürüyen iki ayaklı robotlar tarafından sergilenmiştir .

Biyoloji

Yüz yılı aşkın bir süredir biyologlar, popülasyon modelleriyle farklı türlerin popülasyonlarını takip ediyor . Çoğu model süreklidir , ancak son zamanlarda bilim adamları belirli popülasyonlarda kaotik modelleri uygulayabildiler. Örneğin, Kanada vaşağı modelleri üzerine yapılan bir araştırma , nüfus artışında kaotik bir davranış olduğunu gösterdi. Kaos, hidroloji gibi ekolojik sistemlerde de bulunabilir . Hidroloji için kaotik bir modelin eksiklikleri olsa da, verilere kaos teorisi merceğinden bakmaktan hala öğrenilecek çok şey var. Başka bir biyolojik uygulama kardiyotokografide bulunur . Fetal sürveyans, mümkün olduğu kadar invaziv olmamakla birlikte doğru bilgi edinmenin hassas bir dengesidir. Kaotik modelleme yoluyla fetal hipoksi uyarı işaretleri için daha iyi modeller elde edilebilir.

ekonomi

Ekonomik modellerin kaos teorisinin uygulanması yoluyla da geliştirilebilmesi mümkündür, ancak bir ekonomik sistemin sağlığını ve onu en çok hangi faktörlerin etkilediğini tahmin etmek son derece karmaşık bir iştir. Ekonomik ve finansal sistemler, klasik doğa bilimlerindeki sistemlerden temel olarak farklıdır, çünkü birincisi, doğası gereği stokastiktir, çünkü bunlar insanların etkileşimlerinden kaynaklanır ve bu nedenle saf deterministik modellerin verilerin doğru temsillerini sağlaması olası değildir. Ekonomi ve finansta kaosu test eden ampirik literatür, kısmen, belirli kaos testleri ile doğrusal olmayan ilişkiler için daha genel testler arasındaki karışıklıktan dolayı çok karışık sonuçlar sunmaktadır.

Ekonomide kaos, yineleme niceleme analizi yoluyla bulunabilir . Aslında, Orlando ve ark. sözde nüks niceleme korelasyon indeksi vasıtasıyla zaman serilerindeki gizli değişiklikleri tespit edebildiler. Daha sonra, aynı teknik, laminer (yani düzenli) evrelerden türbülanslı (yani kaotik) evrelere geçişleri ve ayrıca makroekonomik değişkenler arasındaki farklılıkları tespit etmek ve ekonomik dinamiklerin gizli özelliklerini vurgulamak için kullanıldı. Son olarak, kaos, ekonominin nasıl işlediğini modellemenin yanı sıra COVID-19 gibi dış olaylardan kaynaklanan şokları yerleştirmede yardımcı olabilir. Araçlar ve deterministik kaotik modellerin (örneğin Kaldor-Kalecki, Goodwin, Harrod) ampirik olarak kalibre edilmesi ve test edilmesiyle elde edilen sonuçlar hakkında güncellenmiş bir açıklama için, bakınız Orlando ve ark.

Diğer alanlar

Kimyada, gaz çözünürlüğünü tahmin etmek polimer üretimi için esastır , ancak parçacık sürüsü optimizasyonu (PSO) kullanan modeller yanlış noktalara yaklaşma eğilimindedir. Simülasyonların takılıp kalmasını önleyen kaos tanıtılarak geliştirilmiş bir PSO sürümü oluşturuldu. Gelen gök mekaniği , özellikle, asteroitler gözlemleyerek zaman bu nesneler Dünya ve diğer gezegenleri yaklaşacaktır zaman daha iyi tahminlerine kaos teorisi yol uygulamak. Plüton'un beş uydusundan dördü düzensiz bir şekilde dönüyor. Olarak kuantum fizik ve elektrik mühendisliği , büyük dizilerin çalışma Josephson eklemlerinin kaos teorisi büyük ölçüde yararlanmıştır. Eve daha yakın olan kömür madenleri, sık sık doğal gaz sızıntılarının birçok ölüme neden olduğu her zaman tehlikeli yerler olmuştur. Yakın zamana kadar, ne zaman ortaya çıkacaklarını tahmin etmenin güvenilir bir yolu yoktu. Ancak bu gaz sızıntıları, uygun şekilde modellendiğinde oldukça doğru bir şekilde tahmin edilebilecek kaotik eğilimlere sahiptir.

Kaos teorisi doğa bilimlerinin dışında uygulanabilir, ancak tarihsel olarak bu tür çalışmaların neredeyse tamamı tekrarlanabilirlik eksikliğinden muzdariptir; zayıf dış geçerlilik; ve/veya çapraz doğrulamaya dikkatsizlik, bu da zayıf tahmin doğruluğuna neden olur (örnek dışı tahmin bile denendiyse). Glass ve Mandell ve Selz, hiçbir EEG çalışmasının henüz garip çekicilerin veya diğer kaotik davranış belirtilerinin varlığını göstermediğini buldular.

Araştırmacılar kaos teorisini psikolojiye uygulamaya devam ettiler. Örneğin, Wilfred Bion'un teorisindeki temel varsayımı farklı derecelerde paylaşıyormuş gibi heterojen üyelerin davranabileceği grup davranışını modellemede , araştırmacılar grup dinamiğinin üyelerin bireysel dinamiklerinin sonucu olduğunu bulmuşlardır: her biri birey grup dinamiklerini farklı bir ölçekte yeniden üretir ve grubun kaotik davranışı her üyeye yansır.

Redington ve Reidbord (1992), insan kalbinin kaotik özellikler gösterebileceğini göstermeye çalıştı. Bir terapi seansı sırasında değişen duygusal yoğunluk dönemlerinden geçerken tek bir psikoterapi hastası için kalp atışı aralıklarındaki değişiklikleri izlediler. Sonuçlar kuşkusuz yetersizdi. Yazarların yalnızca kaotik dinamiklerin kanıtlarını (spektral analiz, faz yörüngesi ve otokorelasyon çizimleri) göstermek için ürettikleri çeşitli grafiklerde belirsizlikler yoktu, aynı zamanda kaotik davranışın daha kesin bir teyidi olarak bir Lyapunov üssü hesaplamaya çalıştıklarında, yazarlar bunu güvenilir bir şekilde yapamayacaklarını gördüler.

1995 tarihli makalelerinde Metcalf ve Allen, hayvan davranışında, kaosa yol açan bir dönem iki katına çıkma modelini ortaya çıkardıklarını ileri sürdüler. Yazarlar, belirli bir süre boyunca yiyecekten yoksun bırakılan bir hayvanın, yiyecek en sonunda sunulduğunda olağandışı miktarlarda su içeceği, programa bağlı polidipsi adı verilen iyi bilinen bir yanıtı inceledi. Burada çalışan kontrol parametresi (r), bir kez devam ettirildiğinde beslemeler arasındaki aralığın uzunluğuydu. Yazarlar, çok sayıda hayvanı test etmeye ve birçok tekrarı dahil etmeye özen gösterdiler ve deneylerini, tepki modellerindeki değişikliklerin r için farklı başlangıç ​​yerlerinden kaynaklanma olasılığını ortadan kaldıracak şekilde tasarladılar.

Zaman serileri ve ilk gecikme grafikleri, besleme süreleri arttıkça periyodiklikten düzensizliğe oldukça açık bir yürüyüş gösteren iddialar için en iyi desteği sağlar. Öte yandan, çeşitli faz yörünge çizimleri ve spektral analizler, diğer grafiklerle veya genel teori ile amansız bir şekilde kaotik bir teşhise yol açacak kadar iyi uyuşmamaktadır. Örneğin, faz yörüngeleri gittikçe daha fazla karmaşıklığa doğru (ve periyodiklikten uzak) kesin bir ilerleme göstermemektedir; süreç oldukça bulanık görünüyor. Ayrıca, Metcalf ve Allen'ın spektral planlarında iki ve altı periyotları gördükleri yerde, alternatif yorumlar için yer var. Tüm bu belirsizlik, sonuçların kaotik bir modele uyduğunu göstermek için bazı serpantin, post-hoc açıklamaları gerektiriyor.

Amundson ve Bright, bir kariyer danışmanlığı modelini, çalışanlar ve iş piyasası arasındaki ilişkinin kaotik bir yorumunu içerecek şekilde uyarlayarak, kariyer kararlarıyla mücadele eden insanlara daha iyi önerilerde bulunulabileceğini keşfettiler. Modern organizasyonlar, giderek artan bir şekilde, kaosa katkıda bulunabilecek iç ve dış güçlere tabi, temel doğal doğrusal olmayan yapılara sahip , açık karmaşık uyarlanabilir sistemler olarak görülmektedir . Örneğin , ilk kez karşılaşan farklı bireylerin belirsizliği ekibin gidişatını bilinmez hale getirdiğinden , ekip oluşturma ve grup geliştirme , doğası gereği öngörülemeyen bir sistem olarak giderek daha fazla araştırılmaktadır.

Bazıları, matematiksel modellere ve insan davranışının psikolojik yönlerine dayanan -sözlü teorilerde kullanılan- kaos metaforunun, metaforun kendisinin ötesine geçen küçük çalışma gruplarının karmaşıklığını tanımlamaya yardımcı içgörüler sağladığını söylüyor.

Trafik tahmini, kaos teorisinin uygulamalarından yararlanabilir. Trafiğin ne zaman meydana geleceğine dair daha iyi tahminler, trafiğin meydana gelmeden önce dağıtılması için önlemler alınmasını sağlayacaktır. Kaos teorisi ilkelerini birkaç başka yöntemle birleştirmek, daha doğru bir kısa vadeli tahmin modeline yol açmıştır (sağdaki BML trafik modeli grafiğine bakın).

Kaos teorisi, yağış ve akarsu akışı gibi çevresel su döngüsü verilerine (diğer adıyla hidrolojik veriler) uygulanmıştır. Bu çalışmalar tartışmalı sonuçlar vermiştir, çünkü kaotik bir imzayı tespit etme yöntemleri genellikle nispeten özneldir. İlk çalışmalar kaos bulmada "başarılı" olma eğilimindeyken, sonraki çalışmalar ve meta-analizler bu çalışmaları sorguladı ve bu veri kümelerinin neden düşük boyutlu kaotik dinamiklere sahip olma olasılığının olmadığına dair açıklamalar sağladı.

Ayrıca bakınız

kaotik sistem örnekleri

Diğer ilgili konular

İnsanlar

Referanslar

daha fazla okuma

Nesne

• Sharkovski, AN (1964). "Çizginin kendi içine sürekli haritalanmasının döngülerinin bir arada bulunması". Ukraynalı Matematik. J . 16 : 61-71.
• Li, TY ; Yorke, JA (1975). "Üçüncü Dönem Kaosu İma Eder" (PDF) . Amerikan Matematiksel Aylık . 82 (10): 985-92. Bibcode : 1975AmMM...82..985L . CiteSeerX  10.1.1.329.5038 . doi : 10.2307/2318254 . JSTOR  2318254 . Orijinalinden (PDF) 2009-12-29 tarihinde arşivlendi . 2009-08-12 alındı .
• Alemansur, Hamed; Miandoab, Ehsan Maani; Pişkenari, Hüseyin Nejat (Mart 2017). "Nano rezonatörlerin kaotik davranışı üzerinde boyutun etkisi". Doğrusal Olmayan Bilimde İletişim ve Sayısal Simülasyon . 44 : 495-505. Bibcode : 2017CNSNS..44..495A . doi : 10.1016/j.cnsns.2016.09.010 .
• koltuk değneği ; Tucker; Morrison; JD Çiftçi ; Paket ; NH; Shaw ; RS (Aralık 1986). "Kaos". Bilimsel Amerikalı . 255 (6): 38–49 (kaynakça s.136). Bibcode : 1986SciAm.255d..38T . doi : 10.1038/scientificamerican1286-46 . Çevrimiçi sürüm (Not: çevrimiçi metin için belirtilen cilt ve sayfa alıntısı burada belirtilenden farklıdır. Buradaki alıntı, çevrimiçi bulunan ve makale görünümü sağlamayan diğer alıntılarla tutarlı olan bir fotokopiden yapılmıştır. Çevrimiçi içerik aynıdır. basılı metne. Alıntı varyasyonları yayınlandığı ülkeyle ilgilidir).
• Kolyada, SF (2004). "Li-Yorke duyarlılığı ve diğer kaos kavramları". Ukraynalı Matematik. J . 56 (8): 1242–57. doi : 10.1007/s11253-005-0055-4 . S2CID  207251437 .
• Gün, Sağ; Pavlov, OV (2004). "Bilgisayar Ekonomik Kaos". Hesaplamalı Ekonomi . 23 (4): 289–301. doi : 10.1023/B:CSEM.0000026787.81469.1f . S2CID  119972392 . SSRN  806124 .
• Strelioff, C.; Hübler, A. (2006). "Kaosun Orta Vadeli Tahmini" (PDF) . Fizik Rev. Lett . 96 (4): 044101. Bibcode : 2006PhRvL..96d4101S . doi : 10.1103/PhysRevLett.96.044101 . PMID  16486826 . 044101. Arşivlenmiş orijinal (PDF) 2013-04-26 tarihinde.
• Hübler, A.; Foster, G.; Phelps, K. (2007). "Kaosu Yönetmek: Alışılmışın Dışında Düşünmek" (PDF) . Karmaşıklık . 12 (3): 10-13. Bibcode : 2007Cmplx..12c..10H . doi : 10.1002/cplx.20159 . Arşivlenmiş orijinal (PDF) 2012-10-30 tarihinde . 2011-07-17 alındı .
• Motter, Adilson E.; Campbell, David K. (2013). "50'de Kaos". Fizik Bugün . 66 (5): 27. arXiv : 1306.5777 . Bibcode : 2013PhT....66e..27M . doi : 10.1063/PT.3.1977 . S2CID  54005470 .

ders kitapları

• Alligood, KT; Sauer, T.; Yorke, JA (1997). Kaos: dinamik sistemlere giriş . Springer-Verlag. ISBN'si 978-0-387-94677-1.
• Baker, GL (1996). Kaos, Saçılma ve İstatistiksel Mekanik . Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-39511-3.
• Badii, R.; Politi A. (1997). Karmaşıklık: fizikte hiyerarşik yapılar ve ölçekleme . Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-66385-4.
• Bunde; Havlin, Shlomo , ed. (1996). Fraktallar ve Düzensiz Sistemler . Springer. ISBN'si 978-3642848704.ve Bunde; Havlin, Shlomo , ed. (1994). Bilimde Fraktallar . Springer. ISBN'si 978-3-540-56220-7.
• Collet, Pierre ve Eckmann, Jean-Pierre (1980). Dinamik Sistemler Olarak Aralıkta Yinelenen Haritalar . Birkhauser. ISBN'si 978-0-8176-4926-5.CS1 bakımı: birden çok ad: yazar listesi ( bağlantı )
• Devaney, Robert L. (2003). Kaotik Dinamik Sistemlere Giriş (2. baskı). Westview Basın. ISBN'si 978-0-8133-4085-2.
• Robinson, Clark (1995). Dinamik sistemler: Kararlılık, sembolik dinamikler ve kaos . CRC Basın. ISBN'si 0-8493-8493-1.
• Feldman, DP (2012). Kaos ve Fraktallar: Temel Bir Giriş . Oxford Üniversitesi Yayınları. ISBN'si 978-0-19-956644-0.
• Gollub, JP; Baker, GL (1996). Kaotik dinamikler . Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-47685-0.
• Guckenheimer, John ; Holmes, Philip (1983). Doğrusal Olmayan Salınımlar, Dinamik Sistemler ve Vektör Alanlarının Çatallanmaları . Springer-Verlag. ISBN'si 978-0-387-90819-9.
• Gulick, Denny (1992). Kaos ile Karşılaşır . McGraw-Hill. ISBN'si 978-0-07-025203-5.
• Gutzwiller, Martin (1990). Klasik ve Kuantum Mekaniğinde Kaos . Springer-Verlag. ISBN'si 978-0-387-97173-5.
• Hoover, William Graham (2001) [1999]. Zaman Tersinirliği, Bilgisayar Simülasyonu ve Kaos . Dünya Bilimsel. ISBN'si 978-981-02-4073-8.
• Kautz, Richard (2011). Kaos: Öngörülebilir Rastgele Hareket Bilimi . Oxford Üniversitesi Yayınları. ISBN'si 978-0-19-959458-0.
• Kiel, L. Douglas; Elliott, Euel W. (1997). Sosyal Bilimlerde Kaos Teorisi . Perseus Yayıncılık. ISBN'si 978-0-472-08472-2.
• Ay, Francis (1990). Kaotik ve Fraktal Dinamikler . Springer-Verlag. ISBN'si 978-0-471-54571-2.
• Orlando, Giuseppe ; Pisarchick, İskender; Dur, Ruedi. "İktisatta Doğrusal Olmayanlar | SpringerLink" . doi : 10.1007/978-3-030-70982-2 . Alıntı günlüğü gerektirir |journal=( yardım )
• Ott, Edward (2002). Dinamik Sistemlerde Kaos . Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-01084-9.
• Strogatz, Steven (2000). Doğrusal Olmayan Dinamikler ve Kaos . Perseus Yayıncılık. ISBN'si 978-0-7382-0453-6.
• Sprott, Julien Clinton (2003). Kaos ve Zaman Serisi Analizi . Oxford Üniversitesi Yayınları. ISBN'si 978-0-19-850840-3.
• Tel, Tamas; Gruiz, Márton (2006). Kaotik dinamikler: Klasik mekaniğe dayalı bir giriş . Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-83912-9.
• Teschl, Gerald (2012). Adi Diferansiyel Denklemler ve Dinamik Sistemler . Providence : Amerikan Matematik Derneği . ISBN'si 978-0-8218-8328-0.
• Thompson JM, Stewart HB (2001). Doğrusal Olmayan Dinamikler ve Kaos . John Wiley and Sons Ltd. ISBN 978-0-471-87645-8.
• Tufilaro ; Reilly (1992). Doğrusal olmayan dinamiklere ve kaosa deneysel bir yaklaşım . Amerikan Fizik Dergisi . 61 . Addison-Wesley. P. 958. Bibcode : 1993AmJPh..61..958T . doi : 10.1119/1.17380 . ISBN'si 978-0-201-55441-0.
• Wiggins, Stephen (2003). Uygulamalı Dinamik Sistemlere ve Kaosa Giriş . Springer. ISBN'si 978-0-387-00177-7.
• Zaslavsky, George M. (2005). Hamilton Kaosu ve Kesirli Dinamikler . Oxford Üniversitesi Yayınları. ISBN'si 978-0-19-852604-9.

Yarı teknik ve popüler eserler

• Christophe Letellier , Doğada Kaos , World Scientific Publishing Company, 2012, ISBN  978-981-4374-42-2 .
• İbrahim, Ralph; et al. (2000). Abraham, Ralph H.; Ueda, Yoshisuke (der.). Kaos Avangard: Kaos Teorisinin İlk Günlerinin Anıları . Doğrusal Olmayan Bilim Serileri Üzerine Dünya Bilimsel Serileri A. 39 . Dünya Bilimsel. Bibcode : 2000cagm.book.....A . doi : 10.1142/4510 . ISBN'si 978-981-238-647-2.
• Barnsley, Michael F. (2000). Fraktallar Her Yerde . Morgan Kaufmann. ISBN'si 978-0-12-079069-2.
• Kuş, Richard J. (2003). Kaos ve Yaşam: Evrim ve Düşüncede Karmaşıklık ve Düzen . Columbia Üniversitesi Yayınları. ISBN'si 978-0-231-12662-5.
• John Briggs ve David Peat, Turbulent Mirror: : An Illustrated Guide to Chaos Theory and the Science of Wholeness , Harper Perennial 1990, 224 s.
• John Briggs ve David Peat, Kaosun Yedi Hayat Dersi: Değişim Biliminden Manevi Bilgelik , Harper Perennial 2000, 224 s.
• Cunningham, Lawrence A. (1994). "Rastgele Yürüyüşlerden Kaotik Çöküşlere: Etkin Sermaye Piyasası Hipotezinin Doğrusal Soykütüğü". George Washington Hukuku İnceleme . 62 : 546.
• Predrag Cvitanović , Kaosta Evrensellik , Adam Hilger 1989, 648 s.
• Leon Glass ve Michael C. Mackey, Saatlerden Kaosa: Hayatın Ritimleri, Princeton University Press 1988, 272 s.
• James Gleick , Chaos: Making a New Science , New York: Penguin, 1988. 368 s.
• John Gribbin. Derin Sadelik . Penguen Basın Bilimi. Penguen Kitapları.
• L Douglas Kiel, Euel W Elliott (ed.), Sosyal Bilimlerde Kaos Teorisi: Temeller ve Uygulamalar , University of Michigan Press, 1997, 360 s.
• Arvind Kumar, Kaos, Fraktallar ve Öz Örgütlenme; Doğada Karmaşıklık Üzerine Yeni Perspektifler , National Book Trust, 2003.
• Hans Lauwerier, Fraktallar , Princeton University Press, 1991.
• Edward Lorenz , The Essence of Chaos , University of Washington Press, 1996.
• Marshall, Alan (2002). Ekoloji ve Bilimde Doğanın Birliği - Bütünlük ve Parçalanma . doi : 10.1142/9781860949548 . ISBN'si 9781860949548.
• David Peak ve Michael Frame, Kaos Kontrol Altında: Karmaşıklığın Sanatı ve Bilimi , Freeman, 1994.
• Heinz-Otto Peitgen ve Dietmar Saupe (Ed.), Fraktal Görüntülerin Bilimi , Springer 1988, 312 s.
• Clifford A. Pickover , Bilgisayarlar, Desen, Kaos ve Güzellik: Görünmeyen Bir Dünyadan Grafikler , St Martins Pr 1991.
• Clifford A. Pickover , Harikalar Diyarında Kaos: Fraktal Bir Dünyada Görsel Maceralar , St Martins Pr 1994.
• Ilya Prigogine ve Isabelle Stengers , Kaostan Çıkan Düzen , Bantam 1984.
• Peitgen, Heinz-Otto; Richter, Peter H. (1986). Fraktalların Güzelliği . doi : 10.1007/978-3-642-61717-1 . ISBN'si 978-3-642-61719-5.
• David Ruelle , Şans ve Kaos , Princeton University Press 1993.
• Ivars Peterson , Newton'un Saati: Güneş Sisteminde Kaos , Freeman, 1993.
• Ian Roulstone; John Norbury (2013). Fırtınada Görünmez: Hava durumunu anlamada matematiğin rolü . Princeton Üniversitesi Yayınları. ISBN'si 978-0691152721.
• Ruelle, D. (1989). Kaotik Evrim ve Garip Çekiciler . doi : 10.1017/CBO9780511608773 . ISBN'si 9780521362726.
• Manfred Schroeder, Fraktallar, Kaos ve Güç Kanunları , Freeman, 1991.
• Smith, Peter (1998). Kaosu Anlatmak . doi : 10.1017/CBO9780511554544 . ISBN'si 9780511554544.
• Ian Stewart , Tanrı Zar Oynar mı?: Kaos Matematiği , Blackwell Publishers, 1990.
• Steven Strogatz , Sync: Ortaya çıkan kendiliğinden düzen bilimi , Hyperion, 2003.
• Yoshisuke Ueda, Kaosa Giden Yol , Aerial Pr, 1993.
• M. Mitchell Waldrop, Karmaşıklık : Düzen ve Kaos Kenarında Yükselen Bilim , Simon & Schuster, 1992.
• Antonio Sawaya, Finansal Zaman Serisi Analizi : Kaos ve Nörodinamik Yaklaşım , Lambert, 2012.

Dış bağlantılar

• "Kaos" , Matematik Ansiklopedisi , EMS Press , 2001 [1994]
• Flash'ta Animasyonlu Doğrusal Olmayan Dinamikler Araştırma Grubu
• Maryland Üniversitesi'ndeki Kaos grubu
• Kaos Hipermetin Kitabı . Kaos ve fraktallar üzerine bir giriş kitabı
• ChaosBook.org Kaos üzerine ileri düzey bir lisansüstü ders kitabı ( fraktal yok)
• Psikoloji ve Yaşam Bilimlerinde Kaos Teorisi Derneği
• CSDC'de Doğrusal Olmayan Dinamikler Araştırma Grubu , Floransa İtalya
• Etkileşimli canlı kaotik sarkaç deneyi , kullanıcıların etkileşime girmesine ve gerçek bir çalışma sönümlü tahrikli kaotik sarkaçtan veri örneklemesine olanak tanır
• Doğrusal olmayan dinamikler: bilimin kaosu nasıl kavradığı, Sunny Auyang, 1998 tarafından sunulan konuşma.
• Doğrusal Olmayan Dinamikler . Elmer G. Wiens tarafından çatallanma ve kaos modelleri
• Gleick's Chaos (alıntı) 2007-02-02 tarihinde Wayback Machine'de Arşivlendi
• Oxford Üniversitesi'nde Sistem Analizi, Modelleme ve Tahmin Grubu
• Mackey-Glass denklemi hakkında bir sayfa
• Yüksek Kaygılar - Kaos'un Matematiği (2008) David Malone tarafından yönetilen BBC belgeseli
• Evrimin kaos teorisi - Newscientist'te yayınlanan, yaşamın fraktal doğası ve kaos dahil olmak üzere evrim ve doğrusal olmayan sistemler arasındaki benzerlikleri içeren makale.
• Jos Leys, Étienne Ghys ve Aurélien Alvarez, Kaos, Matematiksel Bir Macera . Dinamik sistemler, kelebek etkisi ve kaos teorisi hakkında geniş bir izleyici kitlesine yönelik dokuz film.
• "Kaos Teorisi" , Susan Greenfield, David Papineau ve Neil Johnson ile BBC Radio 4 tartışması ( In Our Time , 16 Mayıs 2002)
• Chaos: The Science of the Butterfly Effect (2019) Derek Muller tarafından sunulan bir açıklama