Düzenli çokgen - Regular polygon

Dışbükey düzenli n-gonlar kümesi
düzgün çokgenler
Kenarlar ve köşeler	n
Schläfli sembolü	{ n }
Coxeter-Dynkin diyagramı
simetri grubu	D , n , sipariş 2n
Çift çokgen	Kendinden çift
Alan (kenar uzunluklu, s )	${\displaystyle A={\tfrac {1}{4}}ns^{2}\cot \left({\frac {\pi }{n}}\sağ)}$
İç açı	${\displaystyle (n-2)\times {\frac {180^{\circ }}{n}}}$
İç açı toplamı	${\displaystyle \sol(n-2\sağ)\times 180^{\circ }}$
Yazılı daire çapı	${\displaystyle d_{\text{IC}}=s\cot \left({\frac {\pi }{n}}\sağ)}$
Çevrelenmiş daire çapı	${\displaystyle d_{\text{OC}}=s\csc \left({\frac {\pi }{n}}\sağ)}$
Özellikler	Dışbükey , döngüsel , eşkenar , izogonal , izotoksal

Gelen Öklid geometrisi , bir düzgün poligon a, çokgen olan eşit açılı ve (tüm açılar ölçüde eşittir) eşkenar (bütün kenarları aynı uzunluğa sahip). Düzenli çokgenler dışbükey veya yıldız olabilir . Olarak sınırı , iki giderek artan sayıda düzenli çokgen bir sekans, bir yaklaşır daire ise, çevre veya alan sabit veya düzenli apeirogon (özellikle bir düz çizgi ), kenar uzunluğu sabitleştirilmesi tercih edilir.

Genel Özellikler

Schläfli sembolleriyle etiketlenmiş 3 ila 12 köşeli düzenli dışbükey ve yıldız çokgenler

Bu özellikler, ister dışbükey ister yıldız olsun, tüm düzgün çokgenler için geçerlidir .

Normal bir n kenarlı çokgen, n düzeninde dönme simetrisine sahiptir .

Düzgün bir çokgenin tüm köşeleri ortak bir daire ( sınırlandırılmış daire ) üzerinde bulunur; yani bunlar konsiklik noktalardır . Yani, düzenli bir çokgen, döngüsel bir çokgendir .

Birlikte, eşit uzunlukta iki özelliği ile, bu her düzgün poligon da bir yazılı daire ya da sahip olduğu ima incircle orta noktasında her tarafında teğet olduğu. Böylece düzgün bir çokgen teğet bir çokgendir .

Düzgün bir n kenarlı çokgen, yalnızca ve ancak n'nin tek asal çarpanları farklı Fermat asallarıysa , pergel ve cetvelle oluşturulabilir . Bkz. inşa edilebilir çokgen .

Simetri

Simetri grubu , bir bölgesinin n düzgün poligon olduğu taraflı dihedral grubu D _{, n} (2 seviyesinde n ): D ₂ , D ₃ , D ₄ , ... Bu C dönüş oluşur _N ile birlikte, yansıma simetri içinde n eksen bu merkezden geçer. Eğer n çift ise, bu eksenlerin yarısı iki zıt köşeden, diğer yarısı da zıt kenarların ortasından geçer. Eğer n, tek bir sonra tüm eksenleri bir tepe ve karşı tarafta orta noktası geçer.

Düzenli dışbükey çokgenler

Tüm normal basit çokgenler (basit bir çokgen, kendisini hiçbir yerde kesmeyen bir çokgendir) dışbükeydir. Kenar sayıları aynı olanlar da benzerdir .

Bir n kenarlı dışbükey düzenli çokgen, Schläfli sembolü { n } ile gösterilir. For n <3, iki sahip dejenere durumları:

monogon {1}

Sıradan uzayda dejenere . (Çoğu otorite, kısmen bu nedenle ve ayrıca aşağıdaki formüller çalışmadığı ve yapısı herhangi bir soyut çokgeninki olmadığı için monogonu gerçek bir çokgen olarak görmez .)

Digon {2}; bir "çift hat segmenti"

Sıradan uzayda dejenere . (Bazı otoriteler bu nedenle digonu gerçek bir çokgen olarak görmezler.)

Belirli bağlamlarda, dikkate alınan tüm çokgenler düzenli olacaktır. Bu gibi durumlarda, öneki düzenli olarak bırakmak gelenekseldir. Örneğin, düzgün çokyüzlülerin tüm yüzleri düzgün olmalıdır ve yüzler basitçe üçgen, kare, beşgen vb. olarak tanımlanacaktır.

açılar

Düzgün bir dışbükey n- gon için, her bir iç açının bir ölçüsü vardır:

${\displaystyle {\frac {180(n-2)}{n}}}$ derece;

${\displaystyle {\frac {(n-2)\pi }{n}}}$radyan; veya

${\displaystyle {\frac {(n-2)}{2n}}}$tam dönüşler ,

ve her dış açının (yani, iç açının tamamlayıcısı ), dış açıların toplamı 360 dereceye veya 2π radyana veya bir tam dönüşe eşit olan bir derece ölçüsü vardır . ${\displaystyle {\tfrac {360}{n}}}$

Olarak N sonsuza yaklaşan iç açısı 180 dereceye yaklaştığında. 10.000 kenarlı (bir çokgen ) düzgün çokgen için iç açı 179.964°'dir. Kenar sayısı arttıkça, iç açı 180°'ye çok yaklaşabilir ve çokgenin şekli bir dairenin şekline yaklaşır. Ancak çokgen asla bir daire olamaz. Çevresi fiilen düz bir çizgi haline geleceğinden, iç açının değeri asla tam olarak 180°'ye eşit olamaz. Bu nedenle çember sonsuz sayıda kenarı olan bir çokgen değildir.

köşegenler

İçin n > 2 sayısı, diyagonalleri olduğu ; yani, 0, 2, 5, 9, ..., bir üçgen, kare, beşgen, altıgen için, ... . Diyagonallere 1, 4, 11, 24, ... parçalar halinde poligonu bölmek OEIS :  A007678 . ${\displaystyle {\tfrac {1}{2}}n(n-3)}$

Birim yarıçaplı daire içine yazılan düzgün bir n- gon için, belirli bir tepe noktasından diğer tüm tepe noktalarına (komşu köşeler ve bir köşegenle bağlanan tepeler dahil) olan mesafelerin çarpımı n'ye eşittir .

Uçaktaki noktalar

Normal bir basit için n ile -gon circumradius R ve mesafeler d _i Elimizdeki, köşelerle düzleminde rastgele bir noktadan

${\displaystyle {\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{4}+3R^{4}=\left({\frac {1}{ n}}\sum _{i=1}^{n}d_{i}^{2}+R^{2}\sağ)^{2}.}$

Düzlemdeki rastgele bir noktadan düzenli bir -gonun köşelerine kadar olan mesafelerin daha yüksek güçleri için , eğer ${\görüntüleme stili d_{i}}$${\görüntüleme stili n}$

${\displaystyle S_{n}^{(2m)}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2m}}$,

sonra

${\displaystyle S_{n}^{(2m)}=\left(S_{n}^{(2)}\sağ)^{m}+\sum _{k=1}^{\left\lfloor { \frac {m}{2}}\right\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R^{2k}\left(S_{n}^{(2) )}-R^{2}\sağ)^{k}\sol(S_{n}^{(2)}\sağ)^{m-2k}}$,

ve

${\displaystyle S_{n}^{(2m)}=\sol(S_{n}^{(2)}\sağ)^{m}+\sum _{k=1}^{\sol\lzemin { \frac {m}{2}}\sağ\rfloor }{\frac {1}{2^{k}}}{\binom {m}{2k}}{\binom {2k}{k}}\sol (S_{n}^{(4)}-\left(S_{n}^{(2)}\sağ)^{2}\sağ)^{k}\left(S_{n}^{(2) )}\sağ)^{m-2k}}$,

' den küçük bir pozitif tamsayı nerede . ${\görüntüleme stili m}$${\görüntüleme stili n}$

Eğer normal bir ağırlık merkezi, düzlemde gelişigüzel bir noktası olan mesafedir circumradius ile -gon sonra, ${\görüntüleme stili L}$${\görüntüleme stili n}$${\görüntüleme stili R}$

${\displaystyle \sum _{i=1}^{n}d_{i}^{2m}=n\left(\left(R^{2}+L^{2}\sağ)^{m}+ \sum _{k=1}^{\left\lfloor {\frac {m}{2}}\right\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R ^{2k}L^{2k}\sol(R^{2}+L^{2}\sağ)^{m-2k}\sağ)}$,

nerede = 1, 2, …, . ${\görüntüleme stili m}$${\görüntüleme stili n-1}$

İç noktalar

Düzgün bir n- gon için, herhangi bir iç noktadan n kenarlara olan dik mesafelerin toplamı , özdeyişin n katıdır (özet, merkezden herhangi bir kenara olan uzaklıktır). Bu, n = 3 durumu için Viviani teoreminin bir genellemesidir .

dairesel yarıçap

Kenar s , dairesel yarıçap R ve özdek a ile düzgün beşgen ( n = 5)

Kenar grafikleri ,  s ; özdeyiş ,  a ; ve alan ,  bir bölgesinin normal çokgenler ve n, iki ve circumradius 1, bir baz ,  b a aynı alana sahip dikdörtgen . Yeşil çizgi n = 6 durumunu gösterir .

Circumradius R köşe birine bir düzgün çokgen merkezine kenar uzunluğu ile ilgilidir ler veya apothem a göre

${\displaystyle R={\frac {s}{2\sin \left({\frac {\pi }{n}}\sağ)}}={\frac {a}{\cos \left({\frac {\pi }{n}}\sağ)}}}$

İçin constructible çokgen , cebirsel ifadeler bu ilişkiler için var; bkz. İki merkezli çokgen#Düzenli çokgenler .

Düzgün bir n- gon'un köşelerinden, çembere teğet olan herhangi bir doğruya diklerinin toplamı, çember yarıçapının n katına eşittir .

Düzgün bir n- gon'un köşelerinden çember çemberi üzerindeki herhangi bir noktaya olan uzaklıkların karesi toplamı 2 nR ^2'ye eşittir , burada R çevre yarıçapıdır.

Düzgün bir n -gon'un kenarlarının orta noktalarından çember üzerindeki herhangi bir noktaya olan uzaklıkların karesi toplamı 2 nR ² −1/4ns ² , burada s kenar uzunluğudur ve R dairesel yarıçaptır.

Eğer düzenli köşeleri arasındaki mesafelerdir kendi circumcircle herhangi bir noktaya -gon sonra, ${\görüntüleme stili d_{i}}$${\görüntüleme stili n}$

${\displaystyle 3\left(\sum _{i=1}^{n}d_{i}^{2}\sağ)^{2}=2n\sum _{i=1}^{n}d_{ ben}^{4}}$.

diseksiyonlar

Coxeter , her zonogonun ( karşı kenarları paralel ve eşit uzunlukta olan 2 m'lik bir gon) parçalara ayrılabileceğini veya${\displaystyle {\tbinom {n}{2}}}$1/2m ( m − 1) paralelkenarlar. Bu döşemeler , ortogonal izdüşümler m -küplerinde köşelerin, kenarların ve yüzlerin alt kümeleri olarak bulunur . Özellikle bu, eşit sayıda kenarı olan düzgün çokgenler için geçerlidir, bu durumda paralelkenarların hepsi eşkenar dörtgendir. Liste OEIS :  A006245 küçük çokgen için çözümlerin sayısını verir.

Seçilmiş çift taraflı düzenli çokgenler için örnek diseksiyonlar

2 m	6	8	10	12	14	16	18	20	24	30	40	50
resim
eşkenar dörtgen	3	6	10	15	21	28	36	45	66	105	190	300

Alan

Alan A dışbükey normal bir N taraflı çokgen olan sahibi s , circumradius R , apothem bir ve çevre s verilir

${\displaystyle A={\tfrac {1}{2}}nsa={\tfrac {1}{2}}pa={\tfrac {1}{4}}ns^{2}\cot \left({ \tfrac {\pi }{n}}\right)=na^{2}\tan \left({\tfrac {\pi }{n}}\right)={\tfrac {1}{2}}nR ^{2}\sin \sol({\tfrac {2\pi }{n}}\sağ)}$

Yan düzenli çokgenler için s = 1, circumradius R = 1 ya da apothem bir = 1, bu aşağıdaki tabloyu üretmektedir: (Not bu yana olarak${\displaystyle \cot x\rightarrow 1/x}$${\displaystyle x\sağ ok 0}$ alan, zaman eğilimi olarak büyük büyür.) ${\görüntüleme stili s=1}$${\görüntüleme stili n^{2}/4\pi }$${\görüntüleme stili n}$

Taraf sayısı	Kenar s = 1 olduğunda alan		Çevresel yarıçap R = 1 olduğunda alan			apothem a = 1 olduğunda alan
	Bire bir aynı	yaklaşıklık	Bire bir aynı	yaklaşıklık	Göreli circumcircle  alana	Bire bir aynı	yaklaşıklık	Göreli incircle  alanının
n	${\displaystyle {\tfrac {n}{4}}\cot \sol({\tfrac {\pi }{n}}\sağ)}$		${\displaystyle {\tfrac {n}{2}}\sin \sol({\tfrac {2\pi }{n}}\sağ)}$		${\displaystyle {\tfrac {n}{2\pi }}\sin \sol({\tfrac {2\pi }{n}}\sağ)}$	${\displaystyle n\tan \sol({\tfrac {\pi }{n}}\sağ)}$		${\displaystyle {\tfrac {n}{\pi }}\tan \sol({\tfrac {\pi }{n}}\sağ)}$
3	${\displaystyle {\tfrac {\sqrt {3}}{4}}}$	0.433012702	${\displaystyle {\tfrac {3{\sqrt {3}}}{4}}}$	1.299038105	0.4134966714	${\displaystyle 3{\sqrt {3}}}$	5.196152424	1.653986686
4	1	1.000000000	2	2.0000000000	0.6366197722	4	4.000000000	1.273239544
5	${\displaystyle {\tfrac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}}$	1.720477401	${\displaystyle {\tfrac {5}{4}}{\sqrt {{\tfrac {1}{2}}\left(5+{\sqrt {5}}\sağ)}}}$	2.377641291	0.7568267288	${\displaystyle 5{\sqrt {5-2{\sqrt {5}}}}}$	3.632712640	1.156328347
6	${\displaystyle {\tfrac {3{\sqrt {3}}}{2}}}$	2.598076211	${\displaystyle {\tfrac {3{\sqrt {3}}}{2}}}$	2.598076211	0,8269933428	${\displaystyle 2{\sqrt {3}}}$	3.464101616	1.102657791
7		3.633912444		2.736410189	0.8710264157		3.371022333	1.073029735
8	${\displaystyle 2+2{\sqrt {2}}}$	4.828427125	${\displaystyle 2{\sqrt {2}}}$	2.828427125	0.9003163160	${\displaystyle 8\sol({\sqrt {2}}-1\sağ)}$	3.313708500	1.054786175
9		6.118824194		2.892544244	0.9207254290		3.275732109	1.042697914
10	${\displaystyle {\tfrac {5}{2}}{\sqrt {5+2{\sqrt {5}}}}}$	7.694208843	${\displaystyle {\tfrac {5}{2}}{\sqrt {{\tfrac {1}{2}}\left(5-{\sqrt {5}}\sağ)}}}$	2.938926262	0.9354892840	${\displaystyle 2{\sqrt {25-10{\sqrt {5}}}}}$	3.249196963	1.034251515
11		9.365639907		2.973524496	0.9465022440		3.229891423	1.028106371
12	${\displaystyle 6+3{\sqrt {3}}}$	11.19615242	3	3.000000000	0.9549296586	${\displaystyle 12\sol(2-{\sqrt {3}}\sağ)}$	3.215390309	1.023490523
13		13.18576833		3.020700617	0.9615188694		3.204212220	1.019932427
14		15.33450194		3.037186175	0.9667663859		3.195408642	1.017130161
15		17.64236291		3.050524822	0.9710122088		3.188348426	1.014882824
16		20.10935797	${\displaystyle 4{\sqrt {2-{\sqrt {2}}}}}$	3.061467460	0.9744953584		3.182597878	1.013052368
17		22.73549190		3.070554163	0.9773877456		3.177850752	1.011541311
18		25.52076819		3.078181290	0.9798155361		3.173885653	1.010279181
19		28.46518943		3.084644958	0.9818729854		3.170539238	1.009213984
20		31.56875757		3.090169944	0.9836316430		3.167688806	1.008306663
100		795.5128988		3.139525977	0,9993421565		3.142626605	1.000329117
1000		79577.20975		3.141571983	0,9999934200		3.141602989	1.000003290
10.000		7957746.893		3.141592448	0,9999999345		3.141592757	1.000000033
1.000.000		79577471545		3.141592654	1.000000000		3.141592654	1.000000000

Aynı kenar uzunluğu normal çokgenler, boyutlarının karşılaştırılması üç için altmış iki. Kenar sayısı sonsuza yaklaştıkça boyut sınırsız olarak artar.

Belirli bir çevreye sahip tüm n- gonlardan en büyük alana sahip olanı düzenlidir.

inşa edilebilir çokgen

Bazı düzgün çokgenleri pergel ve cetvelle oluşturmak kolaydır ; diğer düzgün çokgenler hiç oluşturulamaz. Eski Yunan matematikçiler 3, 4 veya 5 tarafla da düzenli çokgen oluşturmak için nasıl biliyorlardı, ve belirli bir düzenli çokgenin kenarlarının çift sayı ile düzenli çokgen oluşturmak için nasıl biliyordu. Bu, şu sorunun sorulmasına yol açtı: Tüm düzenli n -gonları pusula ve cetvelle oluşturmak mümkün müdür ? Değilse, hangi n- gon'lar inşa edilebilir ve hangileri değildir?

Carl Friedrich Gauss arasında constructibility kanıtladı düzenli 17-gon sonra 1796 Beş yıl içinde, o teorisini geliştirdi Gauss dönemlerde yaptığı yılında Disquisitiones Arithmeticae . Bu teori , düzgün çokgenlerin yapılandırılabilirliği için yeterli bir koşul formüle etmesine izin verdi :

Normal bir n- gon, n , 2'nin bir kuvvetinin ve herhangi bir sayıda farklı Fermat asalının (hiçbiri dahil) ürünüyse, pusula ve cetvelle oluşturulabilir .

(Bir Fermat asal formun bir asal sayısıdır ) Gauss, bu koşulun da gerekli olduğunu kanıtlamadan belirtti , ancak kanıtını hiçbir zaman yayınlamadı. 1837'de Pierre Wantzel tarafından tam bir gereklilik kanıtı verildi . Sonuç Gauss-Wantzel teoremi olarak bilinir . ${\ Displaystyle 2^{(2^{n})}+1.}$

Eşdeğer düzenli n ve ancak eğer köşeli constructible olduğunu kosinüs onun ortak açının bir olan constructible sayı , dört temel aritmetik işlemlerin şart ve kare kökleri çıkarma yazılabilir -yani.

Normal eğri çokgenler

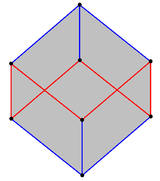Küp bir eğri normal içeren altıgen 6 kırmızı kenarları olarak görülen, zig-zagging küpün çapraz eksenine dik olan iki düzlem arasındaki.

Bir n - antiprizmanın zikzak çizen yan kenarları, bu 17 köşeli antiprizmada gösterildiği gibi, normal bir 2 n -gen eğriliğini temsil eder .

Bir normal eğri çokgen 3-boyutlu uzayda düzlemsel yolları homojen bir yan kenarlar olarak tanımlanan, iki paralel düzlem arasındaki zig-zagging olarak görülebilir antiprizma . Tüm kenarlar ve iç açılar eşittir.

Pluronic katı ( Tetrahedron , küp , oktahedron , dodekahedron ve ikosahedron ) sırasıyla iki 4, 6, 6, 10 ve 10 ile birlikte, burada kırmızı görülen Petrie çokgenler sahiptir.

Daha genel olarak normal eğri çokgenler n- uzayda tanımlanabilir . Örnekler arasında Petrie çokgenleri , düzenli bir politopu iki yarıya bölen ve dik izdüşümde düzenli bir çokgen olarak görülen çokgen kenar yolları bulunur .

Sonsuz limitte normal çarpık çokgenler çarpık apeirogonlar haline gelir .

Düzenli yıldız çokgenler

Düzenli yıldız çokgenler

2 < 2q < p, gcd (p, q) = 1 {5/2} {7/2} {7/3} ...
Schläfli sembolü	{p/q}
Köşeler ve Kenarlar	P
Yoğunluk	Q
Coxeter diyagramı
simetri grubu	Dihedral (D p )
Çift çokgen	Kendinden çift
İç açı ( derece )	${\displaystyle {\frac {180(p-2q)}{p}}}$

Dışbükey olmayan bir düzenli çokgen, normal bir yıldız çokgendir . En yaygın örnek, bir beşgen ile aynı köşelere sahip olan ancak alternatif köşeleri birbirine bağlayan pentagramdır .

n kenarlı bir yıldız çokgen için, Schläfli sembolü , çokgenin yoğunluğunu veya "yıldızlılığını" m gösterecek şekilde değiştirilir , { n / m } olarak. Örneğin m 2 ise, her ikinci nokta birleştirilir. Eğer m, 3, daha sonra, her üç nokta birleştirilmektedir. Çokgenin sınırı, merkez etrafında m kez sarılır.

12 kenarı olan (dejenere olmayan) düzenli yıldızlar şunlardır:

• Pentagram – {5/2}
• Heptagram – {7/2} ve {7/3}
• Sekizgen – {8/3}
• Enneagram – {9/2} ve {9/4}
• Dekagram – { 10/3 }
• Hendecagram – {11/2}, {11/3}, {11/4} ve {11/5}
• Dodecagram – {12/5}

m ve n asal olmalıdır , yoksa şekil bozulur.

12 kenarı olan dejenere düzenli yıldızlar şunlardır:

• Dörtgen – {4/2}
• Altıgenler – {6/2}, {6/3}
• Sekizgenler – {8/2}, {8/4}
• Enneagon – {9/3}
• Ongenler – {10/2}, {10/4} ve {10/5}
• Dodecagons – {12/2}, {12/3}, {12/4} ve {12/6}

{6/2}'nin iki yorumu

Grünbaum {6/2} veya 2{3}	Coxeter 2 {3} veya {6}[2{3}]{6}
Çift yara altıgen	İki üçgenin bir bileşimi olarak heksagram

Schläfli sembolünün kesin olarak türetilmesine bağlı olarak, yozlaşmış figürün doğasına ilişkin görüşler farklıdır. Örneğin, {6/2} iki yoldan biriyle ele alınabilir:

• 20. yüzyılın büyük bir bölümünde (örneğin Coxeter (1948)'e bakınız ), iki üçgenin düzenli bileşimini elde etmek için bir dışbükeyin {6} her bir köşesini iki adım ötedeki yakın komşularına birleştirmeyi belirtmek için genellikle /2'yi aldık. , veya heksagram .
  Coxeter, bu düzenli bileşiği {p/k} bileşiği için bir {kp}[k{p}]{kp} notasyonu ile açıklar, dolayısıyla heksagram {6}[2{3}]{6} olarak temsil edilir. Daha kompakt Coxeter- da yazar 2 {N / 2} gibi 2 olarak bileşik gibi bir heksagramın için {3} alternans gelen faktör italik düzenli çift taraflı çokgen, çakışan yorumlanması ayırmak için.
• Grünbaum (2003) gibi pek çok modern geometri uzmanı bunu yanlış olarak görmektedir. Her adımda {6} çevresinde iki yerin hareket ettiğini belirtmek için /2'yi alırlar, her köşe noktasında üst üste bindirilmiş iki köşesi ve her bir çizgi parçası boyunca iki kenarı olan bir "çift sargılı" üçgen elde ederler. Bu sadece modern soyut politop teorileriyle daha iyi uyum sağlamakla kalmaz, aynı zamanda Poinsot'un (1809) yıldız çokgenlerini yaratma şeklini daha yakından kopyalar - tek bir uzunlukta tel alıp aynı açıyla art arda noktalarda bükerek rakam kapanana kadar.

Düzgün çokgenlerin dualitesi

Tüm düzgün çokgenler eşliğe kendinden çifttir ve tek n için özdeşliğe kendinden çifttir.

Ayrıca düzgün çokgenlerden oluşan düzgün yıldız figürleri (bileşikler) de kendi kendine çifttir.

Çokyüzlülerin yüzleri olarak düzenli çokgenler

Tek tip bir çokyüzlü , yüzler olarak düzenli çokgenlere sahiptir, öyle ki her iki köşe için birini diğerine eşleyen bir izometri vardır (tıpkı normal bir çokgen için olduğu gibi).

Bir yarı-düzenli çokyüzlü , her bir tepe noktasının etrafında değişen sadece iki tür yüze sahip olan tek tip bir çokyüzlüdür.

Bir düzenli polihidron yüzün sadece bir tür olan tek tip bir çok yüzlü olması.

Düzenli yüzleri olan kalan (düzgün olmayan) dışbükey çokyüzlüler Johnson katıları olarak bilinir .

Yüzleri düzgün üçgenlere sahip olan bir çokyüzlüye deltahedron denir .

Ayrıca bakınız

• Dışbükey düzgün çokgenlerle Öklid döşemeleri
• Platonik katı
• Apeirogon – Sonsuz kenarlı bir çokgen ayrıca düzenli olabilir, {∞}.
• Düzenli politoplar ve bileşiklerin listesi
• eşkenar çokgen
• Carlyle çemberi

Notlar

Referanslar

• Coxeter, HSM (1948). "Düzenli Politoplar". Methuen ve Co. Alıntı günlüğü gerektirir |journal=( yardım )
• Grünbaum, B.; Çokyüzlüleriniz benim çokyüzlülerim ile aynı mı?, Ayrık ve hesaplama. geom: Goodman-Pollack festivali , Ed. Aronov ve diğerleri, Springer (2003), s. 461–488.
• Poinsot, L. ; Memoire sur les polygones et polyedres. J. de l'École Polytechnique 9 (1810), s. 16–48.

Dış bağlantılar

• Weisstein, Eric W. "Normal çokgen" . Matematik Dünyası .
• Normal Çokgen açıklaması Etkileşimli animasyonlu
• İnteraktif animasyonlu Normal Çokgen Çemberi
• Normal Çokgen Alanı Etkileşimli animasyonlu üç farklı formül
• Düzenli çokgen Rönesans sanatçıların yapılar at Yakınsama