Pontryagin ikiliği - Pontryagin duality

Matematikte, Pontryagin ikiliği , Fourier dönüşümünün daire grubunu (birin karmaşık sayılarının çarpımsal grubu), sonlu değişmeli grupları ( ayrık topoloji ile ) içeren tüm bu tür gruplara genelleştirilmesine izin veren yerel olarak kompakt değişmeli gruplar arasındaki bir ikiliktir. , ve tam sayıların toplama grubu (ayrık topoloji ile de), gerçek sayılar ve gerçekler veya bir p -adic alanı üzerindeki her sonlu boyutlu vektör uzayı .

Pontryagin çift bir yerel kompakt değişmeli grubunun, sürekli oluşturduğu gruptur grubu homomorfizmalar daire gruptan gruba. Pontryagin ikilik teoremi herhangi yerel kompakt değişmeli grubun Bidual (onun ikili ikili) ile doğal olarak izomorf olduğunu belirterek kurar Pontryagin ikiliği. Fourier inversiyon teoremi bu teoremin özel bir durumudur.

Konunun adı , yerel olarak kompakt değişmeli gruplar teorisinin temellerini ve 1934'teki ilk matematiksel çalışmaları sırasında onların dualitesini ortaya koyan Lev Pontryagin'den almıştır. Pontryagin'in tedavisi, grubun ikinci sayılabilir ve kompakt veya ayrık olmasına dayanıyordu . Bu, 1935'te Egbert van Kampen ve 1940'ta André Weil tarafından genel yerel olarak kompakt değişmeli grupları kapsayacak şekilde geliştirildi .

Tanıtım

Pontryagin ikiliği, gerçek çizgi veya sonlu değişmeli gruplar üzerindeki fonksiyonlar hakkında bir dizi gözlemi birleşik bir bağlama yerleştirir:

• Gerçek çizgi üzerindeki uygun düzenli karmaşık değerli periyodik fonksiyonlar Fourier serilerine sahiptir ve bu fonksiyonlar onların Fourier serilerinden geri alınabilir;
• Gerçek hat üzerinde uygun şekilde düzenli karmaşık değerli fonksiyonlar, gerçek hat üzerinde de fonksiyonlar olan Fourier dönüşümlerine sahiptir ve tıpkı periyodik fonksiyonlarda olduğu gibi, bu fonksiyonlar onların Fourier dönüşümlerinden kurtarılabilir; ve
• Bir Kompleks değerli işlevler sonlu değişmeli grup sahip ayrık Fourier dönüşümü ile ilgili fonksiyonları, çift grup bir (kesintisiz-kanonik) izomorfik grubudur. Ayrıca, sonlu bir değişmeli grup üzerindeki herhangi bir fonksiyon, ayrık Fourier dönüşümünden geri kazanılabilir.

Tarafından tanıtılan teorisi, Lev Pontryagin ile ve kombine Haar tedbir getirdiği John von Neumann , André Weil ve diğerlerinin teorisi bağlıdır ikili grubun a yerel kompakt değişmeli grubunun.

Bir vektör uzayının ikili vektör uzayına benzer : sonlu boyutlu bir vektör uzayı V ve onun ikili vektör uzayı V* doğal olarak izomorfik değildir, ancak birinin endomorfizm cebiri (matris cebiri) endomorfizmin zıttı ile izomorfiktir. diğerinin cebiri: devrik yoluyla. Benzer şekilde, bir grup ve onun ikili grubu genel olarak izomorf değildir, ancak endomorfizm halkaları birbirine zıttır: . Daha kategorik olarak, bu sadece endomorfizm cebirlerinin bir eşbiçimliliği değil, kategorilerin zıt değişkenli denkliğidir - bkz. kategorik hususlar . ${\displaystyle {\text{End}}(V)\cong {{\text{End}}(V^{*})}^{\text{op}},}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\displaystyle {\text{End}}(G)\cong {\text{End}}({\widehat {G}})^{\text{op}}}$

Tanım

Bir topolojik grup , alttaki topolojik uzay yerel olarak kompakt ve Hausdorff ise, yerel olarak kompakt bir gruptur ; Topolojik grubudur değişmeli yatan grubu olduğu takdirde, değişmeli . Yerel olarak kompakt değişmeli grupların örnekleri arasında sonlu değişmeli gruplar, tam sayılar (her ikisi de ayrık topoloji için , aynı zamanda olağan metrik tarafından da indüklenir), gerçek sayılar, daire grubu T (her ikisi de olağan metrik topolojileriyle) ve ayrıca p -adic sayılar (her zamanki p -adic topolojileriyle birlikte).

Bir yerel kompakt değişmeli grup için , Pontryagin ikili grup sürekli bir grup homomorfizmalar gelen daire grubuna . Yani, ${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili G}$${\görüntüleme stili T}$

${\displaystyle {\widehat {G}}:=\operatöradı {Hom} (G,T).}$

Pontryagin ikilisi genellikle kompakt kümeler üzerinde tek biçimli yakınsama tarafından verilen topoloji ile donatılmıştır (yani, ' den ' ye kadar tüm sürekli fonksiyonların uzayında kompakt-açık topoloji tarafından indüklenen topoloji ). ${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili G}$${\görüntüleme stili T}$

Örneğin,

${\displaystyle {\widehat {\mathbb {Z}}}=T,\ {\widehat {\mathbb {R} }}=\mathbb {R} ,\ {\widehat {T}}=\mathbb {Z} .}$

Pontryagin dualite teoremi

Teorem :   Herhangi bir yerel olarak kompakt değişmeli grup ile onun ikili ikilisi arasında kanonik bir eşbiçimlilik vardır .${\displaystyle G\cong {\widehat {\widehat {G}}}}$${\görüntüleme stili G}$

Kanonik , doğal olarak tanımlanmış bir harita olduğu anlamına gelir  ; daha da önemlisi, harita olmalıdır Funktor içinde . Kanonik izomorfizm aşağıdaki gibi tanımlanır : ${\displaystyle \operatöradı {ev} _{G}\colon G\to {\widehat {\widehat {G}}}}$${\görüntüleme stili G}$${\displaystyle \operatöradı {ev} _{G}}$${\görüntüleme stili x\G'de}$

${\displaystyle \operatöradı {ev} _{G}(x)(\chi )=\chi (x)\in \mathbb {T} .\ {\text{ Yani, }}\ \operatöradı {ev} _ {G}(x):(\chi \mapsto \chi (x)).}$

Başka bir deyişle, her bir grup elemanı ikili üzerinde değerlendirme karakterine tanımlanır. Bu şiddetle benzerdir kanonik eşbiçimlilikle bir arasındaki sonlu boyutlu vektör uzayda ve çift çift , ve herhangi bir vektör uzayı söz etmek gerekiyor bir olduğunu değişmeli grup . Eğer sonlu bir değişmeli grup ise, o zaman bu izomorfizm kanonik değildir. Bu ifadeyi (genel olarak) kesin kılmak, ikilileştirmeyi bir işlev olarak ele almak ve özdeşlik işlevi ile ikilileştirme işlevinin doğal olarak eşdeğer olmadığını kanıtlamak için ikilileştirmeyi yalnızca gruplar üzerinde değil, aynı zamanda gruplar arasındaki haritalarda da düşünmeyi gerektirir . Ayrıca dualite teoremi, herhangi bir grup için (mutlaka sonlu olmak zorunda değil) dualizasyon fonktörünün tam bir fonksiyon olduğunu ima eder. ${\görüntüleme stili x}$${\ Displaystyle V\cong V^{**}}$${\görüntüleme stili V}$${\görüntüleme stili G}$${\ Displaystyle G\cong {\widehat {G}}}$

Pontryagin ikiliği ve Fourier dönüşümü

Haar ölçüsü

Bir yerel kompakt grup hakkında en dikkate değer gerçeklerden biri de esasen eşsiz doğal taşımasıdır tedbiri , Haar tedbiri biri sürekli yeterince düzenli alt kümelerinin "boyutunu" ölçmek için izin verir, . "Yeterince düzenli altküme" burada bir Borel kümesi anlamına gelir ; yani, kompakt kümeler tarafından üretilen σ-cebirinin bir elemanıdır . Daha kesin olarak, yerel olarak kompakt bir grup üzerindeki bir sağ Haar ölçüsü , bir elemanı ve bir Borel alt kümesi için μ( Ax ) = μ( A ) anlamında sağ değişmez olan Borel kümelerinde tanımlanan bir sayılabilir toplamsal ölçüdür μ ve ayrıca bazı düzenlilik koşullarını karşılar ( Haar ölçüsü ile ilgili makalede ayrıntılı olarak açıklanmıştır ). Pozitif ölçekleme faktörleri dışında, Haar ölçümü benzersizdir. ${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili x}$${\görüntüleme stili G}$${\görüntüleme stili A}$${\görüntüleme stili G}$${\görüntüleme stili G}$

Haar ölçüsü on, grup üzerinde tanımlanan ( karmaşık değerli) Borel fonksiyonları için integral kavramını tanımlamamızı sağlar . Özellikle, Haar ölçüsü μ ile ilişkili çeşitli L ^p boşlukları düşünülebilir . özellikle, ${\görüntüleme stili G}$

${\displaystyle {\mathcal {L}}_{\mu }^{p}(G)=\left\{(f:G\to \mathbb {C} )\ {\Big |}\ \int _{ G}|f(x)|^{p}\ d\mu (x)<\infty \sağ\}.}$

Herhangi iki Haar ölçüsü bir ölçekleme faktörüne eşit olduğundan, bu –uzay Haar ölçüsünün seçiminden bağımsızdır ve bu nedenle belki olarak yazılabilir . Bununla birlikte, bu uzaydaki –norm, Haar ölçüsünün seçimine bağlıdır, bu nedenle izometriler hakkında konuşmak isteniyorsa, kullanılan Haar ölçüsünün takip edilmesi önemlidir. ${\görüntüleme stili G}$${\görüntüleme stili L^{p}}$${\ Displaystyle L^{p}(G)}$${\görüntüleme stili L^{p}}$

L ¹ fonksiyonları için Fourier dönüşümü ve Fourier ters çevirme formülü

Yerel olarak kompakt bir değişmeli grubun ikili grubu, Fourier dönüşümünün soyut bir versiyonu için temel alan olarak kullanılır . Eğer , o zaman Fourier dönüşümü tarafından tanımlanan fonksiyondur .${\görüntüleme stili f\in L^{1}(G)}$${\ Displaystyle {\widehat {f}}}$${\ Displaystyle {\widehat {G}}}$

${\displaystyle {\widehat {f}}(\chi )=\int _{G}f(x){\overline {\chi (x)}}\ d\mu (x),}$

tamamlayıcı göre olduğu Haar ölçüsü ile . Bu da belirtilir . Fourier dönüşümünün Haar ölçüsünün seçimine bağlı olduğuna dikkat edin. Fourier bir dönüşümü göstermek için çok zor değildir işlevin bir sınırlı sürekli bir fonksiyonudur ki sonsuzda yok olur . ${\görüntüleme stili \mu }$${\görüntüleme stili G}$${\displaystyle ({\mathcal {F}}f)(\chi )}$${\görüntüleme stili L^{1}}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$

-Fonksiyonlar için Fourier Tersine Çevirme Formülü . ${\görüntüleme stili L^{1}}$Her Haar tedbir için üzerine orada eşsiz Haar ölçüsüdür üzerinde her şekilde ve biz var ${\görüntüleme stili \mu }$${\görüntüleme stili G}$${\görüntüleme stili \nu }$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili f\in L^{1}(G)}$${\displaystyle {\widehat {f}}\in L^{1}\left({\widehat {G}}\right)}$

${\displaystyle f(x)=\int _{\widehat {G}}{\widehat {f}}(\chi )\chi (x)\ d\nu (\chi )\qquad \mu {\text{ -neredeyse heryerde}}}$

Eğer sürekli ise bu özdeşlik herkes için geçerlidir .${\görüntüleme stili f}$${\görüntüleme stili x}$

Ters Fourier dönüşümü bir integre edilebilir fonksiyon ile verilmektedir ${\ Displaystyle {\widehat {G}}}$

${\displaystyle {\check {g}}(x)=\int _{\widehat {G}}g(\chi )\chi (x)\ d\nu (\chi ),}$

burada integral, ikili gruptaki Haar ölçüsüne göredir . Ölçer ile Fourier inversiyon formülü görülmektedir adlandırılan çift ölçü için ve ifade edilebilir . ${\görüntüleme stili \nu }$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili \nu }$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili \mu }$${\ Displaystyle {\widehat {\mu }}}$

Çeşitli Fourier dönüşümleri kendi etki bakımından sınıflandırılmış ve (not şöyle domain (grup ve ikili grup) dönüştürmek olabilir olduğu Çember grubu ): ${\displaystyle \mathbb {T} }$

dönüştürmek	Orijinal alan, ${\görüntüleme stili G}$	Alanı dönüştür, ${\displaystyle {\hat {G}}}$	Ölçüm, ${\görüntüleme stili \mu }$
Fourier dönüşümü	${\displaystyle \mathbb {R} }$	${\displaystyle \mathbb {R} }$	${\displaystyle {\text{Sabit}}\times {\text{Lebesgue ölçüsü}}}$
Fourier serisi	${\displaystyle \mathbb {T} }$	${\displaystyle \mathbb {Z} }$	${\displaystyle {\text{Sabit}}\times {\text{Lebesgue ölçüsü}}}$
Ayrık zamanlı Fourier dönüşümü (DTFT)	${\displaystyle \mathbb {Z} }$	${\displaystyle \mathbb {T} }$	${\displaystyle {\text{Sabit}}\times {\text{Sayma ölçüsü}}}$
Ayrık Fourier dönüşümü (DFT)	${\displaystyle \mathbb {Z} _{n}}$	${\displaystyle \mathbb {Z} _{n}}$	${\displaystyle {\text{Sabit}}\times {\text{Sayma ölçüsü}}}$

Bir örnek olarak, varsayalım Düşünmemiz, böylece olarak eşleştirme tarafından ise Öklid uzayında üzerinde Lebesgue ölçümü, biz sıradan elde Fourier dönüşümü üzerinde ve ikili tedbir Fourier inversiyon formülü için gerekli olan . Her iki tarafta da aynı ölçüye sahip bir Fourier inversiyon formülü elde etmek istiyorsak (yani, kendi dual uzayı olarak düşünebildiğimiz için , equal 'yi isteyebiliriz ), o zaman kullanmamız gerekir. ${\displaystyle G=\mathbb {R} ^{n}}$${\ Displaystyle {\widehat {G}}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} }.}$${\görüntüleme stili \mu }$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle {\widehat {\mu }}=(2\pi )^{-n}\mu }$${\displaystyle \mathbb {R} ^{n}}$${\ Displaystyle {\widehat {\mu }}}$${\görüntüleme stili \mu }$

${\displaystyle {\begin{hizalanmış}\mu &=(2\pi )^{-{\frac {n}{2}}}\times {\text{Lebesgue ölçüsü}}\\{\widehat {\mu }}&=(2\pi )^{-{\frac {n}{2}}}\times {\text{Lebesgue ölçüsü}}\end{hizalı}}}$

Ancak, ikili grubuyla özdeşleşme biçimimizi değiştirirsek , eşleştirmeyi kullanarak ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi i\mathbf {v} \cdot \mathbf {w} },}$

o zaman Lebesgue ölçüsü kendi ikili ölçüsüne eşittir . Bu kural , Öklid uzayında Fourier dönüşümleri veya ters Fourier dönüşümleri hesaplanırken çeşitli yerlerde görünen faktörlerin sayısını en aza indirir . (Aslında , integral işaretinin dışında bir ön faktör olarak değil , yalnızca üsle sınırlandırır .) İkili grubuyla nasıl özdeşleştirileceğinin seçiminin, "kendinden ikili işlev" teriminin anlamını etkilediğine dikkat edin. kendi Fourier dönüşümüne eşit bir fonksiyon : klasik eşleştirmeyi kullanarak fonksiyon kendi kendine çifttir. Ancak ön faktörü birlik olarak tutan eşleştirmeyi kullanmak, bunun yerine self-dual yapar . Fourier dönüşümü için bu ikinci tanım , bir evrişim cebiri kadar kullanışlı olan, çarpımsal kimliği evrişim kimliğine eşleme avantajına sahiptir . Grup cebiriyle ilgili sonraki bölüme bakın . Ayrıca bu form uzaylar üzerinde de zorunlu olarak izometriktir . Aşağıda Plancherel ve L ² Fourier inversiyon teoremlerine bakın.${\displaystyle \mathbb {R} ^{n}}$${\görüntüleme stili 2\pi }$${\görüntüleme stili 2\pi }$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} }}$${\displaystyle e^{-{\frac {1}{2}}x^{2}}}$${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi {i}{\mathbf {v} }\cdot {\mathbf {w} }}}$${\displaystyle e^{-\pi x^{2}}}$${\görüntüleme stili L^{1}}$${\ Displaystyle L^{2}}$

grup cebiri

Bir yerel kompakt değişmeli grubuna entegre edilebilir fonksiyonları alan bir olan cebri çarpma kıvrım olduğu,: iki entegre edilebilir fonksiyonları konvolüsyon ve olarak tanımlanmaktadır ${\görüntüleme stili G}$${\görüntüleme stili f}$${\görüntüleme stili g}$

${\displaystyle (f*g)(x)=\int _{G}f(xy)g(y)\ d\mu (y).}$

Teorem. Banach uzayı , evrişim altında birleştirici ve değişmeli bir cebirdir.${\görüntüleme stili L^{1}(G)}$

Bu cebir olarak adlandırılır Grup Cebir arasında . Tarafından Fubini-Tonelli teoremi , büklüm göre submultiplicative olan yapım norm bir Banach cebir . Banach cebiri , ancak ve ancak ayrı bir grup ise, yani özdeşlikte 1 ve başka yerde sıfır olan fonksiyonsa, çarpımsal bir özdeşlik unsuruna sahiptir . Bununla birlikte, genel olarak, yönlendirilmiş bir küme üzerinde indekslenen bir net (veya genelleştirilmiş dizi) olan yaklaşık bir özdeşliğe sahiptir, öyle ki:${\görüntüleme stili G}$${\görüntüleme stili L^{1}}$${\görüntüleme stili L^{1}(G)}$${\görüntüleme stili L^{1}(G)}$${\görüntüleme stili G}$${\displaystyle \{e_{i}\}_{i\in I}}$${\görüntüleme stili I}$${\displaystyle f*e_{i}\to f.}$

Fourier dönüşümü çarpma için evrişim alır, yani değişmeyen Banach cebirlerinin (norm ≤ 1'in) bir homomorfizmidir : ${\displaystyle L^{1}(G)\to C_{0}\left({\widehat {G}}\sağ)}$

${\displaystyle {\mathcal {F}}(f*g)(\chi )={\mathcal {F}}(f)(\chi )\cdot {\mathcal {F}}(g)(\chi ) .}$

Özellikle, üzerindeki her bir karaktere, aşağıdakiler tarafından tanımlanan grup cebirinde benzersiz bir çarpımsal doğrusal işlevselliğe karşılık gelir : ${\görüntüleme stili G}$

${\displaystyle f\mapsto {\widehat {f}}(\chi ).}$

Grup cebirinin önemli bir özelliği, bunların grup cebiri üzerindeki önemsiz olmayan (yani, aynı şekilde sıfır olmayan) çarpımsal doğrusal fonksiyoneller kümesini tüketmesidir; bkz. bölüm 34 ( Loomis 1953 ). Bu, Fourier dönüşümünün Gelfand dönüşümünün özel bir durumu olduğu anlamına gelir .

Plancherel ve L ² Fourier inversiyon teoremleri

Belirttiğimiz gibi, yerel olarak kompakt bir değişmeli grubun ikili grubu, kendi başına bir yerel olarak kompakt değişmeli gruptur ve bu nedenle bir Haar ölçüsüne veya daha kesin olarak, ölçekle ilgili bütün bir Haar ölçüleri ailesine sahiptir.

Teorem. Bir Haar ölçüsünü seç üzerinde ve izin üzerine ikili önlem yukarıda tanımlandığı gibi. Eğer o zaman kompakt desteğiyle süreklidir ve ${\görüntüleme stili \mu }$${\görüntüleme stili G}$${\görüntüleme stili \nu }$${\ Displaystyle {\widehat {G}}}$${\displaystyle f:G\to \mathbb {C} }$${\displaystyle {\widehat {f}}\in L^{2}\left({\widehat {G}}\right)}$

${\displaystyle \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat {G}}\left|{\widehat {f}}(\chi )\doğru|^{2}\ d\nu (\chi ).}$

Özellikle, Fourier dönüşümü bir bir kompakt destek karmaşık-değerli sürekli fonksiyonlardan izometri için ilgili -functions (kullanarak ilgili fonksiyonlar için u ile ilgili olarak -norm ve ilgili işlevler için cyclotron frekansının göre -norm ).${\ Displaystyle L^{2}}$${\görüntüleme stili G}$${\ Displaystyle L^{2}}$${\ Displaystyle {\widehat {G}}}$${\ Displaystyle L^{2}}$${\görüntüleme stili G}$${\ Displaystyle L^{2}}$${\ Displaystyle {\widehat {G}}}$

Kompakt desteğin kompleks değerli sürekli fonksiyonlar üzerindeki yana olan -dense, Fourier eşsiz uzantısı bir o uzaydan dönüşümü yoktur üniter operatör${\görüntüleme stili G}$${\ Displaystyle L^{2}}$

${\displaystyle {\mathcal {F}}:L_{\mu }^{2}(G)\to L_{\nu }^{2}\left({\widehat {G}}\right).}$

ve formülümüz var

${\displaystyle \forall f\in L^{2}(G):\quad \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat { G}}\sol|{\widehat {f}}(\chi )\sağ|^{2}\ d\nu (\chi ).}$

Kompakt olmayan yerel olarak kompakt gruplar için uzayın içermediğine dikkat edin , bu nedenle genel - fonksiyonların Fourier dönüşümü herhangi bir entegrasyon formülü (veya gerçekten herhangi bir açık formül) tarafından "verilmez". Fourier dönüşümünü tanımlamak için , kompakt destekli sürekli fonksiyonlar gibi yoğun bir alt uzaydan başlamak ve ardından izometriyi süreklilik yoluyla tüm uzaya genişletmek gibi bazı teknik hilelere başvurmak gerekir. Fourier dönüşümünün bu üniter uzantısı, kare integrallenebilir fonksiyonların uzayında Fourier dönüşümü ile kastettiğimiz şeydir. ${\görüntüleme stili G}$${\görüntüleme stili L^{1}(G)}$${\ Displaystyle L^{2}(G)}$${\ Displaystyle L^{2}}$${\görüntüleme stili G}$${\ Displaystyle L^{2}}$

İkili grup ayrıca kendi başına bir ters Fourier dönüşümüne sahiptir; Fourier dönüşümünün tersi (veya üniter olduğu için bitişik) olarak karakterize edilebilir . Bu, aşağıdaki Fourier inversiyon formülünün içeriğidir . ${\ Displaystyle L^{2}}$${\ Displaystyle L^{2}}$

Teorem. Kompakt desteğin sürekli fonksiyonlarıyla sınırlı Fourier dönüşümünün eki, ters Fourier dönüşümüdür.

${\displaystyle L_{\nu }^{2}\left({\widehat {G}}\right)\to L_{\mu }^{2}(G)}$

ikili ölçü nerede .${\görüntüleme stili \nu }$${\görüntüleme stili \mu }$

Durumda ikili grup tamsayılar grubuna doğal olarak izomorftur ve Fourier katsayılarının hesaplanması için uzmanlaşmış dönüşümü Fourier serilerinin periyodik fonksiyonların. ${\displaystyle G=\mathbb {T} }$${\ Displaystyle {\widehat {G}}}$${\displaystyle \mathbb {Z} }$

Eğer sonlu bir grup, biz kurtarmak ayrık Fourier dönüşümü . Bu davanın doğrudan kanıtlanmasının çok kolay olduğunu unutmayın. ${\görüntüleme stili G}$

Bohr sıkıştırma ve neredeyse periyodiklik

Pontryagin dualitesinin önemli bir uygulaması, kompakt değişmeli topolojik grupların aşağıdaki karakterizasyonudur:

teorem . Yerel olarak kompakt bir değişmeli grup , ancak ve ancak ikili grup ayrık ise kompakttır . Tersine, eğer ve sadece kompakt ise ayrıktır .${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$

Bu kompakt olan ima kesikli ya da farklı olmak anlamına gelir kompakt kompakt açık topoloji tanımının bir temel sonucudur ve Pontryagin ikilik gerek yoktur. Biri, konuşmaları kanıtlamak için Pontryagin ikiliğini kullanır. ${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\ Displaystyle {\widehat {G}}}$

Bohr kompaktifikasyonu herhangi topolojik grup için tanımlanır bakılmaksızın bakılmaksızın yerel kompakt veya değişmeli olduğunu. Kompakt değişmeli gruplar ve ayrık değişmeli gruplar arasında Pontryagin dualitesinden yapılan bir kullanım, keyfi bir değişmeli yerel kompakt topolojik grubun Bohr sıkıştırmasını karakterize etmektir . Bohr kompaktifikasyonu arasında olduğu burada, H grubu, bir yapıya sahiptir , ancak belirli bir ayrık topoloji . Dahil etme haritasından beri${\görüntüleme stili G}$${\görüntüleme stili G}$ ${\görüntüleme stili B(G)}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {H}}}$${\ Displaystyle {\widehat {G}}}$

${\ Displaystyle \ iota : H\to {\widehat {G}}}$

süreklidir ve bir homomorfizmadır, ikili morfizm

${\displaystyle G\sim {\widehat {\widehat {G}}}\to {\widehat {H}}}$

gerekli evrensel özelliği tatmin etmek için kolayca gösterilen kompakt bir gruba bir morfizmdir .

Ayrıca bkz . neredeyse periyodik fonksiyon .

kategorik düşünceler

Pontryagin ikiliği aynı zamanda işlevsel olarak da karlı bir şekilde düşünülebilir . Daha sonra gelende, LCA olduğu kategori yerel kompakt değişmeli gruplar ve sürekli grup homomorfizması. İkili grup yapı bir kontravaryant funktor olan LCA → LCA (anlamında temsil gösterilebilir funktorlar çember grubu tarafından) olarak özellikle, çift çift funktor olan bildirdiğinden . Pontryagin dualitesinin kategorik bir formülasyonu, LCA üzerindeki özdeşlik functor ile çift ​​dual functor arasındaki doğal dönüşümün bir izomorfizm olduğunu belirtir . Doğal bir dönüşüm kavramını çözerek, bu, haritaların herhangi bir yerel olarak kompakt değişmeli grup için izomorfizmler olduğu ve bu izomorfizmlerin . Bu izomorfizm benzerdir çift çift bir sonlu boyutlu vektör boşluklar (reel ve kompleks vektör alanları için özel bir durum). ${\ Displaystyle {\widehat {G}}}$${\displaystyle \mathbb {T} }$${\displaystyle {\widehat {G}}={\text{Hom}}(G,\mathbb {T} ).}$${\displaystyle G\to {\widehat {\widehat {G}}}}$${\displaystyle G\to \operatöradı {Hom} (\operatöradı {Hom} (G,T),T)}$${\görüntüleme stili G}$${\görüntüleme stili G}$

Bu formülasyonun dolaysız bir sonucu Pontryagin ikiliği bir başka sık rastlanan kategorik formülasyondur: Çift grubu funktoru bir olan kategorilerden denkliği gelen LCA için LCA ^op .

İkilik, ayrık grupların ve kompakt grupların alt kategorilerini değiştirir . Eğer bir olan halka ve bir sol olduğunu - modül , çift grup bir hak haline gelecektir Modül; bu şekilde ayrık sol modüllerin Pontryagin ikiliden kompakt sağ modüllere olacağını da görebiliriz . Halka içinde Endomorfizmlerin içinde LCA onun dualiteden ile değiştirilir zıt halka (diğer düzene çarpma değiştirme). Örneğin, eğer sonsuz bir döngüsel ayrık grup ise , bir daire grubudur: birincisi vardır , bu ikincisi için de geçerlidir. ${\görüntüleme stili R}$${\görüntüleme stili G}$${\görüntüleme stili R}$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili R}$${\görüntüleme stili R}$${\görüntüleme stili R}$${\görüntüleme stili {\metin{Bitiş}}(G)}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\displaystyle {\text{End}}(G)=\mathbb {Z} }$

genellemeler

Pontryagin ikiliği genellemeler iki ana yönde inşa edilir: değişmeli için topolojik gruplar değil yerel kompakt ve nonkomutatif topolojik gruplar için. Bu iki durumdaki teoriler çok farklı.

Değişmeli topolojik gruplar için ikilikler

Bir Hausdorff değişmeli topolojik grup olduğunda, kompakt-açık topolojiye sahip grup bir Hausdorff değişmeli topolojik gruptur ve onun çift-dual'ına doğal haritalama mantıklıdır. Bu eşleme bir eşbiçimlilik ise, Pontryagin ikiliğini (veya bunun bir dönüşlü grup veya bir yansıtıcı grup olduğu ) karşıladığı söylenir . Bu , yerel olarak kompakt olan durumun ötesinde bir dizi yönde genişletilmiştir . ${\görüntüleme stili G}$${\ Displaystyle {\widehat {G}}}$${\görüntüleme stili G}$${\ Displaystyle {\widehat {\widehat {G}}}}$${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili G}$

Özellikle, Samuel Kaplan, 1948 ve 1950'de, yerel kompakt (Hausdorff) değişmeli gruplarının keyfi çarpımlarının ve sayılabilir ters limitlerinin Pontryagin ikiliğini karşıladığını gösterdi. Yerel olarak kompakt kompakt olmayan uzayların sonsuz bir ürününün yerel olarak kompakt olmadığına dikkat edin.

Daha sonra, 1975'te Rangachari Venkataraman, diğer gerçeklerin yanı sıra, Pontryagin dualitesini sağlayan değişmeli bir topolojik grubun her açık alt grubunun Pontryagin dualitesini tatmin ettiğini gösterdi.

Daha yakın zamanlarda, Sergio Ardanza-Trevijano ve María Jesús Chasco, Kaplan'ın yukarıda bahsedilen sonuçlarını genişletti. Pontryagin dualitesini sağlayan değişmeli grup dizilerinin doğrudan ve ters limitlerinin, eğer gruplar metriklenebilir veya -uzaylar ise, ancak diziler tarafından bazı ekstra koşulların sağlanması şartıyla yerel olarak kompakt olması şartıyla, Pontryagin dualitesini de sağladığını gösterdiler. ${\görüntüleme stili k_{\omega }}$

Bununla birlikte, Pontryagin ikiliğini yerel olarak kompakt durumun ötesinde düşünmek istiyorsak değişen temel bir yön vardır. Elena Martín-Peinador 1995'te, eğer bir Hausdorff değişmeli topolojik grupsa, Pontryagin dualitesini ve doğal değerlendirme eşleşmesini tatmin ettiğini kanıtladı.${\görüntüleme stili G}$

${\displaystyle {\begin{cases}G\times {\widehat {G}}\to \mathbb {T} \\(x,\chi )\mapsto \chi (x)\end{cases}}}$

(birlikte) süreklidir, daha sonra yerel olarak kompakttır. Sonuç olarak, Pontryagin dualitesinin yerel olmayan tüm kompakt örnekleri, eşleştirmenin (ortak olarak) sürekli olmadığı gruplardır . ${\görüntüleme stili G}$${\displaystyle G\times {\widehat {G}}\to \mathbb {T}}$

Pontryagin dualitesini değişmeli topolojik grupların daha geniş sınıflarına genelleştirmenin bir başka yolu, dual gruba biraz farklı topoloji, yani tamamen sınırlı kümeler üzerinde tek tip yakınsama topolojisi kazandırmaktır . Bu varsayım altında özdeşliği sağlayan gruplara stereotip grupları denir . Bu sınıf da çok geniştir (ve yerel olarak kompakt değişmeli grupları içerir), ancak yansıtıcı gruplar sınıfından daha dardır. ${\ Displaystyle {\widehat {G}}}$${\displaystyle G\cong {\widehat {\widehat {G}}}}$

Topolojik vektör uzayları için Pontryagin dualitesi

1952'de Marianne F. Smith , topolojik gruplar olarak kabul edilen Banach uzayları ve dönüşlü uzayların (toplamsal grup işlemi ile) Pontryagin ikiliğini sağladığını fark etti . Daha sonra BS Brudovskiĭ, William C. Waterhouse ve K. Brauner, bu sonucun tüm yarı-tam namlulu alanların sınıfına (özellikle tüm Fréchet uzaylarına ) genişletilebileceğini gösterdi . 1990'larda Sergei Akbarov, klasik Pontryagin refleksivitesinden daha güçlü bir özelliği karşılayan topolojik vektör uzaylarının sınıfının bir tanımını verdi, yani özdeşlik.

${\ Displaystyle (X^{\star })^{\star }\cong X}$

nerede araçlar tüm lineer sürekli fonksiyonellerin uzay sahip tamamen sınırlandırılmış setlerinde tekdüze yakınlaşma topoloji içinde (ve araçlarına çift aynı anlamda). Bu sınıfın uzaylarına stereotip uzaylar denir ve karşılık gelen teori, değişmeli olmayan topolojik gruplar için Pontryagin dualitesinin genelleştirilmesi de dahil olmak üzere Fonksiyonel analiz ve Geometride bir dizi uygulama buldu. ${\görüntüleme stili X^{\yıldız }}$${\displaystyle f\colon X\to {\mathbb {C}}}$${\görüntüleme stili X}$${\görüntüleme stili (X^{\yıldız })^{\yıldız }}$${\görüntüleme stili X^{\yıldız }}$

Değişmeli olmayan topolojik gruplar için ikilikler

Değişmeli olmayan yerel kompakt gruplar için, klasik Pontryagin yapısı çeşitli nedenlerle çalışmayı durdurur, özellikle, çünkü karakterler her zaman noktalarını ayırmazlar ve indirgenemez temsilleri her zaman tek boyutlu değildir. Aynı zamanda, indirgenemez üniter temsiller kümesine çarpmanın nasıl dahil edileceği açık değildir ve bu kümenin ikili nesne rolü için iyi bir seçim olup olmadığı bile açık değildir . Dolayısıyla bu durumda dualite inşa etme problemi tamamen yeniden düşünmeyi gerektirir. ${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili G}$${\görüntüleme stili G}$

Bugüne kadar inşa edilen teoriler iki ana gruba ayrılır: İkili nesnenin kaynak nesneyle aynı doğaya sahip olduğu teoriler (Pontryagin ikiliğinin kendisinde olduğu gibi) ve kaynak nesne ile ikilinin birbirinden çok radikal bir şekilde farklılaştığı teoriler. onları bir sınıfın nesneleri olarak saymanın imkansız olduğunu.

İkinci tip teoriler tarihsel olarak ilkiydi: Pontryagin'in çalışmasından kısa bir süre sonra Tadao Tannaka (1938) ve Mark Kerin (1949), şimdi Tannaka-Krein ikiliği olarak bilinen keyfi kompakt gruplar için bir ikilik teorisi oluşturdu . Bu teoride bir grup için ikili nesne bir grup değil , onun temsillerinin bir kategorisidir . ${\görüntüleme stili G}$ ${\görüntüleme stili \Pi (G)}$

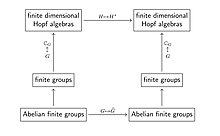
Birinci tip teoriler daha sonra ortaya çıktı ve onlar için anahtar örnek, sonlu gruplar için dualite teorisiydi. Bu teoride, sonlu gruplar kategorisi, grup cebirini (üzerinde ) sonlu boyutlu Hopf cebirleri kategorisine alma işlemiyle gömülüdür , böylece Pontryagin dualite functor , dual vektör uzayını (ki bu bir dualitedir) alma işlemine dönüşür. sonlu boyutlu Hopf cebirleri kategorisindeki functor). ${\displaystyle G\mapsto {\mathbb {C} }_{G}}$ ${\displaystyle {\mathbb {C} }_{G}}$${\displaystyle {\mathbb {C} }}$${\displaystyle G\mapsto {\widehat {G}}}$${\ Displaystyle H\mapsto H^{*}}$

1973'te Leonid I. Vainerman, George I. Kac, Michel Enock ve Jean-Marie Schwartz, tüm yerel kompakt gruplar için bu türden genel bir teori oluşturdu. 1980'lerden itibaren bu alandaki araştırmalar, kurulan teorilerin aktif olarak aktarılmaya başlandığı kuantum gruplarının keşfinden sonra yeniden başladı. Bu teoriler, C*-cebirleri veya Von Neumann cebirleri dilinde formüle edilmiştir ve varyantlarından biri, son zamanlarda yerel olarak kompakt kuantum grupları teorisidir .

Bununla birlikte, bu genel teorilerin dezavantajlarından biri, içlerinde grup kavramını genelleyen nesnelerin , alışılmış cebirsel anlamda Hopf cebirleri olmamasıdır . Bu eksiklik kavramına dayanarak inşa ikilik teorileri çerçevesinde (grupların bazılarını sınıflar için) düzeltilebilir zarf topolojik cebir.

Ayrıca bakınız

• Peter-Weyl teoremi
• Cartier ikiliği
• klişe alan

Notlar

Referanslar

• Dixmier, Jacques (1969). Les C*-algèbres et leurs Temsilcilikler . Gauthier-Villas. ISBN'si 978-2-87647-013-2.
• Enok, Michel; Schwartz, Jean-Marie (1992). Kac Cebirleri ve Yerel Kompakt Grupların Dualitesi . Alain Connes'ın önsözüyle. Adrian Ocneanu'nun bir postface'i ile. Berlin: Springer-Verlag. doi : 10.1007/978-3-662-02813-1 . ISBN'si 978-3-540-54745-7. MR  1215933 .
• Hewitt, Edwin; Ross, Kenneth A. (1963). Soyut Harmonik Analiz. Cilt I: Topolojik grupların yapısı. Entegrasyon teorisi, grup temsilleri . Die Grundlehren der matematikçi Wissenschaften. 115 . Berlin-Göttingen-Heidelberg: Springer-Verlag. ISBN'si 978-0-387-94190-5. MR  0156915 .
• Hewitt, Edwin; Ross, Kenneth A. (1970). Soyut Harmonik Analiz . 2 . ISBN'si 978-3-662-24595-8. MR  0262773 .
• Kirillov, Alexandre A. (1976) [1972]. Temsil teorisinin unsurları . Grundlehren der Mathematischen Wissenschaften. 220 . Berlin, New York: Springer-Verlag . ISBN'si 978-0-387-07476-4. MR  0412321 .
• Loomis, Lynn H. (1953). Soyut Harmonik Analize Giriş . D. van Nostrand Co. ISBN 978-0486481234.
• Morris, SA (1977). Pontryagin dualitesi ve yerel kompakt Abelian gruplarının yapısı . Cambridge Üniversitesi Yayınları . ISBN'si 978-0521215435.
• Onishchik, AL (1984). Pontrjagin ikiliği . Matematik Ansiklopedisi . 4 . s. 481-482. ISBN'si 978-1402006098.
• Reiter, Hans (1968). Klasik Harmonik Analiz ve Lokal Kompakt Gruplar . ISBN'si 978-0198511892.
• Rudin, Walter (1962). Gruplarda Fourier Analizi . D. van Nostrand Co. ISBN 978-0471523642.
• Timmermann, T. (2008). Kuantum Gruplarına ve Dualiteye Davet - Hopf Cebirlerinden Çarpımsal Üniterlere ve Ötesine . Matematikte EMS Ders Kitapları, Avrupa Matematik Derneği. ISBN'si 978-3-03719-043-2.
• Kustermans, J.; Vaes, S. (2000). "Yerel Kompakt Kuantum Grupları" . Annales Scientifiques de l'École Normale Supérieure . 33 (6): 837-934. doi : 10.1016/s0012-9593(00)01055-7 .
• Ardanza-Trevijano, Sergio; Chasco, Maria Jesús (2005). "Topolojik Değişkenli grupların sıralı sınırlarının Pontryagin ikiliği". Saf ve Uygulamalı Cebir Dergisi . 202 (1–3): 11–21. doi : 10.1016/j.jpaa.2005.02.006 . hdl : 10171/1586 . MR  2163398 .
• Chasco, Maria Jesús; Dikrancan, Dikran; Martín-Peinador, Elena (2012). "Değişmeli topolojik grupların refleksivitesi üzerine bir araştırma" . Topoloji ve Uygulamaları . 159 (9): 2290–2309. doi : 10.1016/j.topol.2012.04.012 . MR  2921819 .
• Kaplan, Samuel (1948). "Pontrjagin ikiliğinin uzantıları. Bölüm I: sonsuz ürünler". Duke Matematik Dergisi . 15 : 649-658. doi : 10.1215/S0012-7094-48-01557-9 . MR  0026999 .
• Kaplan, Samuel (1950). "Pontrjagin ikiliğinin uzantıları. Bölüm II: doğrudan ve ters sınırlar". Duke Matematik Dergisi . 17 : 419-435. doi : 10.1215/S0012-7094-50-01737-6 . MR  0049906 .
• Venkataraman, Rangachari (1975). "Pontryagin Dualitesinin Uzantıları". Matematiksel Zeitschrift . 143 (2): 105–112. doi : 10.1007/BF01187051 . S2CID  123627326 .
• Martin-Peinador, Elena (1995). "Bir yansıtılabilir kabul edilebilir topolojik grup yerel olarak kompakt olmalıdır". Amerikan Matematik Derneği Bildirileri . 123 (11): 3563-3566. doi : 10.2307/2161108 . hdl : 10338.dmlcz/127641 . JSTOR  2161108 .
• Smith, Marianne F. (1952). "Doğrusal uzaylarda Pontrjagin dualite teoremi". Matematik Annals . 56 (2): 248–253. doi : 10.2307/1969798 . JSTOR  1969798 . MR  0049479 .
• Brudovski, BS (1967). "Yerel dışbükey vektör uzaylarının k- ve c-yansımacılığı Üzerine". Litvanyalı Matematik Dergisi . 7 (1): 17–21.
• Waterhouse, William C. (1968). "Vektör uzaylarının ikili grupları" . Pasifik Matematik Dergisi . 26 (1): 193–196. doi : 10.2140/pjm.1968.26.193 .
• Brauner, Kalman (1973). "Fréchet uzaylarının Duals ve Banach-Dieudonné teoreminin bir genellemesi". Duke Matematik Dergisi . 40 (4): 845-855. doi : 10.1215/S0012-7094-73-04078-7 .
• Akbarov, SS (2003). "Topolojik vektör uzayları teorisinde ve topolojik cebirde Pontryagin ikiliği". Matematik Bilimleri Dergisi . 113 (2): 179–349. doi : 10.1023/A:1020929201133 . S2CID  115297067 .
• Akbarov, Sergei S.; Shavgulidze, Evgeniy T. (2003). "Pontryagin anlamında yansımalı uzayların iki sınıfı üzerinde" . Matematicheskii Sbornik . 194 (10): 3-26.
• Akbarov, Sergei S. (2009). "Kimliğin cebirsel bağlantılı bileşeni ile Stein grupları için üstel tip ve dualitenin holomorfik fonksiyonları". Matematik Bilimleri Dergisi . 162 (4): 459–586. arXiv : 0806.3205 . doi : 10.1007/s10958-009-9646-1 . S2CID  115153766 .
• Akbarov, Sergei S. (2017). "Topolojik cebirlerin sürekli ve düzgün zarfları. Bölüm 1". Matematik Bilimleri Dergisi . 227 (5): 531–668. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3599-6 . MR  3790317 . S2CID  126018582 .
• Akbarov, Sergei S. (2017). "Topolojik cebirlerin sürekli ve düzgün zarfları. Bölüm 2". Matematik Bilimleri Dergisi . 227 (6): 669-789. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3600-4 . MR  3796205 . S2CID  128246373 .