polilogaritma - Polylogarithm

Gelen matematik , polylogarithm (aynı zamanda Jonquière fonksiyonu Alfred Jonquière için), a, özel fonksiyon Li _s ( z emri) lar ve bağımsız değişken z . Yalnızca s'nin özel değerleri için , polilogaritma , doğal logaritma veya rasyonel bir işlev gibi temel bir işleve indirgenir . Olarak kuantum istatistikleri , polylogarithm fonksiyonu kapalı form olarak görünür integrallerin arasında Fermi Dirac dağılımı ve Bose-Einstein dağılımı ve aynı zamanda bilinen Fermi Dirac integrali veya Bose-Einstein integrali . Olarak kuantum elektrodinamik bir konumda bir polylogarithms tam sayı için daha yüksek dereceden ile temsil edilen işlemler hesaplanmasında ortaya Feynmann diyagramları .

Polylogaritma işlevi, Hurwitz zeta işlevine eşdeğerdir - her iki işlev de diğeri cinsinden ifade edilebilir - ve her iki işlev de Lerch aşkının özel durumlarıdır . Polilogaritmalar, polilogaritmik fonksiyonlarla veya aynı gösterime sahip, ancak tek değişkenli ofset logaritmik integral ile karıştırılmamalıdır .

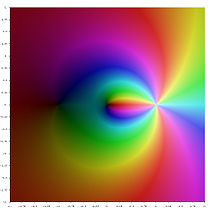
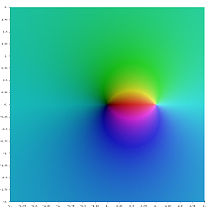
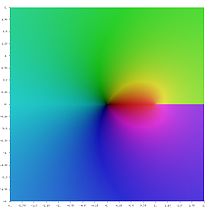
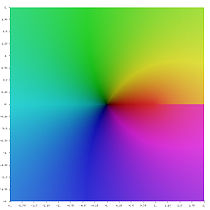
• Karmaşık düzlemde farklı polilogaritma fonksiyonları
• 

  Li _-3 ( z )

• 

  Li _-2 ( z )

• 

  Li _-1 ( z )

• 

  Li ₀ ( z )

• 

  Li ₁ ( z )

• 

  Li ₂ ( z )

• 

  Li ₃ ( z )

Polylogarithm fonksiyonu ile tanımlanır güç seri olarak z da olduğu, Dirichlet serisi içinde s :

${\displaystyle \operatöradı {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}=z+{z^{2 } \2^{s}}+{z^{3} \3^{s}}+\cdots }$

Bu tanım, rastgele karmaşık sıra s için ve | ile tüm karmaşık z argümanları için geçerlidir. z | < 1; uzatılabilir | z | ≥ 1 analitik devam süreci ile . (Burada n ^s paydası exp(s ln(n) olarak anlaşılır.) Özel durum s = 1, sıradan doğal logaritmayı , Li ₁ ( z ) = −ln(1− z ) içerirken, özel durumlar s = 2 ve s = 3 sırasıyla dilogaritma ( Spence'nin işlevi olarak da adlandırılır) ve trilogaritma olarak adlandırılır.Fonksiyonun adı , kendisinin tekrarlanan integrali olarak da tanımlanabilmesi gerçeğinden gelir :

${\displaystyle \operatöradı {Li} _{s+1}(z)=\int _{0}^{z}{\frac {\operatöradı {Li} _{s}(t)}{t}}dt }$

bu nedenle dilogaritma, logaritmayı içeren bir fonksiyonun integralidir, vb. Nonpositive tamsayı siparişleri için s , polylogarithm bir olan rasyonel fonksiyon .

Özellikler

Polilogaritma sırasının bir tamsayı olması durumunda, (veya negatif olduğunda) ile temsil edilecektir . Tanımlamak için genellikle daha uygun nerede olduğunu asıl şube ait kompleks logaritma böylece Ayrıca, tüm üs alma tek değerli olduğu kabul edilecektir:${\görüntüleme stili s}$${\görüntüleme stili n}$${\görüntüleme stili -n}$${\görüntüleme stili \mu =\ln(z)}$${\görüntüleme stili \ln(z)}$ ${\displaystyle \operatöradı {Ln} (z)}$${\displaystyle -\pi <\operatöradı {Im} (\mu )\leq \pi .}$${\displaystyle z^{s}=\exp(s\ln(z))).}$

Sipariş bağlı olarak , polylogarithm çok değerli olabilir. Ana dal içinde alınır verilecek olan yukarıdaki dizi tanım itibariyle ve bir kesim yapılır pozitif reel eksene dışında sürekli olarak alınır için eksen alt yarısı düzlemine yerleştirilir öyle ki . açısından , bu tutar . Polylogaritmanın bağımlı olarak süreksizliği bazen kafa karıştırıcı olabilir. ${\görüntüleme stili s}$${\displaystyle \operatöradı {Li} _{s}(z)}$${\görüntüleme stili |z|<1}$${\görüntüleme stili z=1}$${\görüntüleme stili \infty }$${\görüntüleme stili z}$${\görüntüleme stili \mu }$${\displaystyle -\pi <\operatöradı {arg} (-\mu )\leq \pi }$${\görüntüleme stili \mu }$

Gerçek argüman için , gerçek düzenin polylogarithm eğer gerçek , ve onun sanal kısmı (olan Ahşap 1992 , § 3): ${\görüntüleme stili z}$${\görüntüleme stili s}$${\görüntüleme stili z<1}$${\displaystyle z\geq 1}$

${\displaystyle \operatöradı {Im} \sol(\operatöradı {Li} _{s}(z)\sağ)=-{{\pi \mu ^{s-1}} \over {\Gama (lar)} }.}$

Kesitten geçersek , eğer ε sonsuz derecede küçük bir pozitif gerçek sayı ise, o zaman:

${\displaystyle \operatöradı {Im} \left(\operatöradı {Li} _{s}(z+i\epsilon )\sağ)={{\pi \mu ^{s-1}} \over {\Gama ( s)}}.}$

Her ikisi de Li _s'nin ( e ^µ ) µ = 0 civarında seri açılımından ( aşağıya bakınız ) çıkarılabilir .

Polilogaritma türevleri, tanımlayıcı güç serilerinden gelir:

${\displaystyle z{\frac {\partial\operatöradı {Li} _{s}(z)}{\partial z}}=\operatöradı {Li} _{s-1}(z)}$

${\displaystyle {\frac {\partial\operatöradı {Li} _{s}(e^{\mu })}{\partial\mu }}=\operatöradı {Li} _{s-1}(e^{ \mu }).}$

Kare ilişkisi seri tanımından görülür ve çoğaltma formülüyle ilgilidir (ayrıca bkz. Clunie (1954) , Schrödinger (1952) ):

${\displaystyle \operatöradı {Li} _{s}(-z)+\operatöradı {Li} _{s}(z)=2^{1-s}\operatöradı {Li} _{s}(z^{ 2}).}$

Kummer'in işlevi , çok benzer bir çoğaltma formülüne uyar. Bu, herhangi bir pozitif tamsayı p için çarpma formülünün özel bir durumudur :

${\displaystyle \sum _{m=0}^{p-1}\operatöradı {Li} _{s}(ze^{2\pi im/p})=p^{1-s}\operatöradı {Li } _{s}(z^{p}),}$

bu, polilogaritmanın seri tanımı ve üstel terimlerin ortogonalliği kullanılarak kanıtlanabilir (bkz. örneğin ayrık Fourier dönüşümü ).

Diğer bir önemli özellik olan ters çevirme formülü, Hurwitz zeta fonksiyonunu veya Bernoulli polinomlarını içerir ve aşağıdaki diğer fonksiyonlarla ilişkisi altında bulunur.

özel değerler

Özel durumlar için, polilogaritma diğer fonksiyonlar cinsinden ifade edilebilir ( aşağıya bakınız ). Polilogaritma için özel değerler, bu nedenle, bu diğer fonksiyonların özel değerleri olarak da bulunabilir.

1. Polilogaritma düzeninin tamsayı değerleri için, z ·∂/∂ z'nin Li _1'e ( z ) tekrar tekrar uygulanmasıyla aşağıdaki açık ifadeler elde edilir :

   ${\displaystyle \operatöradı {Li} _{1}(z)=-\ln(1-z)}$

   ${\displaystyle \operatöradı {Li} _{0}(z)={z \over 1-z}}$

   ${\displaystyle \operatöradı {Li} _{-1}(z)={z \over (1-z)^{2}}}$

   ${\displaystyle \operatöradı {Li} _{-2}(z)={z(1+z) \over (1-z)^{3}}}$

   ${\displaystyle \operatöradı {Li} _{-3}(z)={z(1+4z+z^{2}) \over (1-z)^{4}}}$

   ${\displaystyle \operatöradı {Li} _{-4}(z)={z(1+z)(1+10z+z^{2}) \over (1-z)^{5}}.}$

   Bu duruma göre polylogarithm polinomların bir oranda azaltır z ve bu nedenle, bir rasyonel fonksiyonu arasında z tüm pozitif olmayan tam sayı siparişleri için,. Genel durum sonlu bir toplam olarak ifade edilebilir:

   ${\displaystyle \operatöradı {Li} _{-n}(z)=\left(z{\partial \over\partial z}\right)^{n}{z \over {1-z}}=\sum _{k=0}^{n}k!S(n+1,k+1)\left({z \over {1-z}}\sağ)^{k+1}\qquad (n=0 ,1,2,\ldotlar ),}$

   burada S ( n , k ) ikinci türün Stirling sayılarıdır . Negatif tamsayı düzenleri için geçerli eşdeğer formüller şunlardır ( Wood 1992 , § 6):

   ${\displaystyle \operatöradı {Li} _{-n}(z)=(-1)^{n+1}\sum _{k=0}^{n}k!S(n+1,k+1 )\left({{-1} \over {1-z}}\sağ)^{k+1}\qquad (n=1,2,3,\ldots ),}$

   ve:

   ${\displaystyle \operatöradı {Li} _{-n}(z)={1 \over (1-z)^{n+1}}\sum _{k=0}^{n-1}\left\ açı {n \atop k}\sağ\rangle z^{nk}\qquad (n=1,2,3,\ldots ),}$

   nerede olduğu Euler sayıları . Li _{- n} ( z )'nin tüm kökleri farklı ve gerçektir; z = 0'ı içerirler , geri kalan ise negatiftir ve logaritmik bir ölçekte z = -1 etrafında ortalanır . As n büyük olur, bu rasyonel ifadelerin sayısal değerlendirme giderek iptal dan (uğrar Wood 1992 , § 6); Ancak tam doğruluk , Hurwitz zeta fonksiyonu ile genel ilişki yoluyla Li _{- n} ( z ) hesaplanarak elde edilebilir ( aşağıya bakınız ). ${\displaystyle \scriptstyle \sol\langle {n \atop k}\sağ\rangle }$
2. z bağımsız değişkeninin yarı tamsayı değerleri için bazı özel ifadeler şunlardır:

   ${\displaystyle \operatöradı {Li} _{1}({\tfrac {1}{2}})=\ln 2}$

   ${\displaystyle \operatöradı {Li} _{2}({\tfrac {1}{2}})={\tfrac {1}{12}}\pi ^{2}-{\tfrac {1}{2 }}(\ln 2)^{2}}$

   ${\displaystyle \operatöradı {Li} _{3}({\tfrac {1}{2}})={\tfrac {1}{6}}(\ln 2)^{3}-{\tfrac {1 }{12}}\pi ^{2}\ln 2+{\tfrac {7}{8}}\zeta (3),}$

   burada ζ , Riemann zeta fonksiyonudur . Daha yüksek tamsayı mertebeleri için bu türden hiçbir formül bilinmemektedir ( Lewin 1991 , s. 2), ancak örneğin şöyle bir formül vardır ( Borwein, Borwein & Girgensohn 1995 ):

   ${\displaystyle \operatöradı {Li} _{4}({\tfrac {1}{2}})={\tfrac {1}{360}}\pi ^{4}-{\tfrac {1}{24 }}(\ln 2)^{4}+{\tfrac {1}{24}}\pi ^{2}(\ln 2)^{2}-{\tfrac {1}{2}}\zeta ({\bar {3}},{\bar {1}}),}$

   alternatif çift toplamı içeren

   ${\displaystyle \zeta ({\bar {3}},{\bar {1}})=\sum _{m>n>0}(-1)^{m+n}m^{-3}n ^{-1}.}$

   Genelde n ≥ 2 tamsayı düzeni vardır ( Broadhurst 1996 , s. 9):

   ${\displaystyle \operatöradı {Li} _{n}({\tfrac {1}{2}})=-\zeta ({\bar {1}},{\bar {1}},\left\{1 \sağ\}^{n-2}),}$

   burada ζ ( s ₁ , …, s _k ) çoklu zeta işlevidir ; Örneğin:

   ${\displaystyle \operatöradı {Li} _{5}({\tfrac {1}{2}})=-\zeta ({\bar {1}},{\bar {1}},1,1,1 ).}$

3. Seri tanımının doğrudan bir sonucu olarak, birliğin p th karmaşık köklerindeki polilogaritma değerleri Fourier toplamı ile verilir :

   ${\displaystyle \operatöradı {Li} _{s}(e^{2\pi im/p})=p^{-s}\sum _{k=1}^{p}e^{2\pi imk /p}\zeta (s,{\tfrac {k}{p}})\qquad (m=1,2,\dots ,p-1),}$

   burada ζ olan Hurwitz zeta fonksiyonu . Li _s (1)'in sonlu olduğu Re( s ) > 1 için, bağıntı m = 0 veya m = p ile de geçerlidir . Bu formül, aşağıdaki diğer fonksiyonlarla ilişkisi altında listelenen Hurwitz zeta fonksiyonu ile daha genel bir ilişkinin ima ettiği kadar basit olmasa da , s'nin negatif olmayan tamsayı değerlerine de uygulama avantajına sahiptir . Her zamanki gibi, herhangi bir m = 1, …, p için ζ( s , ^m ⁄ _p ) ifadesini Li _s (exp(2 πi ^k ⁄ _p )) üzerinden k = 1, … , s .

Diğer işlevlerle ilişki

• İçin z = 1 polylogarithm azaltır Riemann zeta fonksiyonu

  ${\displaystyle \operatöradı {Li} _{s}(1)=\zeta (s)\qquad (\operatöradı {Re} (s)>1).}$

• Polilogaritma, Dirichlet eta işlevi ve Dirichlet beta işleviyle ilgilidir :

  ${\displaystyle \operatöradı {Li} _{s}(-1)=-\eta(lar),}$

  burada η ( s ) Dirichlet eta fonksiyonudur. Saf hayali argümanlar için elimizde:

  ${\displaystyle \operatöradı {Li} _{s}(\pm i)=-2^{-s}\eta(s)\pm i\beta(s),}$

  burada β ( s ) Dirichlet beta işlevidir.

• Polilogaritma, tam Fermi-Dirac integrali ile şu şekilde ilişkilidir :

  ${\displaystyle F_{s}(\mu )=-\operatöradı {Li} _{s+1}(-e^{\mu }).}$

• Polilogaritma, eksik polilogaritma fonksiyonunun özel bir halidir.

  ${\displaystyle \operatöradı {Li} _{s}(z)=\operatöradı {Li} _{s}(0,z).}$

• Polylogaritma, Lerch aşkının özel bir durumudur ( Erdélyi ve diğerleri 1981 , § 1.11-14)

  ${\displaystyle \operatöradı {Li} _{s}(z)=z\Phi (z,s,1).}$

• Polilogaritma, Hurwitz zeta işleviyle şu şekilde ilişkilidir :

  ${\displaystyle \operatöradı {Li} _{s}(z)={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}\zeta \left(1-s,{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\sağ)+i^{s-1}~\zeta \left (1-s,{\frac {1}{2}}-{\ln(-z) \over {2\pi i}}\sağ)\sağ],}$

  bu ilişki, bununla birlikte, bir pozitif tam sayı de geçerli olmak s göre kutup arasında gama fonksiyonu y (1- s ), ve en s iki zeta fonksiyonu bir kutup tarafından = 0; Bu formülün bir türevi aşağıdaki seri gösterimleri altında verilmiştir. Hurwitz zeta fonksiyonu için bir fonksiyonel denklemden biraz yardım alarak, polilogaritma sonuç olarak bu fonksiyonla da ilişkilidir ( Jonquière 1889 ):

  ${\displaystyle i^{-s}\operatöradı {Li} _{s}(e^{2\pi ix})+i^{s}\operatöradı {Li} _{s}(e^{-2\ pi ix})={(2\pi )^{s} \over \Gamma (s)}\zeta (1-s,x),}$

  bu ilişki Im( x ) ≥ 0 ise 0 ≤ Re( x ) < 1 için ve Im( x ) < 0 ise 0 < Re( x ) ≤ 1 için geçerlidir. Eşdeğer olarak, tüm s kompleksleri ve z ∉ ∉ ] 0;1], ters çevirme formülü okur

  ${\displaystyle \operatöradı {Li} _{s}(z)+(-1)^{s}\operatöradı {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right), }$

  ve tüm karmaşık s için ve karmaşık z için ∉ ]1;∞[

  ${\displaystyle \operatöradı {Li} _{s}(z)+(-1)^{s}\operatöradı {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right ).}$

  İçin z ∉] 0 (- ∞ [bir ln sahiptir z ) = -ln (- ¹ / _z ), ve her iki ifade kabul eder. Bu ilişkiler, polilogaritmanın yakınsama çemberinin ötesinde analitik devamını sağlar | z | = Tanımlayıcı güç serisinin 1'i. ( Jonquière (1889 , eq. 5) ve Erdélyi ve arkadaşlarının (1981 , § 1.11-16) karşılık gelen denklemi , polilogaritmanın ve logaritmanın ana dallarının aynı anda kullanıldığı varsayılırsa doğru değildir.) Sonraki bölüme bakınız. s bir tamsayı olduğunda basitleştirilmiş bir formül için öğe .

• Pozitif tamsayı polilogaritma mertebeleri s için , Hurwitz zeta fonksiyonu ζ(1− s , x ) Bernoulli polinomlarına , ζ(1− n , x ) = −B _n ( x ) / n ve Jonquière'in n = 1 için ters çevirme formülüne indirgenir , 2, 3, … şöyle olur:

  ${\displaystyle \operatöradı {Li} _{n}(e^{2\pi ix})+(-1)^{n}\operatöradı {Li} _{n}(e^{-2\pi ix} )=-{(2\pi i)^{n} \over n!}B_{n}(x),}$

  burada yine 0 ≤ Re( x ) < 1 eğer Im( x ) ≥ 0 ise ve 0 < Re( x ) ≤ 1 ise Im( x ) < 0. Çoklogaritma argümanının birim çembere kısıtlanması üzerine, Im( x ) = 0, 2 Re (Li bu formül basitleştirir sol taraftaki _n ( e ^{2 πix} )) ise n bile, ve 2'ye i Im (Li _{, n} ( e ^{2 πix} )) ise n garip. Negatif tamsayı mertebeleri için ise, Γ( s )' nin diverjansı, tüm z için şu anlama gelir ( Erdélyi et al. 1981 , § 1.11-17):

  ${\displaystyle \operatöradı {Li} _{-n}(z)+(-1)^{n}\operatöradı {Li} _{-n}(1/z)=0\qquad (n=1,2 ,3,\ldotlar ).}$

  Daha genel olarak, n = 0, ±1, ±2, ±3, … için vardır:

  ${\displaystyle \operatöradı {Li} _{n}(z)+(-1)^{n}\operatöradı {Li} _{n}(1/z)=-{\frac {(2\pi i) ^{n}}{n!}}B_{n}\left({\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\sağ)\qquad ( z\değil ]0;1]),}$

  ${\displaystyle \operatöradı {Li} _{n}(z)+(-1)^{n}\operatöradı {Li} _{n}(1/z)=-{\frac {(2\pi i) ^{n}}{n!}}B_{n}\left({\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\sağ)\ qquad (z\not \in ~]1;\infty [),}$

  burada her iki ifade de z ∉ ]0;∞[ için uyumludur. ( Jonquière (1889 , eq. 1) ve Erdélyi ve arkadaşlarının (1981 , § 1.11-18) karşılık gelen denklemi yine doğru değildir.)

• Saf hayali μ ile polilogaritma , Clausen fonksiyonları Ci _s (θ) ve Si _s (θ) ve bunun tersi olarak ifade edilebilir ( Lewin 1958 , Bölüm VII § 1.4; Abramowitz & Stegun 1972 , § 27.8):

  ${\displaystyle \operatöradı {Li} _{s}(e^{\pm i\theta})=Ci_{s}(\theta )\pm iSi_{s}(\theta ).}$

• Ters tanjant entegre Ti _s ( Z ) ( Lewin 1958 ., Bölüm VII § 1.2) polylogarithms cinsinden ifade edilebilir:

  ${\displaystyle \operatöradı {Ti} _{s}(z)={1 \over 2i}\left[\operatöradı {Li} _{s}(iz)-\operatöradı {Li} _{s}(-iz )\sağ].}$

  İlişki özellikle şu anlama gelir:

  ${\displaystyle \operatöradı {Ti} _{0}(z)={z \over 1+z^{2}},\quad \operatöradı {Ti} _{1}(z)=\arctan z,\quad \operatöradı {Ti} _{2}(z)=\int _{0}^{z}{\arctan t \over t}dt,\quad \ldots ~\quad \operatöradı {Ti} _{n+1 }(z)=\int _{0}^{z}{\frac {\operatör adı {Ti} _{n}(t)}{t}}dt,}$

  hangi işlev adını açıklar.

• Legendre chi fonksiyonu , x, _s ( Z ) ( Lewin 1958 , Bölüm VII § 1.1;. Boersma ve 1992 Dempsey ) polylogarithms cinsinden ifade edilebilir:

  ${\displaystyle \chi _{s}(z)={\tfrac {1}{2}}\left[\operatöradı {Li} _{s}(z)-\operatöradı {Li} _{s}(- z)\sağ].}$

• Tamsayı mertebesinin polilogaritması genelleştirilmiş bir hipergeometrik fonksiyon olarak ifade edilebilir :

  ${\displaystyle \operatöradı {Li} _{n}(z)=z_{n+1}F_{n}(1,1,\dots ,1;2,2,\dots ,2;z)\qquad ( n=0,1,2,\ldots ),}$

  ${\displaystyle \operatöradı {Li} _{-n}(z)=z_{n}F_{n-1}(2,2,\dots ,2;1,1,\dots ,1;z)\qquad (n=1,2,3,\ldots )~.}$

Açısından eksik zeta fonksiyonu ya da " Debye fonksiyonları " ( Abramowitz ve Stegun 1972 , § 27.1):

${\displaystyle Z_{n}(z)={1 \over (n-1)!}\int _{z}^{\infty }{t^{n-1} \over e^{t}-1 }dt\qquad (n=1,2,3,\ldots ),}$

pozitif tamsayı n için Li _n ( z ) polilogaritma sonlu toplam olarak ifade edilebilir ( Wood 1992 , § 16):

${\displaystyle \operatöradı {Li} _{n}(e^{\mu })=\sum _{k=0}^{n-1}Z_{nk}(-\mu ){\mu ^{k } \k üzerinde!}\qquad (n=1,2,3,\ldots ).}$

Oldukça benzer bir ifade, "Debye işlevleri" Z _n ( z ) ile polilogaritma ile ilgilidir:

${\displaystyle Z_{n}(z)=\sum _{k=0}^{n-1}\operatöradı {Li} _{nk}(e^{-z}){z^{k} \over k!}\qquad (n=1,2,3,\ldots ).}$

• Kullanılması Lambert serisi ise, olup Ürdün'ün totient işlevi daha sonra,${\displaystyle J_{s}(n)}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {z^{n}J_{-s}(n)}{1-z^{n}}}=\operatöradı {Li} _{s}(z).}$

integral temsiller

Aşağıdaki integral gösterimlerden herhangi biri, polilogaritmanın yakınsama çemberinin ötesinde analitik devamını sağlar | z | = Tanımlayıcı güç serisinin 1'i.

1. Polilogaritma, Bose-Einstein dağılımının integrali cinsinden ifade edilebilir :

   ${\displaystyle \operatorname {Li} _{s}(z)={1 \over \Gamma (s)}\int _{0}^{\infty }{t^{s-1} \over e^{ t}/z-1}dt.}$

   Bu, Re( s ) > 0 ve z gerçel ve ≥ 1 hariç tüm z için yakınsar. Bu bağlamda polilogaritma bazen Bose integrali olarak adlandırılır, ancak daha yaygın olarak Bose–Einstein integrali olarak adlandırılır . Benzer şekilde, polilogaritma, Fermi-Dirac dağılımının integrali cinsinden ifade edilebilir :

   ${\displaystyle -\operatöradı {Li} _{s}(-z)={\frac {1}{\Gamma(s)}}\int _{0}^{\infty }{t^{s-1 } \over e^{t}/z+1}dt.}$

   Bu, Re( s ) > 0 ve z gerçel ve ≤ -1 hariç tüm z için yakınsar . Bu bağlamda polilogaritma bazen bir Fermi integrali veya bir Fermi–Dirac integrali olarak adlandırılır ( GSL 2010 ). Bu temsiller , integralin z'ye göre Taylor açılımı ve terimsel entegrasyon ile kolayca doğrulanır . Dingle'ın makaleleri, her iki tür integralin ayrıntılı araştırmalarını içerir. Polilogaritma, Maxwell-Boltzmann dağılımının integrali ile de ilgilidir :

   ${\displaystyle \lim _{z\to 0}{\frac {\operatör adı {Li} _{s}(z)}{z}}={1 \over \Gamma(lar)}\int _{0} ^{\infty }{t^{s-1}e^{-t}}dt=1.}$

   Bu aynı zamanda polilogaritmanın orijin civarında asimptotik davranışını verir .
2. Tamamlayıcı bir integral gösterimi Re( s ) < 0 için ve z gerçel ve ≥ 0 hariç tüm z için geçerlidir :

   ${\displaystyle \operatöradı {Li} _{s}(z)=\int _{0}^{\infty }{t^{-s}\sin[s\pi /2-t\ln(-z) ] \üstü \sinh(\pi t)}dt.}$

   Bu integral, polilogaritma ile Hurwitz zeta fonksiyonu arasındaki genel ilişkiden ( yukarıya bakınız ) ve ikincisinin bilinen bir integral temsilinden kaynaklanmaktadır.
3. Polylogarithm oldukça genel bir ile temsil edilebilir Hankel kontur integrali ( Whittaker ve Watson 1927 negatif siparişleri Bose-Einstein temsil uzanır, § 12.22, § 13.13), s . İntegradın t = μ kutbu negatif olmayan reel eksen üzerinde olmadığı ve s ≠ 1, 2, 3, … olduğu sürece , elimizde:

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=-{{\Gamma (1-s)} \over {2\pi i}}\oint _{H}{{( -t)^{s-1}} \over {e^{t-\mu }-1}}dt}$

   burada H , Hankel çevresini temsil eder. İntegrant, gerçek eksen boyunca sıfırdan sonsuza kadar bir kesime sahiptir ve eksen t'nin alt yarı düzlemine aittir . Entegrasyon üst yarı düzlemde +∞'de başlar (Im( t ) > 0), orijini t = µ + 2 kπi kutuplarından herhangi birini çevrelemeden çevreler ve alt yarı düzlemde + ∞'de sona erer (Im( t ) ) < 0). µ'nin gerçek ve negatif olmadığı durumda , ekteki t = µ kutbunun katkısını basitçe çıkarabiliriz :

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=-{{\Gamma (1-s)} \over {2\pi i}}\oint _{H}{{( -t)^{s-1}} \over {e^{t-\mu }}-1}dt-2\pi iR}$

   burada R , direğin kalıntısıdır :

   ${\displaystyle R={i \over 2\pi }\Gamma (1-s)(-\mu )^{s-1}.}$

4. Tüm Abel-Plana formül polylogarithm'e tanımlayan dizi uygulanır, bir Hermite kompleks için geçerlidir integral gösterimi sonuçları -tipi z bütün kompleks için s :

   ${\displaystyle \operatöradı {Li} _{s}(z)={\tfrac {1}{2}}z+{\Gamma (1-s,-\ln z) \over (-\ln z)^{ 1-s}}+2z\int _{0}^{\infty }{\frac {\sin(s\arctan tt\ln z)}{(1+t^{2})^{s/2} (e^{2\pi t}-1)}}dt}$

   burada Γ üst tamamlanmamış gama işlevidir . Bu ifadedeki ln( z ) öğesinin tümü (bir kısmı hariç) −ln( ¹ ⁄ _z ) ile değiştirilebilir. Tüm karmaşık s için de geçerli olan ilgili bir temsil ,

   ${\displaystyle \operatöradı {Li} _{s}(z)={\tfrac {1}{2}}z+z\int _{0}^{\infty }{\frac {\sin[s\arctan tt\ln(-z)]}{(1+t^{2})^{s/2}\sinh(\pi t)}}dt,}$

   tamamlanmamış gama fonksiyonunun kullanılmasından kaçınır, ancak Re( s ) ≤ 0 ise bu integral pozitif reel eksen üzerindeki z için başarısız olur. Bu ifade 2 ^s Li _s (− z ) / (− z ) = Φ( yazılarak bulunur. z ² , s , ¹ ⁄ ₂ ) − z Φ( z ² , s , 1), burada Φ Lerch aşkındır ve Abel–Plana formülünü ilk Φ serisine ve 1 / ( e İkinci Φ serisine 1 / ( e ^{2 πt} − 1) yerine ^{2 πt} + 1) .
5. Belirtildiği gibi, sıradan geometrik serileri terimsel olarak aşağıdaki gibi integral alarak polilogaritma için bir integral ifade edebiliriz . ${\displaystyle s\in \mathbb {N} }$

   ${\displaystyle \operatöradı {Li} _{s+1}(z)={\frac {z\cdot (-1)^{s}}{s!}}\int _{0}^{1}{ \frac {\log ^{s}(t)}{1-tz}}dt.}$

Seri gösterimleri

1. Altında belirtildiği gibi yekpare temsilleri Yukarıdaki polylogarithm'e Bose-Einstein integral gösterimi negatif siparişleri için uzatılabilir s vasıtasıyla Hankel kontur entegrasyonu:

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=-{\Gamma (1-s) \over 2\pi i}\oint _{H}{(-t)^{ s-1} \over e^{t-\mu }-1}dt,}$

   burada H , Hankel konturudur, s ≠ 1, 2, 3, … ve integralin t = μ kutbu negatif olmayan gerçek eksen üzerinde yer almaz. Çevriti bu bulunacak şekilde modifiye edilebilir direkleri de integrali t - μ = 2 kπi ve entegre toplamı olarak değerlendirilebilir artıkları ( Wood 1992 , § 12, 13; Gradshteyn ve Ryzhik 1980 , § 9.553 ): harvnb hatası: hedef yok: CITEREFGradshteynRyzhik1980 ( yardım )

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=\Gamma (1-s)\sum _{k=-\infty }^{\infty }(2k\pi i-\ mu )^{s-1}.}$

   Bu, Re( s ) < 0 ve e ^μ = 1 hariç tüm μ için geçerli olacaktır. 0 < Im( μ ) ≤ 2 π için toplam şu şekilde bölünebilir:

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=\Gamma (1-s)\sol[(-2\pi i)^{s-1}\sum _{k= 0}^{\infty }\left(k+{\mu \over {2\pi i}}\sağ)^{s-1}+(2\pi i)^{s-1}\sum _{k =0}^{\infty }\sol(k+1-{\mu \over {2\pi i}}\sağ)^{s-1}\sağ],}$

   burada iki seri artık Hurwitz zeta işleviyle tanımlanabilir :

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1 -s}~\zeta \left(1-s,~{\mu \over {2\pi i}}\sağ)+i^{s-1}~\zeta \left(1-s,~1- {\mu \over {2\pi i}}\sağ)\sağ]\qquad (0<\operatöradı {Im} (\mu )\leq 2\pi )}$

   Yukarıda diğer fonksiyonlarla ilişkisi altında verilmiş olan bu bağıntı, tüm karmaşık s ≠ 0, 1, 2, 3, … için geçerlidir ve ilk olarak ( Jonquière 1889 , eq. 6) türetilmiştir .
2. Polilogaritmayı µ = 0 civarında bir kuvvet serisi olarak göstermek için , Hankel kontur integralinden türetilen seriyi şu şekilde yazıyoruz:

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\Gamma (1-s)\sum _ {h=1}^{\infty }\sol[(-2h\pi i-\mu )^{s-1}+(2h\pi i-\mu )^{s-1}\sağ].}$

   Toplamdaki iki terimli güçler µ = 0 civarında genişletildiğinde ve toplama sırası tersine çevrildiğinde, toplamın h üzeri kapalı biçimde ifade edilebilir:

   ${\displaystyle \operatöradı {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\sum _{k=0}^{ \infty }{\zeta (sk) \k üzerinde!}\mu ^{k}.}$

   Bu sonuç | µ | < 2 π ve tüm s ≠ 1, 2, 3, … için zeta fonksiyonları tarafından sağlanan analitik devamlılık sayesinde . Sıra pozitif bir tam sayı ise, s = n , toplamları olmasa da hem k = n − 1 olan terim hem de gama fonksiyonu sonsuz olur. Şunlar elde edilir ( Wood 1992 , § 9; Gradshteyn & Ryzhik 1980 , § 9.554 ): harvnb hatası: hedef yok: CITEREFGradshteynRyzhik1980 ( yardım )

   ${\displaystyle \lim _{s\to k+1}\left[{\zeta (sk) \over k!}\mu ^{k}+\Gamma (1-s)(-\mu )^{s -1}\sağ]={\mu ^{k} \over k!}\left[\sum _{h=1}^{k}{1 \h üzerinde}-\ln(-\mu )\sağ ],}$

   burada k = 0 ise h üzerindeki toplam ortadan kalkar. Yani, pozitif tamsayı mertebeleri için ve | μ | < 2 π dizimiz var:

   ${\displaystyle \operatöradı {Li} _{n}(e^{\mu })={\mu ^{n-1} \over (n-1)!}\left[H_{n-1}-\ ln(-\mu )\sağ]+\sum _{k=0,k\neq n-1}^{\infty }{\zeta (nk) \over k!}\mu ^{k},}$

   burada H _{, n} anlamına gelir n inci harmonik sayısı :

   ${\displaystyle H_{n}=\sum _{h=1}^{n}{1 \over h},\qquad H_{0}=0.}$

   Problem terimleri şimdi −ln(− μ ) içerir; bu, μ ^{n -1 ile} çarpıldığında , n = 1 dışında μ → 0 olarak sıfıra meyleder . Bu, Li _s ( z )' _nin gerçek bir logaritmik sergilediği gerçeğini yansıtır. tekillik de s = 1 ve z = 1 tarihi:

   ${\displaystyle \lim _{\mu \to 0}\Gamma (1-s)(-\mu )^{s-1}=0\qquad (\operatöradı {Re} (s)>1).}$

   İçin s yakındır, ancak eşit, olumlu tamsayıya, yaklaşık genişleme farklı terimler μ 0 hesaplama zorluklara neden beklenebilir = ( Ahşap 1992 , § 9). Erdélyi'nin ln( z )'nin kuvvetlerine karşılık gelen açılımı ( Erdélyi ve diğerleri 1981 , § 1.11-15) , polilogaritma ve logaritmanın ana dallarının aynı anda kullanıldığı varsayılırsa doğru değildir, çünkü ln( ¹ ⁄ _z ) eşit olarak −ln( z )'ye eşit değil . s'nin pozitif olmayan tamsayı değerleri için, yaklaşık µ = 0 açılımındaki zeta fonksiyonu ζ( s − k ) Bernoulli sayılarına indirgenir : ζ(− n − k ) = −B _{1+ n + k} / (1 + n + k ). Li _{- n} ( z )'nin bu seri tarafından sayısal olarak değerlendirilmesi, yukarıda belirli değerler altında verilen sonlu rasyonel ifadelerin büyük n için sergilediği iptal etkilerinden etkilenmez .
3. Kimlik kullanımı ile

   ${\displaystyle 1={1 \over \Gamma (s)}\int _{0}^{\infty }e^{-t}t^{s-1}dt\qquad (\operatorname {Re} (s )>0),}$

   polilogaritmanın Bose-Einstein integral gösterimi ( yukarıya bakın ) şu şekilde dökülebilir:

   ${\displaystyle \operatöradı {Li} _{s}(z)={\tfrac {1}{2}}z+{z \over 2\Gamma (s)}\int _{0}^{\infty }e ^{-t}t^{s-1}\coth {t-\ln z \over 2}dt\qquad (\operatöradı {Re} (s)>0).}$

   Hiperbolik kotanjantın ikili bir seri ile değiştirilmesi,

   ${\displaystyle \coth {t-\ln z \üzerinde}=2\toplam _{k=-\infty }^{\infty }^{\infty {1 \2k üzerinde\pi i+t-\ln z},}$

   daha sonra integral ve toplam sırasını tersine çevirerek ve son olarak toplamları üst tamamlanmamış gama fonksiyonunun integral bir temsili ile tanımlayarak , biri şunu elde eder:

   ${\displaystyle \operatöradı {Li} _{s}(z)={\tfrac {1}{2}}z+\sum _{k=-\infty }^{\infty }{\Gamma (1-s, 2k\pi i-\ln z) \over (2k\pi i-\ln z)^{1-s}}.}$

   Bu sonucun hem ikili serisi hem de hiperbolik kotanjant için, - k _max ile k _max arasındaki simetrik kısmi toplamlar koşulsuz olarak k _max → ∞ olarak yakınsar . Toplamın simetrik olarak gerçekleştirilmesi koşuluyla, Li _s ( z ) için bu seri böylece tüm karmaşık s için olduğu kadar tüm karmaşık z için de geçerlidir .
4. Pozitif olmayan tamsayı düzeninin polilogaritmasının sonlu toplamına ikinci türden Stirling sayıları için açık bir ifade ekleyerek ( yukarıya bakın ) şöyle yazılabilir:

   ${\displaystyle \operatöradı {Li} _{-n}(z)=\sum _{k=0}^{n}\left({-z \over 1-z}\sağ)^{k+1} \sum _{j=0}^{k}(-1)^{j+1}{k \j seçin}(j+1)^{n}\qquad (n=0,1,2,\ldots ).}$

   Basitçe dış toplamı ∞'ye genişleterek elde edilen sonsuz seri ( Guillera & Sondow 2008 , Teorem 2.1):

   ${\displaystyle \operatöradı {Li} _{s}(z)=\sum _{k=0}^{\infty }\left({-z \over 1-z}\right)^{k+1} ~\sum _{j=0}^{k}(-1)^{j+1}{k \j'yi seçin}(j+1)^{-s},}$

   kompleks için polylogarithm'e yakınsayacak çıkıyor s ve karmaşık için z Re ile ( Z ) < ¹ / ₂ için, kontrol edilebilir şekilde | ^{− z} ⁄ _{(1− z )} | < ¹ ⁄ ₂ toplama sırasını tersine çevirerek ve şunu kullanarak:

   ${\displaystyle \sum _{k=j}^{\infty }{k \j seçin}\left({-z \over 1-z}\right)^{k+1}=\left[\left( {-z \over 1-z}\sağ)^{-1}-1\sağ]^{-j-1}=(-z)^{j+1}.}$

   Bu serilerin iç katsayıları , genelleştirilmiş harmonik sayıları içeren Stirling sayılarıyla ilgili formüllerle ifade edilebilir . Örneğin , aşağıdaki kimliklerin kanıtlarını (kanıtlara referanslar) bulmak için işlev dönüşümleri oluşturmaya bakın :

   ${\displaystyle {\begin{aligned}\operatorname {Li} _{2}(z)&=\sum _{j\geq 1}{\frac {(-1)^{j-1}}{2} }\left(H_{j}^{2}+H_{j}^{(2)}\sağ){\frac {z^{j}}{(1-z)^{j+1}}} \\\operatöradı {Li} _{3}(z)&=\sum _{j\geq 1}{\frac {(-1)^{j-1}}{6}}\left(H_{j }^{3}+3H_{j}H_{j}^{(2)}+2H_{j}^{(3)}\sağ){\frac {z^{j}}{(1-z) ^{j+1}}}.\end{hizalı}}}$

   Re( z ) < ¹ ⁄ ₂ olan diğer argümanlar için sonucu analitik devam takip eder . Bu prosedür uygulanarak eşdeğerdir Euler dönüşümü serisi için z transandantı Polylogarithm tanımlar.

asimptotik açılımlar

için | z | ≫ 1, polilogaritma, ln(− z ) cinsinden asimptotik serilere genişletilebilir :

${\displaystyle \operatöradı {Li} _{s}(z)={\pm i\pi \over \Gamma (s)}[\ln(-z)\pm i\pi ]^{s-1}- \sum _{k=0}^{\infty }(-1)^{k}(2\pi )^{2k}{B_{2k} \fazla (2k)!}{[\ln(-z) \pm i\pi ]^{s-2k} \over \Gamma (s+1-2k)},}$

${\displaystyle \operatöradı {Li} _{s}(z)=\sum _{k=0}^{\infty }(-1)^{k}(1-2^{1-2k})(2 \pi )^{2k}{B_{2k} \fazla (2k)!}{[\ln(-z)]^{s-2k} \Gamma (s+1-2k)},}$

burada B _{2 k} , Bernoulli sayılarıdır . Her iki sürüm de tüm s ve herhangi bir arg( z ) için geçerlidir. Her zamanki gibi, terimler büyüklük olarak artmaya başladığında toplama sonlandırılmalıdır. Negatif tamsayı s için , açılımlar tamamen yok olur; negatif olmayan s tamsayıları için sonlu sayıda terimden sonra ayrılırlar. Wood (1992 , § 11), Bose-Einstein integral gösteriminden bu serileri elde etmek için bir yöntem açıklar (Li _s ( e ^µ ) için denklemi 11.2 , −2 π < Im( µ ) ≤ 0 gerektirir).

Sınırlayıcı davranış

Aşağıdaki limitler , polilogaritmaların çeşitli temsillerinden kaynaklanmaktadır ( Wood 1992 , § 22):

${\displaystyle \lim _{|z|\to 0}\operatöradı {Li} _{s}(z)=z}$

${\displaystyle \lim _{|\mu |\to 0}\operatöradı {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1 }\qquad (\operatöradı {Re} (s)<1)}$

${\displaystyle \lim _{\operatöradı {Re} (\mu )\to \infty }\operatöradı {Li} _{s}(\pm e^{\mu })=-{\mu ^{s} \ üzerinde \Gamma (s+1)}\qquad (s\neq -1,-2,-3,\ldots )}$

${\displaystyle \lim _{\operatöradı {Re} (\mu )\to \infty }\operatöradı {Li} _{-n}(e^{\mu })=-(-1)^{n}e ^{-\mu }\qquad (n=1,2,3,\ldots )}$

${\displaystyle \lim _{\operatöradı {Re} (s)\to \infty }\operatöradı {Li} _{s}(z)=z}$

${\displaystyle \lim _{\operatöradı {Re} (s)\to -\infty }\operatöradı {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}\qquad (-\pi <\operatöradı {Im} (\mu )<\pi )}$

${\displaystyle \lim _{\operatöradı {Re} (s)\to -\infty }\operatöradı {Li} _{s}(-e^{\mu })=\Gama (1-s)\left[ (-\mu -i\pi )^{s-1}+(-\mu +i\pi )^{s-1}\sağ]\qquad (\operatöradı {Im} (\mu )=0)}$

Wood'un Re( µ ) → ∞ için ilk limiti kendi denklemi 11.3'e göre düzeltildi. Re( s ) → −∞ için limit , polilogaritma ile Hurwitz zeta fonksiyonu arasındaki genel ilişkiden gelir ( yukarıya bakınız ).

Dilogaritma

Dilogaritma, s = 2 düzeyindeki polilogaritmasıdır. Keyfi karmaşık argüman z için dilogaritmanın alternatif bir integral ifadesi şudur ( Abramowitz & Stegun 1972 , § 27.7):

${\displaystyle \operatöradı {Li} _{2}(z)=-\int _{0}^{z}{\ln(1-t) \over t}dt=-\int _{0}^{ 1}{\ln(1-zt) \üzerinde t}dt.}$

Bir karışıklık kaynağı, bazı bilgisayar cebir sistemlerinin dilogaritmayı dilog( z ) = Li ₂ (1− z ) olarak tanımlamasıdır .

Gerçek z ≥ 1 durumunda, dilogaritmanın ilk integral ifadesi şu şekilde yazılabilir:

${\displaystyle \operatöradı {Li} _{2}(z)={\frac {\pi ^{2}}{6}}-\int _{1}^{z}{\ln(t-1) \n t}dt-i\pi \ln z} üzerinde$

ln( t −1) 'i genişleterek ve terim terim integral alarak elde ederiz.

${\displaystyle \operatöradı {Li} _{2}(z)={\frac {\pi ^{2}}{3}}-{\frac {1}{2}}(\ln z)^{2 }-\sum _{k=1}^{\infty }üzerinde k^{2}z^{k}}-i\pi \ln z\qquad (z\geq 1).}$

Abel kimlik dilogarithm için (verilir 1881 Abel )

${\displaystyle \operatöradı {Li} _{2}\left({\frac {x}{1-y}}\sağ)+\operatöradı {Li} _{2}\left({\frac {y}{ 1-x}}\sağ)-\operatöradı {Li} _{2}\left({\frac {xy}{(1-x)(1-y)}}\sağ)=\operatöradı {Li} _ {2}(x)+\operatöradı {Li} _{2}(y)+\ln(1-x)\ln(1-y)}$

${\displaystyle (\operatöradı {Re} (x)\leq {\tfrac {1}{2}}\wedge \operatöradı {Re} (y)\leq {\tfrac {1}{2}}\vee \operatöradı {Im} (x)>0\wedge \operatöradı {Im} (y)>0\vee \operatöradı {Im} (x)<0\wedge \operatöradı {Im} (y)<0\vee \ldots ). }$

Bunun x = 0 veya y = 0 için geçerli olduğu hemen görülür ve daha sonra genel argümanlar için ∂/∂ x ∂/∂ y türeviyle kolayca doğrulanır . İçin y = 1 x kimlik azaltır Euler 'in yansıma formül

${\displaystyle \operatöradı {Li} _{2}\left(x\sağ)+\operatöradı {Li} _{2}\left(1-x\sağ)={\frac {1}{6}}\ pi ^{2}-\ln(x)\ln(1-x),}$

burada Li ₂ (1) = ζ(2) = ¹ ⁄ ₆ π ² kullanılmıştır ve x herhangi bir karmaşık değeri alabilir.

u = x /(1− y ), v = y /(1− x ) yeni değişkenleri açısından Abel kimliği okur

${\displaystyle \operatöradı {Li} _{2}(u)+\operatöradı {Li} _{2}(v)-\operatöradı {Li} _{2}(uv)=\operatöradı {Li} _{2 }\left({\frac {u-uv}{1-uv}}\sağ)+\operatöradı {Li} _{2}\left({\frac {v-uv}{1-uv}}\sağ )+\ln \left({\frac {1-u}{1-uv}}\sağ)\ln \left({\frac {1-v}{1-uv}}\sağ),}$

bu , ( Rogers 1907 )'de verilen beşgen kimliğine karşılık gelir .

x = y = 1− z için Abel özdeşliğinden ve Landen özdeşliğine sahip olduğumuz kare ilişkiden

${\displaystyle \operatöradı {Li} _{2}(1-z)+\operatöradı {Li} _{2}\left(1-{\frac {1}{z}}\sağ)=-{\frac {1}{2}}(\ln z)^{2}\qquad (z\not \in ~]-\infty ;0]),}$

ve yansıma formülünü her bir dilogarimaya uygulayarak ters çevirme formülünü buluruz

${\displaystyle \operatöradı {Li} _{2}(z)+\operatöradı {Li} _{2}(1/z)=-{\tfrac {1}{6}}\pi ^{2}-{ \tfrac {1}{2}}[\ln(-z)]^{2}\qquad (z\değil [0;1[),}$

ve ayrıca gerçek z ≥ 1 için

${\displaystyle \operatöradı {Li} _{2}(z)+\operatöradı {Li} _{2}(1/z)={\tfrac {1}{3}}\pi ^{2}-{\ tfrac {1}{2}}(\ln z)^{2}-i\pi \ln z.}$

Özel argümanlarda dilogaritmanın bilinen kapalı biçimli değerlendirmeleri aşağıdaki tabloda toplanmıştır. İlk sütundaki Argümanlar yansıması ile ilgili X ↔ 1- X ya da ters çevirme x ↔ ¹ / _X ya x = 0 veya x = 1; üçüncü sütundaki argümanların tümü bu işlemlerle birbiriyle ilişkilidir.

Maximon (2003) , 17. ila 19. yüzyıl referanslarını tartışıyor. Yansıma formülü, Euler'in 1768 tarihli bir kitabında ( Maximon 2003 , § 10) ortaya çıkmasından önce, 1760'da Landen tarafından zaten yayınlanmıştı ; Abel'ın kimliğine bir eşdeğer , 1809'da Spence tarafından , Abel 1826'da elyazmasını yazmadan önce yayınlanmıştı ( Zagier 1989 , § 2). Bilogarithmische Function tanımı , Carl Johan Danielsson Hill (Lund, İsveç'te profesör) tarafından 1828'de tanıtıldı ( Maximon 2003 , § 10). Don Zagier  ( 1989 ), dilogaritmanın mizah duygusuna sahip tek matematiksel fonksiyon olduğunu belirtmiştir.

Dilogaritmanın özel değerleri

${\görüntüleme stili x}$	${\displaystyle \operatöradı {Li} _{2}(x)}$	${\görüntüleme stili x}$	${\displaystyle \operatöradı {Li} _{2}(x)}$
${\görüntüleme stili -1}$	${\displaystyle -{\tfrac {1}{12}}\pi ^{2}}$	${\görüntüleme stili -\phi }$	${\displaystyle -{\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\phi }$
${\görüntüleme stili 0}$	${\görüntüleme stili 0}$	${\görüntüleme stili -1/\fi }$	${\displaystyle -{\tfrac {1}{15}}\pi ^{2}+{\tfrac {1}{2}}\ln ^{2}\phi }$
${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle {\tfrac {1}{12}}\pi ^{2}-{\tfrac {1}{2}}\ln ^{2}2}$	${\displaystyle 1/\phi ^{2}}$	${\displaystyle {\tfrac {1}{15}}\pi ^{2}-\ln ^{2}\phi }$
${\görüntüleme stili 1}$	${\displaystyle {\tfrac {1}{6}}\pi ^{2}}$	${\ Displaystyle 1/\phi }$	${\displaystyle {\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\phi }$
${\görüntüleme stili 2}$	${\displaystyle {\tfrac {1}{4}}\pi ^{2}-\pi i\ln 2}$	${\görüntüleme stili\phi }$	${\displaystyle {\tfrac {11}{15}}\pi ^{2}+{\tfrac {1}{2}}\ln ^{2}(-1/\phi )}$
		${\displaystyle \fi ^{2}}$	${\displaystyle -{\tfrac {11}{15}}\pi ^{2}-\ln ^{2}(-\phi )}$

Burada altın oranı ifade etmektedir .${\displaystyle \phi ={\tfrac {1}{2}}({\sqrt {5}}+1)}$

polilogaritma merdivenleri

Leonard Lewin , özel değerler için polilogaritma üzerinde bir dizi klasik ilişkinin dikkate değer ve geniş bir genellemesini keşfetti. Bunlara artık polilogaritma merdivenleri deniyor . Altın oranın karşılığı olarak tanımlayın . O zaman iki basit dilogaritma merdiveni örneği ${\displaystyle \rho ={\tfrac {1}{2}}({\sqrt {5}}-1)}$

${\displaystyle \operatöradı {Li} _{2}(\rho ^{6})=4\operatöradı {Li} _{2}(\rho ^{3})+3\operatöradı {Li} _{2} (\rho ^{2})-6\operatöradı {Li} _{2}(\rho )+{\tfrac {7}{30}}\pi ^{2}}$

Coxeter  ( 1935 ) tarafından verilen ve

${\displaystyle \operatöradı {Li} _{2}(\rho )={\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\rho }$

Landen tarafından verildi . Polylogaritma merdivenleri, K-teorisi ve cebirsel geometride doğal ve derinden oluşur . Polylogaritma merdivenleri, BBP algoritması aracılığıyla çeşitli matematiksel sabitlerin hızlı hesaplanması için temel sağlar ( Bailey, Borwein & Plouffe 1997 ).

monodromi

Polilogaritma iki dal noktasına sahiptir ; biri z = 1'de ve diğeri z = 0'da. z = 0'daki ikinci dal noktası polilogaritma ana sayfasında görünmez; ancak işlev analitik olarak diğer sayfalarına devam ettirildiğinde görünür hale gelir . Monodromy polylogarithm'e grup oluşur Homotopy yaklaşık iki dal noktalarını rüzgar döngüler sınıfları. Bu ikisini m ₀ ve m ₁ ile ifade eden monodromi grup, grup sunumuna sahiptir.

${\displaystyle \langle m_{0},m_{1}\vert w=m_{0}m_{1}m_{0}^{-1}m_{1}^{-1},wm_{1}= m_{1}w\rangle .}$

Dilogarithm özel durum için, bir de bu sahiptir wm ₀ = m ₀ ağırlık ve monodromy grup haline gelir Heisenberg grubu (belirlenmesi m, ₀ , m ₁ ve W ile x , y , z ) ( 2008 Vepstas ).

Referanslar

• Abel, NH (1881) [1826]. "İşlevselliği not edin " ${\displaystyle \scriptstyle \psi x=x+{\frac {x^{2}}{2^{2}}}+{\frac {x^{3}}{3^{2}}}+\cdots +{\frac {x^{n}}{n^{2}}}+\cdots }$ (PDF) . Sylow'da, L.; Lie, S. (ed.). Niels Henrik Abel - Nouvelle edition, Tome II (Fransızca). Christiania [Oslo]: Grøndahl & Søn. s. 189–193. (Bu 1826 el yazması sadece ölümünden sonra yayınlandı.)
• Abramowitz, M.; Stegun, IA (1972). Formüller, Grafikler ve Matematik Tabloları ile Matematiksel Fonksiyonlar El Kitabı . New York: Dover Yayınları. ISBN'si 978-0-486-61272-0.
• Apostol, TM (2010), "Polylogarithm" , Olver , Frank WJ'de ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR  2723248
• Bailey, DH ; Borwein, PB ; Plouffe, S. (Nisan 1997). "Çeşitli Polilogaritmik Sabitlerin Hızlı Hesaplanması Üzerine" (PDF) . Hesaplama Matematiği . 66 (218): 903-913. Bibcode : 1997MaCom..66..903B . doi : 10.1090/S0025-5718-97-00856-9 .
• Bailey, DH; Broadhurst, DJ (20 Haziran 1999). "Onyedinci Dereceden Çoklogaritma Merdiveni". arXiv : matematik.CA/9906134 .
• Berndt, M.Ö. (1994). Ramanujan'ın Defterleri, Bölüm IV . New York: Springer-Verlag. s. 323–326. ISBN'si 978-0-387-94109-7.
• Boersma, J .; Dempsey, JP (1992). "Legendre'nin ki-fonksiyonunun değerlendirilmesi üzerine" . Hesaplama Matematiği . 59 (199): 157-163. doi : 10.2307/2152987 . JSTOR  2152987 .
• Borwein, D .; Borwein, JM ; Girgensohn, R. (1995). "Euler toplamlarının açık değerlendirmesi" (PDF) . Edinburgh Matematik Derneği Bildirileri . Seri 2. 38 (2): 277–294. doi : 10.1017/S0013091500019088 .
• Borwein, JM; Bradley, DM; Broadhurst, DJ; Lisonek, P. (2001). "Çoklu Polilogaritmaların Özel Değerleri". Amerikan Matematik Derneği'nin İşlemleri . 353 (3): 907-941. arXiv : matematik/9910045 . doi : 10.1090/S0002-9947-00-02616-7 . S2CID  11373360 .
• Broadhurst, DJ (21 Nisan 1996). "İndirgenemez k-kat Euler toplamlarının numaralandırılması ve düğüm teorisi ve alan teorisindeki rolleri üzerine". arXiv : hep-th/9604128 .
• Clunie, J. (1954). "Bose-Einstein fonksiyonları Üzerine". Fizik Topluluğunun Bildirileri . Seri A. 67 (7): 632-636. Bibcode : 1954PPSA...67..632C . doi : 10.1088/0370-1298/67/7/308 .
• Cohen, H.; Lewin, L.; Zagier, D. (1992). "Onaltıncı Dereceden Çoklogaritma Merdiveni" (PS) . Deneysel Matematik . 1 (1): 25–34.
• Coxeter, HSM (1935). "Schläfli ve Lobatschefsky'nin işlevleri". Üç Aylık Matematik Dergisi . 6 (1): 13–29. Bibcode : 1935QJMat...6...13C . doi : 10.1093/qmath/os-6.1.13 . JFM  61.0395.02 .
• Cvijovic, D.; Klinowski, J. (1997). "Riemann zeta fonksiyonu ve polilogaritmalar için sürekli kesir açılımları" (PDF) . Amerikan Matematik Derneği Bildirileri . 125 (9): 2543–2550. doi : 10.1090/S0002-9939-97-04102-6 .
• Cvijovic, D. (2007). "Çok logaritma fonksiyonunun yeni integral gösterimleri". Kraliyet Cemiyeti A Bildirileri . 463 (2080): 897–905. arXiv : 0911.4452 . Bibcode : 2007RSPSA.463..897C . doi : 10.1098/rspa.2006.1794 . S2CID  115156743 .
• Erdelyi, A. ; Magnus, W.; Oberhettinger, F.; Tricomi, FG (1981). Daha Yüksek Aşkın Fonksiyonlar, Cilt. 1 (PDF) . Malabar, FL: RE Krieger Yayıncılık. ISBN'si 978-0-89874-206-0. (Bu, 1953 tarihli McGraw-Hill orijinalinin yeniden basımıdır.)
• Fornberg, B.; Kölbig, KS (1975). "Jonquière veya polilogaritma fonksiyonunun karmaşık sıfırları" . Hesaplama Matematiği . 29 (130): 582-599. doi : 10.2307/2005579 . JSTOR  2005579 .
• GNU Bilimsel Kütüphanesi (2010). "Başvuru Kılavuzu" . 2010-06-13 alındı .
• Gradshteyn, Izrail Solomonovich ; Ryzhik, Iosif Moiseevich ; Geronimus, Yuri Veniaminovich ; Tseytlin, Mihail Yulyeviç ; Jeffrey, Alan (2015) [Ekim 2014]. "9.553." Zwillinger'de Daniel; Moll, Victor Hugo (ed.). İntegraller, Seriler ve Ürünler Tablosu . Scripta Technica, Inc. tarafından çevrilmiştir (8 ed.). Academic Press, Inc. s. 1050. ISBN 978-0-12-384933-5. LCCN  2014010276 .
• Guillera, J.; Sondow, J. (2008). "Çift integraller ve bazı klasik sabitler için Lerch'in aşkınlığının analitik devamı yoluyla sonsuz ürünler". Ramanujan Dergisi . 16 (3): 247–270. arXiv : matematik.NT/0506319 . doi : 10.1007/s11139-007-9102-0 . S2CID  119131640 .
• Hain, RM (25 Mart 1992). "Klasik polilogaritmalar". arXiv : alg-geom/9202022 .
• Jahnke, E.; Emde, F. (1945). Formüller ve Eğriler ile Fonksiyon Tabloları (4. baskı). New York: Dover Yayınları.
• Jonquiere, A. (1889). "Not sur la série " ${\displaystyle \scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{s}}}}$ (PDF) . Bulletin de la Société Mathématique de France (Fransızca). 17 : 142–152. doi : 10.24033/bsmf.392 . JFM  21.0246.02 .
• Kölbig, KS; Mignaco, JA; Remiddi, E. (1970). "Nielsen'in genelleştirilmiş polilogaritmaları ve sayısal hesaplamaları üzerine" . BIT . 10 : 38-74. doi : 10.1007/BF01940890 . S2CID  119672619 .
• Kirillov, AN (1995). "Dilogaritma kimlikleri". Teorik Fizik Ekinin Gelişimi . 118 : 61-142. arXiv : hep-th/9408113 . Bibcode : 1995PThPS.118...61K . doi : 10.1143/PTPS.118.61 . S2CID  119177149 .
• Lewin, L. (1958). Dilogaritmalar ve İlişkili Fonksiyonlar . Londra: Macdonald. MR  0105524 .
• Lewin, L. (1981). Polylogaritmalar ve İlişkili Fonksiyonlar . New York: Kuzey Hollanda. ISBN'si 978-0-444-00550-2.
• Lewin, L., ed. (1991). Polilogaritmaların Yapısal Özellikleri . Matematiksel Araştırmalar ve Monograflar. 37 . Providence, RI: Amer. Matematik. Soc. ISBN'si 978-0-8218-1634-9.
• Markman, B. (1965). "Riemann Zeta İşlevi". BIT . 5 : 138–141.
• Maximon, LC (2003). "Karmaşık Argüman için Dilogaritma Fonksiyonu". Kraliyet Cemiyeti A Bildirileri . 459 (2039): 2807-2819. Bibcode : 2003RSPSA.459.2807M . doi : 10.1098/rspa.2003.1156 . S2CID  122271244 .
• McDougall, J.; Stoner, EC (1938). "Fermi-Dirac fonksiyonlarının hesaplanması" . Royal Society A'nın Felsefi İşlemleri . 237 (773): 67–104. Bibcode : 1938RSPTA.237...67M . doi : 10.1098/rsta.1938.0004 . JFM  64.1500.04 .
• Nielsen, N. (1909). "Der Eulersche Dilogarithmus und seine Verallgemeinerungen. Eine Monographie". Nova Acta Leopoldina (Almanca). Halle – Leipzig, Almanya: Kaiserlich-Leopoldinisch-Carolinische Deutsche Akademie der Naturforscher. XC (3): 121–212. JFM  40.0478.01 .
• Prudnikov, AP; Marichev, OI; Brychkov, Yu.A. (1990). İntegraller ve Seriler, Cilt. 3: Daha Fazla Özel Fonksiyonlar . Newark, NJ: Gordon ve İhlal. ISBN'si 978-2-88124-682-1. (bkz. § 1.2, "Genelleştirilmiş zeta fonksiyonu, Bernoulli polinomları, Euler polinomları ve polilogaritmalar", s. 23.)
• Robinson, JE (1951). "Bose-Einstein integral fonksiyonları üzerine not". Fiziksel İnceleme . Seri 2. 83 (3): 678–679. Bibcode : 1951PhRv...83..678R . doi : 10.1103/PhysRev.83.678 .
• Rogers, LJ (1907). "Serilerle bağlantılı fonksiyon toplamı teoremleri hakkında "${\displaystyle \scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{2}}}}$ . Londra Matematik Derneği Bildirileri (2) . 4 (1): 169–189. doi : 10.1112/plms/s2-4.1.169 . JFM  37.0428.03 .
• Schrödinger, E. (1952). İstatistiksel Termodinamik (2. baskı). Cambridge, Birleşik Krallık: Cambridge University Press.
• Truesdell, C. (1945). "Polimerlerin yapısı teorisinde meydana gelen bir fonksiyon üzerine". Matematik Annals . İkinci Seri. 46 (1): 144–157. doi : 10.2307/1969153 . JSTOR  1969153 .
• Vepstas, L. (2008). "Salınım serilerinin yakınsamasını hızlandırmak için etkili bir algoritma, polilogaritma ve Hurwitz zeta fonksiyonlarının hesaplanması için faydalı". Sayısal Algoritmalar . 47 (3): 211-252. arXiv : matematik.CA/0702243 . Bibcode : 2008NuAlg..47..211V . doi : 10.1007/s11075-007-9153-8 . S2CID  15131811 .
• Whittaker, ET ; Watson, GN (1927). Modern Analiz Kursu (4. baskı). Cambridge, Birleşik Krallık: Cambridge University Press.(bu basım birçok kez yeniden basılmıştır, 1996 ciltsiz bir cilt ISBN  0-521-09189-6'ya sahiptir .)
• Wirtinger, W. (1905). "Über eine besondere Dirichletsche Reihe". Journal für die Reine und Angewandte Mathematik (Almanca). 1905 (129): 214-219. doi : 10.1515/crl.1905.129.214 . JFM  37.0434.01 . S2CID  199545536 .
• Wood, DC (Haziran 1992). "Polylogaritmaların Hesaplanması. Teknik Rapor 15-92*" (PS) . Canterbury, Birleşik Krallık: Kent Üniversitesi Bilgi İşlem Laboratuvarı . 2005-11-01 alındı .
• Zagier, D. (1989). "Geometri ve sayı teorisinde dilogaritma işlevi". Sayı Teorisi ve İlgili Konular: Ramanujan Kolokyumunda sunulan bildiriler, Bombay, 1988 . Matematik Çalışmaları. 12 . Bombay: Tata Temel Araştırma Enstitüsü ve Oxford University Press. s. 231–249. ISBN'si 0-19-562367-3.(aynı zamanda Journal of Mathematical and Physical Sciences 22 (1988), s. 131-145'te ve ( Zagier 2007 ) Bölüm I olarak "The olağanüstü dilogaritm" olarak göründü .)
• Zagier, D. (2007). "Dilogaritma İşlevi" (PDF) . Cartier, PE'de; ve diğerleri (ed.). Sayı Teorisi, Fizik ve Geometride Sınırlar II – Uygun Alan Teorileri, Ayrık Gruplar ve Renormalizasyon Üzerine . Berlin: Springer-Verlag. s. 3-65. ISBN'si 978-3-540-30307-7.

Dış bağlantılar

• Weisstein, Eric W. "Polilogaritma" . Matematik Dünyası .
• Weisstein, Eric W. "Dilogaritma" . Matematik Dünyası .
• Analitik Sayı Teorisindeki Algoritmalar, keyfi kesinlikte, GMP tabanlı, GPL lisanslı bir uygulama sağlar.