Tek grafik - Odd graph

Tek grafik
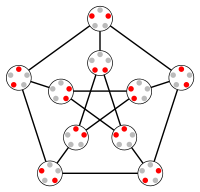
O 3 = KG 5,2 Petersen grafiğidir
tepe noktaları	${\displaystyle {\tbinom {2n-1}{n-1}}}$
Kenarlar	${\displaystyle n{\tbinom {2n-1}{n-1}}/2}$
Çap	n  - 1
çevre	3 n = 2 ise 5 n = 3 ise 6 n > 3 ise
Özellikler	mesafe geçişli
gösterim	O n
Grafikler ve parametreler tablosu

Tek grafik O ₄ = KG _7,3

Olarak matematiksel alanında grafik teorisi , tek grafikleri O _{, n} ailesidir simetrik grafikler yüksek olan tek çevresi bazı tanımlanmış, ayar sistemleri . Petersen grafiğini içerir ve genelleştirirler .

Tanım ve örnekler

Tek grafiği O _n ,  (2 n  − 1) elemanlı bir kümenin ( n − 1) elemanlı alt kümelerinin her biri için bir tepe noktasına sahiptir . İki köşe, ancak ve ancak karşılık gelen alt kümeler ayrık ise bir kenarla bağlanır . Diğer bir deyişle, O _{, n} olduğu Kneser grafiktir KG (2 , n  - 1, n  - 1).

O ₂ bir üçgen, O ₃ ise bilinen Petersen grafiğidir .

Jeneralize tek grafikler gibi tanımlanmıştır mesafe normal grafikler ile çapı n  1 ve tek çevresi 2 - n  - 1 bazıları için n . Tek grafikleri ve katlanmış küp grafiklerini içerirler .

Tarih ve uygulamalar

Petersen, grafik 1898 yılından bu yana bilinmesine karşın, çalışmalarına bir tek grafik tarihleri gibi tanımı Kowalewski (1917) , aynı zamanda tek grafik incelenen, O ₄ . Tek grafikler , karbonyum iyonlarının kaymalarının modellenmesinde, kimyasal grafik teorisindeki uygulamaları için incelenmiştir . Ayrıca olarak önerilmiştir ağ topolojisi olarak paralel işlem .

Gösterimde O _{, n} , bu grafikler için tarafından tanıtılan Norman Biggs 1972 Biggs ve Tony Gardiner 1974 yayınlanmamış bir el yazması tek grafiklerin adı açıklar: bir tek grafik her kenar eşsiz elemanı atanabilir X bir " garip adam dışarı ", yani, o kenara gelen köşelerle ilişkili her iki alt kümenin üyesi değil.

Özellikler

Tek grafiği O _n , n derecesinde düzenlidir . Bu sahiptir köşeleri ve kenarları. Bu nedenle, n = 1, 2,... için köşe sayısı${\displaystyle {\tbinom {2n-1}{n-1}}}$${\displaystyle n{\tbinom {2n-1}{n-1}}/2}$

Mesafe ve simetri

O _n'deki iki köşe , bir kümeden k elemanın çıkarılması ve k farklı elemanın eklenmesiyle birbirinden farklı olan kümelere karşılık geliyorsa , bu durumda , her bir çifti birer birer gerçekleştiren 2 k adımda birbirinden ulaşılabilir. tek ekleme ve çıkarma. 2 k  <  n ise , bu en kısa yoldur ; aksi takdirde, birinci kümeden ikinciyi tamamlayan bir kümeye bu tür bir yol bulmak ve daha sonra bir adımda ikinci kümeye ulaşmak daha kısadır. Bu nedenle, çap arasında O _{, n} olup , n  - 1.

Her tek grafik 3-yay geçişlidir : tek bir grafikteki her yönlendirilmiş üç kenarlı yol, grafiğin simetrisi ile bu tür diğer yollara dönüştürülebilir. Tek grafikler mesafe geçişlidir , dolayısıyla mesafe düzenlidir . Uzaklık düzenli grafikler olarak, kesişim dizileri tarafından benzersiz bir şekilde tanımlanırlar: başka hiçbir mesafe düzenli grafik, tek bir grafikle aynı parametrelere sahip olamaz. Bununla birlikte, yüksek derecede simetrilerine rağmen, n  > 2 için O _n tek grafikleri asla Cayley grafikleri değildir .

Tek grafikler düzenli ve kenar geçişli olduğundan, köşe bağlantıları derecelerine eşittir, n .

n > 3 olan tek grafiklerin çevresi altıdır; ancak, ikili grafikler olmasalar da , tek döngüleri çok daha uzundur. Özel olarak, tek grafik O _{, n} sahip tek çevresi 2 N  - 1. Bir ise n -Ücretli grafik bir çapa sahiptir , n  - 1 ve tek çevresi 2 , n  - 1, işlem sadece , n ayrı öz , bu mesafe normal olmalıdır. Çapı n  − 1 ve tek çevresi 2 n  − 1 olan uzaklık-düzenli grafikler , genelleştirilmiş tek grafikler olarak bilinir ve tek grafiklerin yanı sıra katlanmış küp grafiklerini de içerir .

Bağımsız kümeler ve köşe renklendirme

Let O _{, n} , bir (2 altkümelerinden tanımlanan bir tek grafik olarak n  - 1) -eleman grubu X ve izin X herhangi bir üyesi olabilir , X . O zaman, O _n'nin köşeleri arasında , tam olarak x içeren kümelere karşılık gelir  . Tüm bu kümeler x içerdiğinden , ayrık değildirler ve bağımsız bir O _n kümesi oluştururlar . Yani, O _n'nin 2 n  − 1 farklı bağımsız boyut kümesi vardır . İzler erdos-Ko-Rado teoremi bu olduğuna maksimum bağımsız setleri arasında O _n . yani, bağımsızlık sayısı arasında O _n olduğu böylece Ayrıca, her maksimum bağımsız küme, bu formu olmalıdır O _n tam 2 sahiptir n  1 maksimum bağımsız setleri -. ${\displaystyle {\tbinom {2n-2}{n-2}}}$${\displaystyle {\tbinom {2n-2}{n-2}}}$${\görüntüleme stili {\tbinom {2n-2}{n-2}}.}$

Eğer ben ihtiva setleri oluşturduğu maksimum bağımsız setidir x , daha sonra tamamlayıcı bir I içermeyen köşeler kümesidir x . Bu tamamlayıcı küme , G'de bir eşleşmeye neden olur . Bağımsız kümenin her köşesi, eşleşmenin n köşesine bitişiktir ve eşleşmenin her köşesi  , bağımsız kümenin n - 1 köşesine bitişiktir . Bu ayrıştırma nedeniyle ve tek grafikler iki parçalı olmadığından, üç numaralı kromatik vardır : maksimum bağımsız kümenin tepe noktalarına tek bir renk atanabilir ve tamamlayıcı eşleşmeyi renklendirmek için iki renk daha yeterlidir.

Kenar boyama

Tarafından Vizing teoremi , gerekli renk sayısı kenarları renk tek Grafik, O _{, n} , ya olduğu , n ve n  + 1 ve durumunda Petersen, grafik O ₃ bu olup , n  + 1 N ikinin bir gücü olan , grafikteki köşe sayısı tektir ve buradan yine kenar renklerinin sayısının n  + 1 olduğu sonucu çıkar . Bununla birlikte, O ₅ , O ₆ ve O _7'nin her biri n renkle kenar renkli olabilir .

Biggs bu sorunu şu hikayeyle açıklıyor: Kurgusal Croam kasabasındaki on bir futbolcu , 1386 olası yolla beş kişilik takımlar (tek bir adam hakem olarak görev yapacak) oluşturmak istiyor ve planlamak istiyorlar. Her bir çift arasındaki maçlar, her takım için altı oyun haftanın altı farklı gününde oynanacak ve tüm takımlar için Pazar günleri tatil olacak şekilde oynanır. Bunu yapabilmek mümkün mü? Bu hikayede, her oyun O _6'nın bir kenarını temsil eder , haftanın her günü bir renkle temsil edilir ve O _{6'nın 6} renkli kenar boyaması , oyuncuların zamanlama sorununa bir çözüm sağlar.

Hamiltoniklik

Petersen grafiği O ₃ iyi bilinen bir Hamilton olmayan grafiktir, ancak n  ≥ 4 için tüm O _n tek grafiklerinin bir Hamilton döngüsüne sahip olduğu bilinmektedir. Tek grafikler tepe-geçişli olduğundan , Lovász'ın varsayımına olumlu bir yanıtın bilindiği özel durumlardan biridir. Biggs, daha genel olarak, O _n'nin kenarlarının, kenardan ayrık Hamiltonyen döngülerine bölünebileceğini tahmin etti . Zaman n, tek sayı, kalan kenarları daha sonra tam bir uyum meydana gerekir. Bu güçlü varsayım için doğrulandı n = 4, 5, 6, 7 için , n  = 8, tepe nokta tek sayı O _{, n} önler mevcut gelen boyama 8 renkli kenar, ancak bir bölme olasılığını dışlamaz dört Hamilton çevrimi. ${\displaystyle \lfloor n/2\rfloor }$

Referanslar

Dış bağlantılar

• Weisstein, Eric W. , "Tek Grafik" , MathWorld