LC devresi - LC circuit
| Doğrusal analog elektronik filtreler |
|---|

Bir LC devresi de denir, rezonans devresi , tank devresi veya ayarlı devre , bir bir elektrik devresinin bir oluşan indüktör L harfi ile temsil edilen, ve bir kondansatör birbirine bağlı C harfi ile temsil edilen,. Devre , devrenin rezonans frekansında salınan enerjiyi depolayan , bir akort çatalının elektriksel bir analogu olan bir elektrik rezonatörü olarak hareket edebilir .
LC devreleri, ya belirli bir frekansta sinyal üretmek ya da daha karmaşık bir sinyalden belirli bir frekansta bir sinyal seçmek için kullanılır; bu işleve bant geçiren filtre denir . Osilatörler , filtreler , tunerler ve frekans karıştırıcıları gibi devrelerde kullanılan birçok elektronik cihazda, özellikle radyo ekipmanında anahtar bileşenlerdir .
Bir LC devresi, direnç nedeniyle enerji kaybı olmadığını varsaydığı için idealleştirilmiş bir modeldir . Bir LC devresinin herhangi bir pratik uygulaması, her zaman bileşenler ve bağlantı kabloları içindeki küçük ama sıfır olmayan dirençten kaynaklanan kaybı içerecektir. Bir LC devresinin amacı genellikle minimum sönümleme ile salınım yapmaktır , böylece direnç mümkün olduğu kadar düşük yapılır. Hiçbir pratik devre kayıpsız olmasa da, anlayış ve fiziksel sezgi kazanmak için devrenin bu ideal biçimini incelemek yine de öğreticidir. Direnç içeren bir devre modeli için, bkz. RLC devresi .
terminoloji
Yukarıda açıklanan iki elemanlı LC devresi, indüktör-kapasitör ağının (veya LC ağının ) en basit türüdür . Daha fazla indüktör ve kapasitör içeren daha karmaşık (yüksek dereceli) LC ağlarından ayırt etmek için ikinci dereceden bir LC devresi olarak da adlandırılır . İkiden fazla reaktansa sahip bu tür LC ağları, birden fazla rezonans frekansına sahip olabilir .
Ağın sırası , karmaşık frekans değişkeni s'de ağı tanımlayan rasyonel fonksiyonun sırasıdır . Genellikle sıra devredeki L ve C elemanlarının sayısına eşittir ve hiçbir durumda bu sayıyı aşamaz.
Operasyon
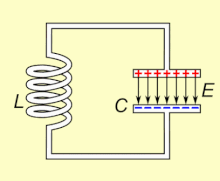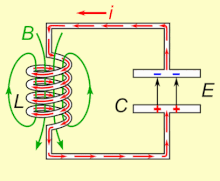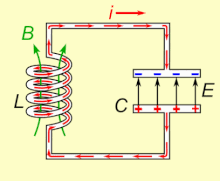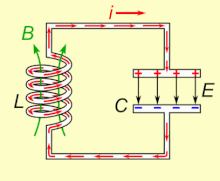
Doğal rezonans frekansında salınan bir LC devresi elektrik enerjisini depolayabilir . Animasyona bakın. Bir kapasitör , üzerindeki voltaja bağlı olarak plakaları arasındaki elektrik alanında ( E ) enerji depolar ve bir indüktör , içinden geçen akıma bağlı olarak enerjiyi manyetik alanında ( B ) depolar .
Yüklü bir kapasitöre bir indüktör bağlanırsa, kapasitördeki voltaj, indüktörden bir akım geçirerek etrafında bir manyetik alan oluşturur. Yük, akım akışı tarafından kullanıldığından, kapasitör üzerindeki voltaj sıfıra düşer. Bu noktada bobinin manyetik alanında depolanan enerji bobin boyunca bir voltaj indükler, çünkü indüktörler akımdaki değişikliklere karşı çıkar. Bu indüklenen voltaj, bir akımın kapasitörü orijinal yüküne zıt kutuplu bir voltajla yeniden şarj etmeye başlamasına neden olur. Nedeniyle Faraday yasası , EMF akımını yönlendiren manyetik alan azalmasına neden olur, böylece enerji kondansatör manyetik alandan çıkartılır şarj etmek gerekli. Manyetik alan tamamen dağıldığında, akım duracak ve yük, daha önce olduğu gibi zıt kutuplu olarak tekrar kapasitörde depolanacaktır. Ardından, akım indüktörden ters yönde akarken döngü tekrar başlayacaktır.
Yük, kondansatörün plakaları arasında indüktör boyunca ileri geri akar. Enerji, kondansatör ve indüktör arasında (harici bir devreden doldurulmadıysa) iç direnç salınımları yok edene kadar ileri geri salınır. Matematiksel olarak harmonik osilatör olarak bilinen ayarlı devrenin hareketi, bir sarkaçın ileri geri sallanmasına veya bir tankta suyun ileri geri sallanmasına benzer ; bu nedenle devreye tank devresi de denir . Doğal frekans (diğer sisteminden izole yukarıda tarif edildiği gibi olduğu, frekans ve bu noktada, salınmasına neden olur) kapasite ve indüktans değerleri ile tespit edilir. Çoğu uygulamada, ayarlı devre, kendisine alternatif akım uygulayan ve sürekli salınımlar sağlayan daha büyük bir devrenin parçasıdır . Uygulanan akımın frekansı devrenin doğal rezonans frekansıysa ( aşağıdaki doğal frekans ), rezonans meydana gelir ve küçük bir sürücü akımı, büyük genlikli salınım gerilimlerini ve akımlarını harekete geçirebilir. Elektronik ekipmandaki tipik ayarlı devrelerde salınımlar, saniyede binlerce ila milyarlarca kez çok hızlıdır.
rezonans etkisi
Rezonans , bir LC devresi, endüktif ve kapasitif reaktansların büyüklük olarak eşit olduğu bir açısal frekans ω 0'da harici bir kaynaktan sürüldüğünde meydana gelir . Bu eşitliğin belirli bir devre için geçerli olduğu frekansa rezonans frekansı denir. Rezonans frekansı LC devresinin olduğu
burada L bir endüktans olarak Henries ve Cı olduğu kapasite içinde farad . Açısal frekans ω 0 birimindedir radyan saniye.
Birimlerinde eşdeğer frekans Hertz olduğu
Uygulamalar
LC devresinin rezonans etkisi, sinyal işleme ve iletişim sistemlerinde birçok önemli uygulamaya sahiptir.
- Tank devrelerinin en yaygın uygulaması, radyo vericilerini ve alıcılarını ayarlamaktır . Örneğin, bir radyoyu belirli bir istasyona ayarlarken, LC devreleri o belirli taşıyıcı frekansı için rezonansa ayarlanır .
- Seri rezonans devresi voltaj büyütme sağlar .
- Paralel rezonans devresi akım büyütme sağlar .
- RF yükselticilerinin çıkış devrelerinde yük empedansı olarak paralel bir rezonans devresi kullanılabilir. Yüksek empedans nedeniyle, amplifikatörün kazancı rezonans frekansında maksimumdur.
- İndüksiyonlu ısıtmada hem paralel hem de seri rezonans devreleri kullanılır .
LC devreleri , birçok uygulamada önemli bir bileşen olan elektronik rezonatörler gibi davranır :
- amplifikatörler
- osilatörler
- Filtreler
- akortçular
- Mikserler
- Foster-Seeley ayrımcısı
- Temassız kartlar
- Grafik tabletler
- Elektronik makale gözetimi (güvenlik etiketleri)
Zaman alanı çözümü
Kirchhoff yasaları
Tarafından Kirchhoff gerilim hakları , gerilim V Cı kapasitör üzerindeki artı voltajı V L endüktörde sıfıra eşit olmalıdır:
Aynı şekilde, Kirchhoff'un akım yasasına göre , kapasitörden geçen akım, indüktörden geçen akıma eşittir:
Devre elemanlarının kurucu bağıntılarından da biliyoruz ki
diferansiyel denklem
Yeniden düzenleme ve değiştirme, ikinci dereceden diferansiyel denklemi verir
ω 0 parametresi , rezonans açısal frekansı şu şekilde tanımlanır:
Bunu kullanmak diferansiyel denklemi basitleştirebilir:
İlişkili Laplace dönüşümü IS
Böylece
nerede j olan hayali birim .
Çözüm
Böylece, diferansiyel denklemin tam çözümü
ve A ve B için başlangıç koşulları dikkate alınarak çözülebilir . Üstel karmaşık olduğundan, çözüm sinüzoidal bir alternatif akımı temsil eder . Elektrik akımı I fiziksel bir büyüklük olduğundan, gerçek değerli olmalıdır. Sonuç olarak, A ve B sabitlerinin karmaşık eşlenikler olması gerektiği gösterilebilir :
Şimdi izin ver
Öyleyse,
Daha sonra, kullanabilir Euler formülünü gerçek elde etmek üzere sinüzoit ile amplitüd I 0 , açısal frekans ω 0 = 1/√ LC, ve faz açısı .
Böylece, elde edilen çözüm olur
Başlangıç koşulları
Bu sonucu sağlayacak başlangıç koşulları şunlardır:
Seri devre
LC devresinin seri konfigürasyonunda, indüktör (L) ve kapasitör (C) burada gösterildiği gibi seri olarak bağlanır. Açık terminallerdeki toplam voltaj V , basitçe indüktör üzerindeki voltajın ve kapasitör üzerindeki voltajın toplamıdır. Devrenin pozitif terminaline giren akım I , hem kapasitör hem de indüktörden geçen akıma eşittir.
Rezonans
Frekans arttıkça endüktif reaktans büyüklüğü X L artarken, kapasitif reaktans büyüklüğü X C frekanstaki artışla azalır. Belirli bir frekansta, bu iki reaktans büyüklük olarak eşittir, ancak işaret olarak zıttır; bu frekansa verilen devre için rezonans frekansı f 0 denir .
Dolayısıyla rezonansta,
ω için çözerken , elimizde
devrenin rezonans açısal frekansı olarak tanımlanır. Açısal frekansı (saniyede radyan cinsinden) frekansa (hertz cinsinden) dönüştürmek,
Seri konfigürasyonda, X C ve X L birbirini iptal eder. Gerçekte, idealleştirilmiş bileşenlerden ziyade, akım, çoğunlukla bobin sargılarının direnciyle karşı karşıyadır. Bu nedenle, bir seri rezonans devresine sağlanan akım rezonansta maksimumdur.
- f → f 0 olarak limitte akım maksimumdur. Devre empedansı minimumdur. Bu durumda devreye alıcı devre denir.
- İçin f < f 0 , X, L «- X, C . Dolayısıyla devre kapasitiftir.
- İçin f > f 0 , X L »- X C . Dolayısıyla devre endüktiftir.
İç direnç
Seri konfigürasyonda, devrenin karmaşık elektrik empedansı sıfıra yaklaştığında rezonans meydana gelir.
İlk önce seri LC devresinin empedansını düşünün . Toplam empedans, endüktif ve kapasitif empedansların toplamı ile verilir:
Endüktif empedansı Z L = jωL ve kapasitif empedansı Z C = olarak yazma1/jωC ve yerine koyma verir
Bu ifadeyi ortak payda altında yazmak,
Son olarak, doğal açısal frekansı şu şekilde tanımlayın:
empedans olur
Pay, ω → ± ω 0 olarak limitte , toplam empedans Z'nin sıfır olacağını ve aksi takdirde sıfır olmayacağını ima eder . Bu nedenle seri LC devresi, bir yükle seri olarak bağlandığında , LC devresinin rezonans frekansında sıfır empedansa sahip bir bant geçiren filtre görevi görecektir .
Paralel devre
İndüktör (L) ve kapasitör (C) burada gösterildiği gibi paralel bağlandığında , açık terminallerdeki V gerilimi hem indüktör üzerindeki gerilime hem de kapasitör üzerindeki gerilime eşittir. Devrenin pozitif terminaline akan toplam akım I , indüktörden geçen akım ile kondansatörden geçen akımın toplamına eşittir:
Rezonans
X L , X C'ye eşit olduğunda , iki dal akımı eşit ve zıttır. Ana hatta minimum akım vermek için birbirlerini iptal ederler (prensipte sıfır akım). Ancak kondansatör ile indüktör arasında dolaşan büyük bir akım vardır. Prensipte, bu dolaşım akımı sonsuzdur, ancak gerçekte devredeki dirençle, özellikle de indüktör sargılarındaki dirençle sınırlıdır. Toplam akım minimum olduğundan, bu durumda toplam empedans maksimumdur.
Rezonans frekansı şu şekilde verilir:
Herhangi bir dal akımının rezonansta minimum olmadığını, ancak her birinin kaynak voltajının ( V ) reaktansa ( Z ) bölünmesiyle ayrı ayrı verildiğine dikkat edin . Dolayısıyla ben =V/Z, Ohm yasasına göre .
- En f 0 , hat akımı az. Toplam empedans maksimumdur. Bu durumda bir devreye rejektör devresi denir .
- f 0'ın altında devre endüktiftir.
- Yukarıda f , 0 , devre kapasitif.
İç direnç
Aynı analiz paralel LC devresine de uygulanabilir. Toplam empedans daha sonra tarafından verilir
ve Z L = jωL ve Z C = ikamesinden sonra1/jωC ve sadeleştirme, verir
kullanma
daha da basitleştirir
Bunu not et
ancak ω'nin diğer tüm değerleri için empedans sonludur. Bir yük ile seri olarak bağlanan paralel LC devresi , LC devresinin rezonans frekansında sonsuz empedansa sahip bant durdurucu filtre görevi görecektir . Bir yüke paralel bağlanan paralel LC devresi, bant geçiren filtre görevi görecektir .
Laplace çözümü
LC devresi Laplace dönüşümü ile çözülebilir .
Genel denklem şöyle olsun:
LC serisinin diferansiyel denklemi şöyle olsun:
Başlangıç koşulu ile:
Tanımlayalım:
verir:
Laplace ile dönüştürün:
Sonra antitransform:
Giriş voltajının Heaviside adım fonksiyonu olması durumunda :
Giriş voltajının sinüzoidal fonksiyon olması durumunda:
Tarih
Bir kapasitör ve indüktörün elektriksel salınımlar üretebileceğine dair ilk kanıt, 1826'da Fransız bilim adamı Felix Savary tarafından keşfedildi . Bir Leyden kavanozu demir bir iğnenin etrafına sarılmış bir telden boşaltıldığında, iğnenin bazen bir yönde, bazen de ters yönde manyetize kaldığını buldu. Bunun, iğnenin manyetizasyonunu bir etki olamayacak kadar küçük olana kadar ileri geri tersine çeviren ve iğneyi rastgele bir yönde mıknatıslanmış halde bırakan teldeki sönümlü salınımlı deşarj akımından kaynaklandığını doğru bir şekilde çıkardı. Amerikalı fizikçi Joseph Henry, Savary'nin deneyini 1842'de tekrarladı ve görünüşe göre bağımsız olarak aynı sonuca vardı. İrlandalı bilim adamı William Thomson (Lord Kelvin) 1853'te bir Leyden kavanozunun bir endüktans yoluyla boşalmasının salınımlı olması gerektiğini matematiksel olarak gösterdi ve rezonans frekansını türetti. İngiliz radyo araştırmacısı Oliver Lodge , büyük bir Leyden kavanoz pilini uzun bir tel aracılığıyla boşaltarak, ses aralığındaki rezonans frekansıyla, boşaldığında kıvılcımdan müzikal bir ton üreten bir akort devresi oluşturdu. 1857'de Alman fizikçi Berend Wilhelm Feddersen , dönen bir aynada rezonanslı bir Leyden kavanoz devresi tarafından üretilen kıvılcımı fotoğrafladı ve salınımların görünür kanıtını sağladı. 1868'de İskoç fizikçi James Clerk Maxwell , endüktans ve kapasitanslı bir devreye alternatif akım uygulamanın etkisini hesapladı ve tepkinin rezonans frekansında maksimum olduğunu gösterdi. Bir elektrik rezonans eğrisinin ilk örneği, 1887'de Alman fizikçi Heinrich Hertz tarafından radyo dalgalarının keşfi üzerine öncü makalesinde yayınlandı ve kıvılcım aralığı LC rezonatör dedektörlerinden elde edilebilen kıvılcım uzunluğunu frekansın bir fonksiyonu olarak gösterdi.
Ayarlanmış devreler arasındaki rezonansın ilk gösterimlerinden biri, 1889 civarında Lodge'un "syntonik kavanozlar" deneyiydi. Her biri, bir kıvılcım aralığı olan ayarlanabilir tek dönüşlü bir bobine bağlı bir Leyden kavanozundan oluşan iki rezonans devresini yan yana yerleştirdi. Bir ayarlı devreye bir endüksiyon bobininden yüksek bir voltaj uygulandığında, kıvılcımlar ve dolayısıyla salınımlı akımlar meydana geldiğinde, diğer ayarlı devrede kıvılcımlar sadece devreler rezonansa ayarlandığında uyarıldı. Lodge ve bazı İngiliz bilim adamları bu etki için " sintoni " terimini tercih ettiler , ancak " rezonans " terimi sonunda kaldı. LC devreleri için ilk pratik kullanım , alıcı ve vericinin aynı frekansa ayarlanmasını sağlamak için 1890'larda kıvılcım aralığı radyo vericilerindeydi . İlk pratik sistemler 1900'de İtalyan radyo öncüsü Guglielmo Marconi tarafından icat edilmesine rağmen, ayarlamaya izin veren bir radyo sistemi için ilk patent 1897'de Lodge tarafından dosyalandı .
Ayrıca bakınız
Referanslar
Dış bağlantılar
- Tony Kuphaldt'ın elektrikli sarkaç , LC tankının çalışması hakkında klasik bir hikaye.
- Paralel-LC devresinin enerjiyi nasıl depoladığı başka bir mükemmel LC kaynağıdır.












































![{\displaystyle {\mathcal {L}}\left[f(t)\right]={\mathcal {L}}\left[{\frac {\mathrm {d} ^{2}v}{\mathrm { d} t^{2}}}+\omega _{0}^{2}v\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30cbcf2f1819cc4f603a0a2ad3a45811b97fc4e4)


![{\displaystyle v(t)=v_{0}\cos(\omega _{0}t)+{\frac {v'_{0}}{\omega _{0}}}\sin(\omega _ {0}t)+{\mathcal {L}}^{-1}\left[{\frac {F(s)}{s^{2}+\omega _{0}^{2}}}\ sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45c285c8ecf64f776538ac642c546731c90298f4)

![{\displaystyle {\mathcal {L}}^{-1}\left[\omega _{0}^{2}{\frac {V_{in}(s)}{s^{2}+\omega _ {0}^{2}}}\right]={\mathcal {L}}^{-1}\left[\omega _{0}^{2}M{\frac {1}{s^ {2}+\omega _{0}^{2})}\sağ]=M(1-\cos(\omega _{0}t))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef60af8194e4e7c94c43a8f36e04b4f0899d889f)


![{\displaystyle {\mathcal {L}}^{-1}\left[\omega _{0}^{2}{\frac {1}{s^{2}+\omega _{0}^{2 }}}{\frac {U\omega _{f}}{s^{2}+\omega _{f}^{2}}}\right]={\mathcal {L}}^{-1} \left[{\frac {\omega _{0}^{2}U\omega _{f}}{\omega _{f}^{2}-\omega _{0}^{2}}}\ sol({\frac {1}{s^{2}+\omega _{0}^{2}}}-{\frac {1}{s^{2}+\omega _{f}^{2 }}}\right)\right]={\frac {\omega _{0}^{2}U\omega _{f}}{\omega _{f}^{2}-\omega _{0} ^{2}}}\left({\frac {1}{\omega _{0}}}\sin(\omega _{0}t)-{\frac {1}{\omega _{f}} }\sin(\omega _{f}t)\sağ)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8a9fa8b4b72855ce52a23d207d1e1891ed54cb)
