Geometrik optik - Geometrical optics

Geometrik optik veya ışın optiği , ışığın yayılmasını ışınlar cinsinden tanımlayan bir optik modelidir . Geometrik optikteki ışın, ışığın belirli koşullar altında yayıldığı yolları tahmin etmek için yararlı bir soyutlamadır .

Geometrik optiğin basitleştirici varsayımları, ışık ışınlarını içerir:

• homojen bir ortamda seyahat ederken düz çizgi yollarında yayılırlar.
• bükülebilir ve özel durumlarda iki farklı ortam arasındaki arayüzde ikiye bölünebilir
• kırılma indisinin değiştiği bir ortamda eğri yolları takip edin
• emilebilir veya yansıtılabilir.

Geometrik optik, kırınım ve girişim gibi belirli optik etkileri hesaba katmaz . Bu sadeleştirme pratikte yararlıdır; dalga boyu, ışığın etkileştiği yapıların boyutuna kıyasla küçük olduğunda mükemmel bir yaklaşımdır. Teknikler, optik sapmalar da dahil olmak üzere , görüntülemenin geometrik yönlerini tanımlamada özellikle yararlıdır .

Açıklama

Uzayda ışık seyahatleri gibi, salınımı içinde genliği . Bu görüntüde, her bir maksimum genlik tepesi , dalga cephesini göstermek için bir düzlemle işaretlenmiştir . Ray oktur dik Bunlara paralel yüzeyler.

Bir ışık ışını a, çizgi veya eğri bir dik ışığın için dalga cephelerinin (ve bu nedenle eşdoğrusal ile dalga vektörü ). Bir ışık ışını için biraz daha kesin bir tanım, bir ışık ışını tarafından iki nokta arasında alınan yolun, en kısa sürede geçilebilecek yol olduğunu belirten Fermat ilkesinden gelir .

Geometrik optikler genellikle eksen dışı yaklaşım veya "küçük açı yaklaşımı" yapılarak basitleştirilir . Matematiksel davranış daha sonra doğrusal hale gelir ve optik bileşenlerin ve sistemlerin basit matrislerle tanımlanmasına izin verir. Bu , yaklaşık görüntü ve nesne konumları ve büyütmeler gibi optik sistemlerin temel özelliklerini bulmak için kullanılan Gauss optik ve paraksiyal ışın izleme tekniklerine yol açar .

Refleks

Aynasal yansıma diyagramı

Aynalar gibi parlak yüzeyler ışığı basit ve öngörülebilir bir şekilde yansıtır. Bu, uzayda gerçek ( gerçek ) veya tahmin edilmiş ( sanal ) bir konumla ilişkilendirilebilen yansıyan görüntülerin üretilmesine izin verir .

Bu tür yüzeylerde, yansıyan ışının yönü, gelen ışının yüzey normali ile yaptığı açı , ışının çarptığı noktada yüzeye dik bir çizgi ile belirlenir. Gelen ve yansıyan ışınlar tek bir düzlemde bulunur ve yansıyan ışın ile yüzey normali arasındaki açı, gelen ışın ile normal arasındaki açıyla aynıdır. Bu, Yansıma Yasası olarak bilinir .

İçin düz aynalar , yansıma yasası nesnelerin görüntüleri dik ve nesneleri olarak aynanın arkasında aynı mesafe aynanın önünde olduğunu ima eder. Görüntü boyutu, nesne boyutuyla aynıdır. ( Büyütme düz ayna birine eşittir.) Yasa ayrıca ima ayna görüntüleri olan ters paritesi bir sol-sağ inversiyon gibi algılanmaktadır.

Kavisli yüzeylere sahip aynalar, ışın izleme ve yüzeydeki her noktada yansıma yasası kullanılarak modellenebilir . İçin parabolik yüzeyler ile ayna , bir ayna üretmek paralel ışınlarının, ortak bir yakınsama ışınları yansıyan odak . Diğer kavisli yüzeyler de ışığı odaklayabilir, ancak farklı şekillerden kaynaklanan sapmalar, odağın uzayda dağılmasına neden olur. Özellikle, küresel aynalar küresel sapma sergiler . Eğri aynalar, birden fazla veya daha az büyütme ile görüntüler oluşturabilir ve görüntü dik veya ters olabilir. Aynadaki yansımayla oluşan dik bir görüntü her zaman sanaldır, tersine çevrilmiş bir görüntü ise gerçektir ve bir ekrana yansıtılabilir.

Refraksiyon

Snell Yasasının İllüstrasyonu

Işık, değişen kırılma indisine sahip bir uzay alanından geçtiğinde kırılma meydana gelir. En basit kırılma durumu, kırılma indisine sahip düzgün bir ortam ile kırılma indisine sahip başka bir ortam arasında bir arayüz olduğunda meydana gelir . Bu gibi durumlarda, Snell Yasası , ışık ışınının ortaya çıkan sapmasını tanımlar: ${\görüntüleme stili n_{1}}$${\ Displaystyle n_{2}}$

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\ }$

burada ve sırasıyla normal (arayüze) ve gelen ve kırılan dalgalar arasındaki açılardır. Bu fenomen, aynı zamanda, yukarıda verilen kırılma indisi tanımından da görüldüğü gibi, değişen ışık hızıyla da ilişkilidir: ${\görüntüleme stili\teta _{1}}$${\ Displaystyle \ theta _{2}}$

${\displaystyle v_{1}\sin \theta _{2}\ =v_{2}\sin \theta _{1}}$

nerede ve ilgili ortamdaki dalga hızları. ${\displaystyle v_{1}}$${\displaystyle v_{2}}$

Snell Yasasının çeşitli sonuçları arasında, yüksek kırılma indeksli bir malzemeden düşük kırılma indeksli bir malzemeye geçen ışık ışınları için, arayüz ile etkileşimin sıfır iletimle sonuçlanmasının mümkün olduğu gerçeği yer alır. Bu fenomene toplam iç yansıma denir ve fiber optik teknolojisine izin verir . Işık sinyalleri bir fiber optik kablodan geçerken, kablo uzunluğu boyunca esasen hiçbir ışık kaybına izin vermeyen toplam iç yansımaya uğrarlar. Yansıma ve kırılma kombinasyonunu kullanarak polarize ışık ışınları üretmek de mümkündür : Kırılan bir ışın ve yansıyan ışın bir dik açı oluşturduğunda , yansıyan ışın "düzlem polarizasyonu" özelliğine sahiptir. Böyle bir senaryo için gereken geliş açısı Brewster açısı olarak bilinir .

Snell Yasası, kırılma indeksleri ve ortamın geometrisi bilindiği sürece, ışık ışınlarının "doğrusal ortamdan" geçerken sapmasını tahmin etmek için kullanılabilir. Örneğin, ışığın bir prizmadan yayılması, prizmanın şekline ve yönüne bağlı olarak ışık ışınının sapmasına neden olur. Ek olarak, ışığın farklı frekansları çoğu malzemede biraz farklı kırılma indekslerine sahip olduğundan, kırılma, gökkuşağı gibi görünen dağılım spektrumları üretmek için kullanılabilir . Işığı prizmadan geçirirken bu fenomenin keşfi ünlü olarak Isaac Newton'a atfedilir .

Bazı ortamların, konuma göre kademeli olarak değişen bir kırılma indisi vardır ve bu nedenle, ışık ışınları düz çizgilerde ilerlemek yerine ortam boyunca kıvrılır. Bu etki, havanın değişen kırılma indisinin ışık ışınlarının bükülmesine neden olduğu ve uzakta (bir su havuzunun yüzeyindeymiş gibi) aynasal yansımaların görünümüne neden olduğu sıcak günlerde görülen seraplardan sorumludur . Değişken bir kırılma indeksine sahip malzemeye gradyan indeksli (GRIN) malzeme denir ve fotokopi makineleri ve tarayıcılar dahil olmak üzere modern optik tarama teknolojilerinde kullanılan birçok faydalı özelliğe sahiptir . Bu fenomen, gradyan indeksli optikler alanında incelenmiştir .

Basit bir yakınsak mercek için bir ışın izleme diyagramı.

Kırılma nedeniyle birleşen veya uzaklaşan ışık ışınları üreten bir cihaza mercek denir . İnce lensler, her iki tarafta da lens üreticisi denklemi kullanılarak modellenebilen odak noktaları üretir . Genel olarak iki tür mercek vardır: paralel ışık ışınlarının yakınsamasına neden olan dışbükey mercekler ve paralel ışık ışınlarının uzaklaşmasına neden olan içbükey mercekler . Bu lensler tarafından görüntülerin nasıl üretildiğinin ayrıntılı tahmini, kavisli aynalara benzer şekilde ışın izleme kullanılarak yapılabilir. Kavisli aynalara benzer şekilde, ince lensler belirli bir odak uzaklığı ( ) ve nesne mesafesi ( ) verilen görüntülerin konumunu belirleyen basit bir denklemi takip eder : ${\görüntüleme stili f}$${\ Displaystyle S_{1}}$

${\displaystyle {\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}}$

nerede görüntü ile ilişkili ve merceğin nesne ile aynı tarafında ise negatif ve merceğin karşı tarafında ise pozitif olarak kabul edilen ve geleneksel olarak kabul edilen mesafedir. Odak uzaklığı f, içbükey mercekler için negatif olarak kabul edilir. ${\ Displaystyle S_{2}}$

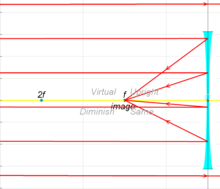
Gelen paralel ışınlar, dışbükey bir mercek tarafından, merceğin uzak tarafında, mercekten bir odak uzaklığı olan ters çevrilmiş gerçek bir görüntüye odaklanır.

Gelen paralel ışınlar, dışbükey bir mercek tarafından, merceğin uzak tarafında, mercekten bir odak uzaklığında, ters çevrilmiş gerçek bir görüntüye odaklanır.

Sonlu mesafedeki bir nesneden gelen ışınlar, odak mesafesinden ziyade mercekten daha uzağa odaklanır; cisim merceğe ne kadar yakınsa, görüntü mercekten o kadar uzaktır. İçbükey merceklerde, gelen paralel ışınlar merceğin içinden geçtikten sonra, merceğin paralel ışınların yaklaştığı merceğin aynı tarafında, merceğin bir odak uzaklığında dik bir sanal görüntüden kaynaklanmış gibi görünecek şekilde birbirinden uzaklaşır. .

İçbükey merceklerde, gelen paralel ışınlar merceğin içinden geçtikten sonra, merceğin paralel ışınların yaklaştığı merceğin aynı tarafında, merceğin bir odak uzaklığında dik bir sanal görüntüden kaynaklanmış gibi görünecek şekilde birbirinden uzaklaşır. .

Sonlu mesafedeki bir nesneden gelen ışınlar, merceğe odak uzunluğundan daha yakın olan ve merceğin nesneyle aynı tarafında bulunan sanal bir görüntü ile ilişkilendirilir. Nesne merceğe ne kadar yakınsa, sanal görüntü merceğe o kadar yakındır.

Sonlu mesafedeki bir nesneden gelen ışınlar, merceğe odak uzunluğundan daha yakın olan ve merceğin nesneyle aynı tarafında bulunan sanal bir görüntü ile ilişkilendirilir.

Aynı şekilde, bir merceğin büyütmesi şu şekilde verilir:

${\displaystyle M=-{\frac {S_{2}}{S_{1}}}={\frac {f}{f-S_{1}}}}$

burada negatif işaret, geleneksel olarak, pozitif değerler için dik bir nesneyi ve negatif değerler için ters çevrilmiş bir nesneyi belirtmek için verilir. Aynalara benzer şekilde, tek lensler tarafından üretilen dik görüntüler sanal, ters çevrilmiş görüntüler ise gerçektir.

Lensler, görüntüleri ve odak noktalarını bozan sapmalardan muzdariptir . Bunlar hem geometrik kusurlardan hem de ışığın farklı dalga boyları için değişen kırılma indeksinden ( kromatik sapma ) kaynaklanmaktadır.

Temel matematik

Matematiksel bir çalışma olarak geometrik optik , hiperbolik kısmi diferansiyel denklemlerin çözümleri için kısa dalga boyu limiti (Sommerfeld-Runge yöntemi) veya Maxwell denklemlerine göre (Luneburg yöntemi) alan süreksizliklerinin yayılmasının bir özelliği olarak ortaya çıkar. Bu kısa dalga boyu limitinde, çözümü yerel olarak şu şekilde tahmin etmek mümkündür:

${\displaystyle u(t,x)\yaklaşık a(t,x)e^{i(k\cdot x-\omega t)}}$

Burada bir dağılım ilişkisi sağlanır ve genlik yavaş değişir. Daha doğrusu, önde gelen sipariş çözümü şu şekli alır: ${\görüntüleme stili k,\omega }$${\görüntüleme stili a(t,x)}$

${\displaystyle a_{0}(t,x)e^{i\varphi (t,x)/\varepsilon }.}$

Faz , büyük dalga sayısını ve frekansı kurtarmak için doğrusallaştırılabilir . Genlik bir taşıma denklemini karşılar . Küçük parametre , yüksek salınımlı başlangıç ​​koşulları nedeniyle sahneye girer. Bu nedenle, başlangıç ​​koşulları diferansiyel denklemin katsayılarından çok daha hızlı salındığında, çözümler oldukça salınımlı olacak ve ışınlar boyunca taşınacaktır. Diferansiyel denklemdeki katsayıların düzgün olduğunu varsayarsak, ışınlar da düzgün olacaktır. Başka bir deyişle, kırılma gerçekleşmez. Bu tekniğin motivasyonu, kısa dalga boyundaki ışığın, seyahat süresini (az ya da çok) en aza indiren ışınlar boyunca hareket ettiği tipik ışık yayılımı senaryosunu incelemekten gelir. Tam uygulaması, mikro yerel analiz araçları gerektirir . ${\displaystyle \varphi (t,x)/\varepsilon }$${\displaystyle k:=\nabla _{x}\varphi }$${\displaystyle \omega :=-\partial _{t}\varphi }$${\displaystyle a_{0}}$${\ Displaystyle \ varepsilon \,}$

Sommerfeld–Runge yöntemi

Sıfır dalga boyunun sınırını alarak geometrik optik denklemlerini elde etme yöntemi ilk olarak 1911'de Arnold Sommerfeld ve J. Runge tarafından tanımlanmıştır . Bunların türetilmesi Peter Debye'nin sözlü bir yorumuna dayanmaktadır . Monokromatik skalar alanı göz önünde , burada bileşenlerin herhangi biri olabilir , elektrik ya da manyetik alan ve dolayısıyla fonksiyonu dalga denklemini karşılamak ${\displaystyle \psi (\mathbf {r} ,t)=\phi (\mathbf {r} )e^{i\omega t}}$${\görüntüleme stili\psi }$${\görüntüleme stili\phi }$

${\displaystyle \nabla ^{2}\phi +k_{o}^{2}n(\mathbf {r} )\phi =0}$

burada ile olmak ışığın hızı vakumla. Burada ise kırılma indisi orta. Genelliği kaybetmeden , denklemi şuna dönüştürmeye girişelim: ${\displaystyle k_{o}=\omega /c=2\pi /\lambda _{o}}$${\görüntüleme stili c}$${\displaystyle n(\mathbf {r} )}$${\displaystyle \phi =A(k_{o},\mathbf {r} )e^{ik_{o}S(\mathbf {r} )}}$

${\displaystyle -k_{o}^{2}A[(\nabla S)^{2}-n^{2}]+2ik_{o}(\nabla S\cdot \nabla A)+ik_{o} A\nabla ^{2}S+\nabla ^{2}A=0.}$

Geometrik optiğin altında yatan ilke limitte yattığından , aşağıdaki asimptotik seri varsayılır, ${\displaystyle \lambda _{o}\sim k_{o}^{-1}\rightarrow 0}$

${\displaystyle A(k_{o},\mathbf {r} )=\sum _{m=0}^{\infty }{\frac {A_{m}(\mathbf {r} )}{(ik_{ o})^{m}}}}$

'nin büyük fakat sonlu değeri için , seri ıraksar ve sadece ilk birkaç terimi uygun tutarken dikkatli olunmalıdır. 'nin her değeri için , tutulacak optimum terim sayısı bulunabilir ve optimum sayıdan daha fazla terim eklemek, daha zayıf bir yaklaşımla sonuçlanabilir. Seriyi denklemde yerine koymak ve farklı derecelerdeki terimleri toplamak, ${\görüntüleme stili k_{o}}$${\görüntüleme stili k_{o}}$

${\displaystyle {\begin{aligned}O(k_{o}^{2}):&\quad (\nabla S)^{2}=n^{2},\\O(k_{o}): &\quad 2\nabla S\cdot \nabla A_{0}+A_{0}\nabla ^{2}S=0,\\O(1):&\quad 2\nabla S\cdot \nabla A_{ 1}+A_{1}\nabla ^{2}S=-\nabla ^{2}A_{0},\end{aligned}}}$

Genel olarak,

${\displaystyle O(k_{o}^{1-m}):\quad 2\nabla S\cdot \nabla A_{m}+A_{m}\nabla ^{2}S=-\nabla ^{2 }A_{m-1}.}$

Birinci denklem olarak bilinen eikonal denklem belirler eikonal a, Hamilton-Jacobi denklemi Kartezyen koordinatlarında, örneğin yazılmış olur, ${\ Displaystyle S(\mathbf {r} )}$

${\displaystyle \sol({\frac {\partial S}{\partial x}}\sağ)^{2}+\left({\frac {\partial S}{\partial y}}\sağ)^{ 2}+\sol({\frac {\partial S}{\partial z}}\sağ)^{2}=n^{2}.}$

Kalan denklemler fonksiyonları belirler . ${\ Displaystyle A_{m}(\mathbf {r} )}$

Lüneburg yöntemi

Maxwell denklemlerinin süreksizliklerinin yüzeylerini analiz ederek geometrik optik denklemlerini elde etme yöntemi ilk olarak 1944'te Rudolf Karl Luneburg tarafından tanımlanmıştır . Elektromanyetik alanın özel bir forma sahip olmasını kısıtlamaz (Sommerfeld-Runge yönteminde değildir genliği bağımlı hale getirilen bir alanın yine de eikonal denklemi, yani bir geometrik optik dalga cephesini vereceğinden emin olun). Bu yaklaşımın ana sonucu şudur: ${\görüntüleme stili\phi }$${\ Displaystyle \ omega }$

Teorem. Alanların ve (dielektrik sabitleri ve ile tanımlanan lineer bir izotropik ortamda ) denklemiyle açıklanan (hareket eden) bir yüzey boyunca sonlu süreksizliklere sahip olduğunu varsayalım . O zaman, integral formdaki Maxwell denklemleri , eikonal denklemi sağladığını ima eder : ${\displaystyle \mathbf {\vec {E}} (x,y,z,t)}$${\displaystyle \mathbf {\vec {H}} (x,y,z,t)}$${\görüntüleme stili \varepsilon (x,y,z)}$${\görüntüleme stili \mu (x,y,z)}$${\displaystyle \mathbf {R} ^{3}}$${\görüntüleme stili \psi (x,y,z)-ct=0}$${\görüntüleme stili\psi }$

${\displaystyle \psi _{x}^{2}+\psi _{y}^{2}+\psi _{z}^{2}=\varepsilon \mu =n^{2}}$,

ortamın kırılma indisi nerede (Gauss birimleri). ${\görüntüleme stili n}$

Böyle bir süreksizlik yüzeyine bir örnek, belirli bir zamanda yayılmaya başlayan bir kaynaktan yayılan ilk dalga cephesidir.

Alan süreksizliğinin yüzeyleri böylece, aşağıdaki şekilde tanımlanan karşılık gelen geometrik optik alanlar ile geometrik optik dalga cepheleri haline gelir:

${\displaystyle \mathbf {\vec {E}} ^{*}(x,y,z)=\mathbf {\vec {E}} (x,y,z,\psi (x,y,z)/ C)}$

${\displaystyle \mathbf {\vec {H}} ^{*}(x,y,z)=\mathbf {\vec {H}} (x,y,z,\psi (x,y,z)/ C)}$

Bu alanlar, Sommerfeld-Runge yaklaşımının taşıma denklemleriyle tutarlı olan taşıma denklemlerine uyar. Luneburg'un teorisindeki ışık ışınları, süreksizlik yüzeylerine dik yörüngeler olarak tanımlanır ve doğru parametrelendirme ile Fermat'ın en az zaman ilkesine uydukları gösterilebilir, böylece bu ışınların standart optik ışık ışınlarıyla özdeşliği kurulabilir.

Yukarıdaki gelişmeler anizotropik ortama genelleştirilebilir.

Luneburg teoreminin ispatı, Maxwell denklemlerinin çözümlerin süreksizliklerinin yayılmasını nasıl yönettiğini araştırmaya dayanır. Temel teknik lemma aşağıdaki gibidir:

Teknik bir lemma. Izin uzay zamanda hiperyüzeyi (3-boyutlu bir manifold) olabilir : bir ya da daha fazla üzerinde , , , , sonlu bir süreksizlik vardır. Daha sonra hiper yüzeyin her noktasında aşağıdaki formüller geçerlidir: ${\displaystyle \varphi (x,y,z,t)=0}$${\displaystyle \mathbf {R} ^{4}}$${\displaystyle \mathbf {\vec {E}} (x,y,z,t)}$${\displaystyle \mathbf {\vec {H}} (x,y,z,t)}$${\görüntüleme stili \varepsilon (x,y,z)}$${\görüntüleme stili \mu (x,y,z)}$

${\displaystyle \nabla \varphi \times [\mathbf {\vec {H}} ]-{1 \over c}\,\varphi _{t}\,[\varepsilon \mathbf {\vec {E}} ] =0}$

${\displaystyle \nabla \varphi \times [\mathbf {\vec {E}} ]+{1 \over c}\,\varphi _{t}\,[\mu \mathbf {\vec {H}} ] =0}$

${\displaystyle \nabla \cdot [\varepsilon \mathbf {\vec {E}} ]=0}$

${\displaystyle \nabla \cdot [\mu \mathbf {\vec {H}} ]=0}$

burada operatör hareket ile uzay (her sabit için ) ve köşeli parantezler süreksizlik yüzeyinin her iki tarafında değerlerindeki fark (kurmak rasgele bir göre, fakat kuralı sabit örneğin gradyan ifade miktarlarda yönünde işaret ' den çıkarılır ). ${\görüntüleme stili\nabla }$${\görüntüleme stili xyz}$${\görüntüleme stili t}$${\displaystyle \nabla \varphi }$

Kanıt taslağı. Kaynaklardan uzakta Maxwell denklemleriyle başlayın (Gauss birimleri):

${\displaystyle \nabla \cdot \varepsilon \mathbf {\vec {E}} =0}$

${\displaystyle \nabla \cdot \mu \mathbf {\vec {H}} =0}$

${\displaystyle \nabla \times \mathbf {\vec {E}} +{\mu \overc}\,\mathbf {\vec {H}} _{t}=0}$

${\displaystyle \nabla \times \mathbf {\vec {H}} -{\varepsilon \over c}\,\mathbf {\vec {E}} _{t}=0}$

İçinde Stokes teoremini kullanarak bir herhangi bir alan için yukarıdaki denklemlerin birinci gelen sonuca varabiliriz içinde bir çıkaran parça parça ile sınır pürüzsüz şu doğrudur: ${\displaystyle \mathbf {R} ^{4}}$${\görüntüleme stili D}$${\displaystyle \mathbf {R} ^{4}}$${\görüntüleme stili \Gama }$

${\displaystyle \oint _{\Gamma }(\mathbf {\vec {M}} \cdot \varepsilon \mathbf {\vec {E}} )\,dS=0}$

burada , normal olarak dışarı doğru birimin projeksiyonu ve 3D dilime ve ses seviyesi 3-formudur . Benzer şekilde, kalan Maxwell denklemlerinden aşağıdakiler belirlenir: ${\displaystyle \mathbf {\vec {M}} =(x_{N},y_{N},z_{N})}$${\displaystyle (x_{N},y_{N},z_{N},t_{N})}$${\görüntüleme stili \Gama }$${\displaystyle t={\rm {const}}}$${\görüntüleme stili dS}$${\görüntüleme stili \Gama }$

${\displaystyle \oint _{\Gamma }(\mathbf {\vec {M}} \cdot \mu \mathbf {\vec {H}} )\,dS=0}$

${\displaystyle \oint _{\Gamma }(\mathbf {\vec {M}} \times \mathbf {\vec {E}} +{\mu \over c}\,t_{N}\,\mathbf { \vec {H}} )\,dS=0}$

${\displaystyle \oint _{\Gamma }(\mathbf {\vec {M}} \times \mathbf {\vec {H}} -{\varepsilon \over c}\,t_{N}\,\mathbf { \vec {E}} )\,dS=0}$

Şimdi keyfi bir alt yüzeyleri dikkate alınarak arasında ve çevredeki küçük mahalle kurma olarak , bir elde eder ve buna uygun olarak yukarıda belirtilen integralleri çıkarılması: ${\görüntüleme stili \Gama _{0}}$${\görüntüleme stili \Gama }$${\görüntüleme stili \Gama _{0}}$${\displaystyle \mathbf {R} ^{4}}$

${\displaystyle \int _{\Gamma _{0}}(\nabla \varphi \cdot [\varepsilon \mathbf {\vec {E}} ])\,{dS \over \|\nabla ^{4D}\ varphi \|}=0}$

${\displaystyle \int _{\Gamma _{0}}(\nabla \varphi \cdot [\mu \mathbf {\vec {H}} ])\,{dS \over \|\nabla ^{4D}\ varphi \|}=0}$

${\displaystyle \int _{\Gamma _{0}}\left(\nabla \varphi \times [\mathbf {\vec {H}} ]-{1 \over c}\,\varphi _{t}\ ,[\varepsilon \mathbf {\vec {E}} ]\sağ)\,{dS \over \|\nabla ^{4D}\varphi \|}=0}$

${\displaystyle \int _{\Gamma _{0}}\left(\nabla \varphi \times [\mathbf {\vec {E}} ]+{1 \over c}\,\varphi _{t}\ ,[\mu \mathbf {\vec {H}} ]\sağ)\,{dS \over \|\nabla ^{4D}\varphi \|}=0}$

burada 4B uzayındaki gradyanı belirtir . Ve keyfi olduğu için, integrallerin 0'a eşit olması gerekir, bu da lemmayı ispatlar. ${\görüntüleme stili \nabla ^{4D}}$${\ Displaystyle xyzt}$${\görüntüleme stili \Gama _{0}}$

Sürekli bir ortamda yayılırken süreksizlik yüzeylerinin eikonal denkleme uyduğunu göstermek artık kolay. Spesifik olarak, eğer ve sürekli ise, o zaman süreksizlikler ve aşağıdakileri karşılar: ve . Bu durumda lemmanın ilk iki denklemi şu şekilde yazılabilir: ${\görüntüleme stili\varepsilon }$${\görüntüleme stili \mu }$${\displaystyle \mathbf {\vec {E}} }$${\displaystyle \mathbf {\vec {H}} }$${\displaystyle [\varepsilon \mathbf {\vec {E}} ]=\varepsilon [\mathbf {\vec {E}} ]}$${\displaystyle [\mu \mathbf {\vec {H}} ]=\mu [\mathbf {\vec {H}} ]}$

${\displaystyle \nabla \varphi \times [\mathbf {\vec {H}} ]-{\varepsilon \over c}\,\varphi _{t}\,[\mathbf {\vec {E}} ]= 0}$

${\displaystyle \nabla \varphi \times [\mathbf {\vec {E}} ]+{\mu \over c}\,\varphi _{t}\,[\mathbf {\vec {H}} ]= 0}$

Birinci denklemin çapraz çarpımını ikinci verimle almak ve yerine koymak: ${\displaystyle \nabla \varphi }$

${\displaystyle \nabla \varphi \times (\nabla \varphi \times [\mathbf {\vec {H}} ])-{\varepsilon \over c}\,\varphi _{t}\,(\nabla \ varphi \times [\mathbf {\vec {E}} ])=(\nabla \varphi \cdot [\mathbf {\vec {H}} ])\,\nabla \varphi -\|\nabla \varphi \| ^{2}\,[\mathbf {\vec {H}} ]+{\varepsilon \mu \over c^{2}}\varphi _{t}^{2}\,[\mathbf {\vec { H}} ]=0}$

Maxwell denklemlerinin ikincisine göre , bu nedenle, yalnızca yüzeyde bulunan noktalar için : ${\displaystyle \nabla \varphi \cdot [\mathbf {\vec {H}} ]=0}$${\görüntüleme stili \varphi =0}$

${\displaystyle \|\nabla \varphi \|^{2}={\varepsilon \mu \over c^{2}}\varphi _{t}^{2}}$

(Süreksizliğin varlığının, aksi takdirde sıfıra böleceğimiz için bu adımda çok önemli olduğuna dikkat edin.)

Fiziksel hususlar nedeniyle , aşağıdaki biçimde olan bir genellik kaybı olmaksızın varsayılabilir : yani, düz yüzeyler olarak modellenen, uzayda hareket eden bir 2B yüzey . (Matematiksel eğer var ile örtülü fonksiyon teoremi .) Olarak yukarıda yazılı denklem haline gelir: ${\görüntüleme stili \varphi }$${\displaystyle \varphi (x,y,z,t)=\psi (x,y,z)-ct}$${\görüntüleme stili\psi }$${\görüntüleme stili\psi }$${\displaystyle \varphi _{t}\neq 0}$${\görüntüleme stili\psi }$

${\displaystyle \|\nabla \psi \|^{2}={\varepsilon \mu \over c^{2}}\,(-c)^{2}=\varepsilon \mu =n^{2} }$

yani,

${\displaystyle \psi _{x}^{2}+\psi _{y}^{2}+\psi _{z}^{2}=n^{2}}$

bu eikonal denklemdir ve değişken olmadığı için , , , için geçerlidir . Gibi optik diğer yasalar Snell kanun ve Fresnel formüller benzer kesikliklerin dikkate alınarak elde edilebilir ve . ${\görüntüleme stili x}$${\görüntüleme stili y}$${\görüntüleme stili z}$${\görüntüleme stili t}$${\görüntüleme stili\varepsilon }$${\görüntüleme stili \mu }$

Dört vektör gösterimi kullanan genel denklem

Olarak dört vektör kullanılan notasyon özel görelilik , dalga denklemi yazılabilir

${\displaystyle {\frac {\partial ^{2}\psi }{\partial x_{i}\partial x^{i}}}=0}$

ve ikame yol açar ${\displaystyle \psi =Ae^{iS/\epsilon }}$

${\displaystyle -{\frac {A}{\epsilon ^{2}}}{\frac {\partial S}{\partial x_{i}}}{\frac {\partial S}{\partial x^{ i}}}+{\frac {2i}{\epsilon }}{\frac {\kısmi A}{\kısmi x_{i}}}{\frac {\kısmi S}{\kısmi x^{i}} }+{\frac {iA}{\epsilon }}{\frac {\partial ^{2}S}{\partial x_{i}\partial x^{i}}}+{\frac {\partial ^{ 2}A}{\partial x_{i}\partial x^{i}}}=0.}$

Bu nedenle eikonal denklem tarafından verilir

${\displaystyle {\frac {\partial S}{\partial x_{i}}}{\frac {\partial S}{\partial x^{i}}}=0.}$

Yukarıdaki denklem çözülerek eikonal bulunduğunda, dalga dört-vektörü şu şekilde bulunabilir:

${\displaystyle k_{i}=-{\frac {\kısmi S}{\kısmi x^{i}}}.}$

Ayrıca bakınız

• Hamilton optiği
• geometrik akustik

Referanslar

daha fazla okuma

• Robert Alfred Herman (1900) Geometrik optik üzerine Bir İnceleme dan Archive.org .
• "Gözlerin Işığı ve Aydınlanmış Görüş Manzarası" , 16. yüzyıldan kalma geometrik optik hakkında Arapça bir el yazmasıdır.
• Işın Sistemleri Teorisi – İrlanda Kraliyet Akademisi İşlemlerinde WR Hamilton , Cilt. XV, 1828.

Bazı erken kitap ve makalelerin İngilizce çevirileri

• H. Bruns, "Das Eikonal"
• M. Malus, "Optik"
• J. Plucker, "Işık dalgaları için genel formun tartışılması"
• E. Kummer, "Doğrusal ışın sistemlerinin genel teorisi"
• E. Kummer, optik olarak gerçekleştirilebilir doğrusal ışın sistemleri üzerine sunum
• R. Meibauer, "Işık ışınlarının doğrusal sistemleri teorisi"
• M. Pasch, "Işın sistemlerinin odak yüzeyleri ve komplekslerin tekillik yüzeyleri üzerine"
• A. Levistal, "Geometrik optikte araştırma"
• F. Klein, "Bruns eikonal Üzerine"
• R. Dontot, "Entegral değişmezler ve geometrik optiğin bazı noktaları hakkında"
• T. de Donder, "Optiklerin integral değişmezleri üzerine"

Dış bağlantılar

• Fotonik Temelleri – Temel Geometrik Optik Modülü
• Feynman'ın Geometrik Optik üzerine dersi