üs - Exponentiation
| Aritmetik işlemler | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Üs bir olan matematiksel işlem olarak yazılı b n , iki sayıyı içeren baz b ve üs veya güç n ve "olarak telaffuz b kuvvetine yükseltilen n ". Zaman , n pozitif bir tamsayıdır , tekrar için üs alma karşılık çarpma şöyledir: baz b N olan ürün çarpılması N bazlar
Üs genellikle tabanın sağında bir üst simge olarak gösterilir . Bu durumda, içinde b n "denir b yükseltildi n inci güç", " b gücüne yükseltilmiş n ", " n th güç b " " b için n inci güç", ya da çoğu kısaca olarak " b ile n th".
Bir yer alır b 1 = b , ve herhangi bir pozitif tamsayı için m ve n , tek bir sahiptir b n ⋅ b m = b , n + m . Olmayan pozitif tam üs Bu özellik uzatmak için b 0 olarak tanımlanır 1 ve B - n ile ( n pozitif tam sayı ve b sıfır) gibi tanımlanmıştır1/b , n. Özellikle, b -1 eşittir1/B, Karşılıklı ve b .
Üs tanımı, herhangi bir gerçek veya karmaşık üsse izin verecek şekilde genişletilebilir . Tamsayı üsleriyle üs alma, matrisler de dahil olmak üzere çok çeşitli cebirsel yapılar için de tanımlanabilir .
Üs alma, bileşik faiz , nüfus artışı , kimyasal reaksiyon kinetiği , dalga davranışı ve açık anahtarlı şifreleme gibi uygulamalarla ekonomi , biyoloji , kimya , fizik ve bilgisayar bilimi dahil olmak üzere birçok alanda yaygın olarak kullanılmaktadır .
Notasyonun tarihi
Güç terimi ( Latince : potentia, potestas, dignitas ), Yunan matematikçi Euclid tarafından Sakızlı Hipokrat'tan sonra bir çizginin karesi için kullanılan antik Yunanca δύναμις ( dúnamis , burada: "büyütme") kelimesinin yanlış tercümesidir . Gelen Kum Hesap görücü , Arşimet keşfetti ve üstlerin hukuku, kanıtladı 10 bir ⋅ 10 b = 10 a + b yetkilerini işlemek için gerekli 10 . 9. yüzyılda, İranlı matematikçi Muhammed ibn Mūsā al-Khwārizmī bir kare için مَال ( māl , "mülk", "mülk") terimlerini kullandı - Müslümanlar, "o ve önceki zamanların çoğu matematikçisi gibi, bir kareyi düşündüler. bir alanın, özellikle toprağın, dolayısıyla mülkün bir tasviri olarak sayı" - ve daha sonra İslam matematikçilerinin matematiksel gösterimde mīm (m) ve kāf (k) harfleri olarak temsil ettiği bir küp için كَعْبَة ( ka'bah , "küp" ), sırasıyla 15. yüzyıla kadar, Abū al-Hasan ibn Ali al-Qalasādi'nin eserinde görüldüğü gibi .
16. yüzyılın sonlarında Jost Bürgi , üsler için Roma rakamlarını kullandı.
Nicolas Chuquet , 15. yüzyılda, daha sonra Henricus Grammateus ve Michael Stifel tarafından 16. yüzyılda kullanılan bir üstel gösterim biçimi kullandı . Üs kelimesi 1544'te Michael Stifel tarafından icat edildi. 1696'da Samuel Jeake endeks terimini tanıttı. 16. yüzyılda, Robert Recorde kare, küp, zenzizenzic ( dördüncü kuvvet ), sursolid (beşinci), zenzicube (altıncı), ikinci sursolid (yedinci) ve zenzizenzizenzic (sekizinci) terimlerini kullandı. . Biquadrate , dördüncü güce atıfta bulunmak için de kullanılmıştır.
17. yüzyılın başlarında, modern üstel gösterimimizin ilk biçimi René Descartes tarafından La Géométrie başlıklı metninde tanıtıldı ; orada, gösterim Kitap I'de tanıtılır.
Bazı matematikçiler ( Isaac Newton gibi ) üsleri yalnızca ikiden büyük kuvvetler için kullandılar ve kareleri tekrarlanan çarpma olarak temsil etmeyi tercih ettiler. Böylece polinomları örneğin ax + bxx + cx 3 + d olarak yazarlardı .
Başka bir tarihsel eşanlamlı olan involution , artık nadirdir ve daha yaygın anlamı ile karıştırılmamalıdır .
1748'de Leonhard Euler , değişken üsleri ve dolaylı olarak tamsayı olmayan üsleri yazarak tanıttı:
"Üssün kendisinin bir değişken olduğu üstelleri veya güçleri düşünün. Bu tür niceliklerin cebirsel fonksiyonlar olmadığı açıktır , çünkü bu türlerde üsler sabit olmalıdır."
terminoloji
Sentezleme b 2 = b ⋅ b "olarak adlandırılan kare arasında b " ya da " B yan uzunluğu olan bir kare alanı için, kare" b olduğunu b 2 .
Aym şekilde, b 3 = b ⋅ b ⋅ b "olarak adlandırılan küp arasında b " ya da " B yan uzunluğu olan bir küp hacmi nedeniyle, küp" b olduğunu b 3 .
Bir olduğunda pozitif tamsayı ; üs tabanının birçok kopya birbiriyle çarpılır nasıl gösterir. Örneğin, 3 5 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243 . Baz 3 belirir 5 üs olduğu için çarpma zamanları 5 . Burada 243 , 3'ün 5. kuvveti veya 5. kuvvetine yükseltilmiş 3'tür .
"Yükseltilmiş" kelimesi genellikle atlanır ve bazen "güç" de kullanılır, bu nedenle 3 5 basitçe "3 üzeri 5" veya "3 üzeri 5" olarak okunabilir. Bu nedenle, üs B n "olarak ifade edilebilir b gücüne n ", " b ile N inci gücü", " b ile n th", ya da "çok kısa bir süre için , b için n ".
İç içe üs ile formül gibi 3 5 7 (yani 3 (5 7 ) olup (3 5 ) 7 ), bir adlandırılır güçlerin kulesi , ya da sadece bir kule .
tamsayı üsleri
Tamsayı üsleriyle üs alma işlemi, doğrudan temel aritmetik işlemlerden tanımlanabilir .
pozitif üsler
Üsün yinelenen bir çarpma olarak tanımı, indüksiyon kullanılarak resmileştirilebilir ve bu tanım, bir ilişkisel çarpım olduğu anda kullanılabilir :
Temel durum
ve nüks olduğu
Çarpmanın birleştirilebilirliği, herhangi bir pozitif tamsayı m ve n için ,
ve
sıfır üs
Tanım olarak, 0 gücüne yükseltilmiş herhangi bir sıfır olmayan sayı 1'dir :
Bu tanım, formülün genişletilmesine izin veren tek olanaktır.
sıfır üslere. Bir özdeşliği olan bir çarpma işlemi ile her cebirsel yapıda kullanılabilir .
Sezgisel olarak, b'nin kopyalarının boş ürünü olarak yorumlanabilir . Yani eşitlik , boş çarpım için genel kuralın özel bir durumudur.
Davası 0 0 daha karmaşıktır. Yalnızca tamsayı güçlerinin dikkate alındığı bağlamlarda , genellikle 1 değerine atanır , aksi takdirde, ona bir değer verilip verilmeyeceği ve hangi değerin atanacağı bağlama bağlı olabilir.
Negatif üsler
Negatif temsilcileri olan Üs herhangi bir tam sayı için de geçerlidir, aşağıdaki kimlik ile tanımlanır , n ve sıfır olmayan , b :
0'ı negatif bir üsse yükseltmek tanımsızdır, ancak bazı durumlarda sonsuz ( ) olarak yorumlanabilir .
Negatif üslerle yapılan bu üs tanımı, özdeşliğin negatif üslere genişletilmesine izin veren tek tanımdır (durumu düşünün ).
Aynı tanım , çarpımsal bir monoiddeki , yani bir cebirsel yapıdaki , bir ilişkisel çarpım ve 1 ile gösterilen bir çarpımsal özdeşliğe sahip (örneğin, belirli bir boyutun kare matrisleri ) ters çevrilebilir öğeler için de geçerlidir . Özellikle, böyle bir yapıda, ters çevrilebilir bir eleman x'in tersi standart olarak gösterilir.
Kimlikler ve özellikler
Aşağıdaki kimlikler , genellikle üs kuralları , tabanın sıfır olmaması koşuluyla tüm tamsayı üsleri için geçerlidir:
Toplama ve çarpmanın aksine, üs alma değişmeli değildir . Örneğin, 2 3 = 8 ≠ 3 2 = 9 . Ayrıca toplama ve çarpmanın aksine, üs alma ilişkisel değildir . Örneğin (2 3 ) 2 = 8 2 = 64 , oysa 2 (3 2 ) = 2 9 = 512 . Parantezler olmadan, üst simge gösteriminde seri üs alma için geleneksel işlem sırası, aşağıdan yukarıya (veya sol - birleştirici ) değil , yukarıdan aşağıya (veya sağ - ilişkiseldir) şeklindedir. Yani,
genel olarak farklı olan
Bir toplamın güçleri
Bir toplamın güçleri normalde toplamların güçlerinden binom formülüyle hesaplanabilir.
Bununla birlikte, bu formül summands gidip halinde geçerlidir (yani, bu ab = ba ) bir aitse ima edilir, yapı olup değişmeli . Aksi takdirde, a ve b örneğin aynı boyutta kare matrislerse , bu formül kullanılamaz. O bu şu bilgisayar cebir , birçok algoritmalar üs alma üsleri gidip olmadığında tamsayı üslerin yer aldığı değiştirilmelidir. Bazı genel amaçlı bilgisayar cebir sistemleri , farklı bir yazım ile (bazen ^^ yerine ^ ) üs daha sonra adı olmayan gidip bazlar ile sigara değişmeli üs .
kombinatoryal yorumlama
Negatif olmayan tamsayılar için , n ve m nin değeri, n, m sayısı fonksiyonları , bir gelen dizi ve m, bir dizi elemanları , n elemanları (bkz ana üs ). Bu tür işlevler, bir n -eleman kümesinden m - tuple'lar (veya n -harfli bir alfabeden m -harfli sözcükler) olarak temsil edilebilir . m ve n'nin belirli değerleri için bazı örnekler aşağıdaki tabloda verilmiştir:
n m N, m, mümkün m kümesinden elemanların -tuples {1, ..., n } 0 5 = 0 Yok 1 4 = 1 (1, 1, 1, 1) 2 3 = 8 (1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2 , 2, 1), (2, 2, 2) 3 2 = 9 (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3 , 3) 4 1 = 4 (1), (2), (3), (4) 5 0 = 1 ()
özel bazlar
on'un güçleri
On tabanlı ( ondalık ) sayı sisteminde, 10'un tamsayı kuvvetleri , üssün işareti ve büyüklüğü ile belirlenen bir dizi sıfırın ardından veya öncesinde 1 rakamı olarak yazılır . Örneğin,10 3 =1000 ve10 -4 =0.0001 .
10 tabanlı üs alma , bilimsel gösterimde büyük veya küçük sayıları belirtmek için kullanılır . Örneğin,299 792 458 m/s ( Işığın boşluktaki hızı, metre/saniye cinsinden ) şu şekilde yazılabilir:2.997 924 58 × 10 8 m/s ve daha sonra yaklaşık olarak2.998 x 10 8 m / sn .
10'un kuvvetlerine dayalı SI önekleri de küçük veya büyük miktarları tanımlamak için kullanılır. Örneğin, ön ek kilo araçları10 3 =1000 yani bir kilometre1000 metre .
iki güç
2'nin ilk negatif güçleri yaygın olarak kullanılır ve özel adlara sahiptir, örneğin: half ve quarter .
Yetkileri 2 görünen küme teorisinin bir dizi beri, n üyeleri bir sahiptir güç seti , onun tüm set alt kümeleri vardır, 2 n üye.
2'nin tamsayı kuvvetleri bilgisayar bilimlerinde önemlidir . 2 n pozitif tamsayı güçleri n - bitlik bir tamsayı ikili sayı için olası değerlerin sayısını verir ; örneğin, bir bayt alabilir 2 8 = 256 farklı değerler. İkili sayı sistemi güçler bir toplamı olarak herhangi bir sayıda ifade 2 ve bir dizi olarak ifade eder , 0 ve 1 ile ayrılmış, ikili noktanın , 1 bir gücünü gösterir 2'de toplam görünür; üs bu 1'in yerine göre belirlenir : negatif olmayan üsler noktanın solundaki ( 0 ' dan başlayarak ) 1'in rankıdır ve negatif üsler noktanın sağındaki rank tarafından belirlenir.
birinin güçleri
Birin kuvvetleri birdir: 1 n = 1 .
Bir sayının ilk kuvveti sayının kendisidir:
sıfırın güçleri
Üs Eğer n, (pozitif olduğu , n > 0 ), n, : sıfır inci güç sıfırdır 0 , n = 0 .
Üs Eğer , n negatif olduğu ( n <0 ), n, sıfır inci güç 0 , n o eşit olmalıdır, çünkü, tanımlanmamış olan - n > 0 , ve bu olur yukarıda göre yöntem.
Sentezleme 0 0 1 ya gibi tanımlanmıştır, ya da sola (tanımlanmamış bakınız Sıfır, sıfır ).
Negatif olanın güçleri
Eğer n, daha sonra tam sayı olduğu (1) , n = 1 .
Eğer n, daha sonra tek bir tam sayı olduğu (1) , n = -1 .
Bu nedenle, -1'in kuvvetleri, değişen dizileri ifade etmek için kullanışlıdır . i karmaşık sayısının kuvvetleriyle ilgili benzer bir tartışma için bkz. § Karmaşık sayıların kuvvetleri .
Büyük üsler
Bir dizinin limiti bir uzaklaşan büyük bir sayı yetkilerinin; başka bir deyişle, dizi sınırsız büyür:
- b n → ∞ as n → ∞ b > 1 olduğunda
Bu şekilde okunabilir " b gücüne n eğilimi için + ∞ olarak N olduğunda sonsuza eğilimi b birden daha büyük olduğu".
Mutlak değeri birden küçük olan bir sayının kuvvetleri sıfır olma eğilimindedir:
- b n → 0 olarak n → ∞ ne zaman | b | < 1
Birinin herhangi bir gücü her zaman birdir:
- b , n = 1 için tüm n ise b = 1
Yetkileri -1 arasında alternatif 1 ve -1 olarak n olarak çift ve tek ve böylece arasında dönüşümlü herhangi sınırı eğilimi yoktur n büyür.
Eğer b < –1 , b n , n çift ve tek arasında değişerek daha büyük ve daha büyük pozitif ve negatif sayılar arasında değişir ve bu nedenle n büyüdükçe herhangi bir sınır eğilimi göstermez .
Üs sonsuzluğa meyilli olduğu için üslü sayı 1'e eğilim gösterirken değişiyorsa , limitin yukarıdakilerden biri olması gerekmez. Özellikle önemli bir durum
- (1 + 1/ n ) n → e as n → ∞
Aşağıdaki § üstel fonksiyona bakın.
Diğer sınırlar, özellikle belirsiz bir biçim alan ifadelerinkiler, aşağıdaki § Yetki sınırları içinde açıklanmıştır .
Güç fonksiyonları
Formun Gerçek fonksiyonları , bazen güç fonksiyonları olarak adlandırılır. Ne zaman bir tamsayı ve , iki birincil aile vardır: çift ve tek için. Genel olarak , ne zaman bile artan ile pozitif sonsuzluğa ve ayrıca azalan ile pozitif sonsuzluğa yönelecektir . Çift güç fonksiyonları ailesinden gelen tüm grafikler, genel şekline sahiptir ve arttıkça ortada daha fazla düzleşir . Bu tür simetriye ( ) sahip işlevlere çift işlevler denir .
Ne zaman garip, 'in asimptotik pozitiften davranış tersine çevirir negatife . Çünkü , aynı zamanda artan ile pozitif sonsuza , azalan ile negatif sonsuza doğru yönelecektir . Tek kuvvet fonksiyonları ailesinden gelen tüm grafikler, genel şekle sahiptir , arttıkça ortada daha fazla düzleşir ve düz çizgide tüm düzlüğünü kaybeder . Bu tür simetriye ( ) sahip işlevlere tek işlevler denir .
için , her durumda zıt asimptotik davranış doğrudur.
Ondalık basamakların güç tablosu
| n | n 2 | n, 3 | n, 4 | n 5 | n 6 | n 7 | n 8 | n 9 | n, 10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 1296 | 7776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7 | 49 | 343 | 2401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
rasyonel üsler
Eğer x , negatif olmayan bir reel sayı ve n pozitif bir tamsayıdır, ya da benzersiz bir pozitif gerçek belirtmektedir , n inci kök bölgesinin x olup, eşsiz pozitif reel sayı y şekildedir
Eğer x pozitif bir reel sayıdır ve a, rasyonel sayı ile, p ve q ≠ 0 tamsayılardır, daha sonra olarak tanımlanmaktadır
Sağdaki eşitlik ayarlanarak ve yazılarak elde edilebilir.
Eğer r , pozitif bir rasyonel sayıdır tanımı gereği.
Bütün bu tanımlar, özdeşliği rasyonel üslere genişletmek için gereklidir .
Öte yandan, bu tanımların pozitif reel sayılar olmayan tabanlara genişletilmesinde sorunlar vardır. Örneğin, negatif reel sayı gerçek vardır n eğer negatif inci kökü, n ise garip ve eğer gerçek kök n bile olduğunu. İkinci durumda, karmaşık hangisi n için inci kök biri seçer kimlik memnun olamaz. Örneğin,
Bu problemlerin nasıl ele alınabileceğine ilişkin ayrıntılar için § Gerçek üsler ve § Karmaşık sayıların güçleri bölümüne bakın .
Gerçek üsler
Pozitif gerçek sayılar için, gerçek güçlere üs alma, ya süreklilik yoluyla rasyonel güçleri gerçeklere genişleterek ( aşağıda § Rasyonel üslerin sınırları ) ya da taban ve üstel fonksiyonun logaritması cinsinden iki eşdeğer şekilde tanımlanabilir. ( § Logaritma yoluyla yetkiler , aşağıda). Sonuç her zaman pozitif bir gerçek sayıdır ve tamsayı üsleri için yukarıda gösterilen özdeşlikler ve özellikler , gerçek üsler için bu tanımlarla doğru kalır. İkinci tanım, doğrudan karmaşık üslere genelleştirildiği için daha yaygın olarak kullanılır .
Öte yandan, negatif bir gerçek sayının gerçek gücünün üstelleştirilmesi, gerçek olmadığı ve birkaç değeri olabileceği için tutarlı bir şekilde tanımlanması çok daha zordur (bkz. § Negatif tabanlı gerçek üsler ). Asal değer adı verilen bu değerlerden biri seçilebilir , ancak kimliğin kendisi için temel değer seçimi yoktur.
doğru; bkz. § Yetkinin başarısızlığı ve logaritma kimlikleri . Bu nedenle, pozitif bir gerçek sayı olmayan bir temele sahip üs alma, genellikle çok değerli bir işlev olarak görülür .
Rasyonel üslerin limitleri
Herhangi bir irrasyonel sayı , bir rasyonel sayılar dizisinin limiti olarak ifade edilebildiğinden, pozitif bir gerçek sayı b'nin keyfi bir gerçek üslü x ile üslenmesi , kuralla süreklilik ile tanımlanabilir.
burada limit sadece r'nin rasyonel değerleri üzerinden alınır . Bu limit her pozitif b ve her gerçek x için mevcuttur .
Örneğin, x = π ise , sonlanmayan ondalık gösterim π = 3.14159... ve rasyonel güçlerin monotonluğu , istenildiği kadar küçük olan ve içermesi gereken rasyonel güçlerle sınırlanmış aralıkları elde etmek için kullanılabilir.
Böylece, aralıkların üst sınırları ve alt sınırları aynı limite sahip iki dizi oluşturur.
Bu, her pozitif b ve gerçek x için b ve x'in sürekli bir fonksiyonu olarak tanımlar . Ayrıca bkz. İyi tanımlanmış ifade .
üstel fonksiyon
Üstel fonksiyon genellikle olarak tanımlanır nerede olduğunu Euler sayısı . Döngüsel akıl yürütmeden kaçınmak için bu tanım burada kullanılamaz. Böylece, yalnızca pozitif tamsayı üsleriyle üstelleştirmeye dayanan , üstel fonksiyonun ve Euler sayısının bir tanımı verilmiştir. Daha sonra, önceki bölümlerde verilen üs tanımı kullanılırsa, birinin
Üstel işlevi tanımlamanın birçok eşdeğer yolu vardır, bunlardan biri
Biri vardır ve üstel özdeşlik de geçerlidir, çünkü
ve ikinci dereceden terim limiti etkilemez, verim .
Euler sayısı olarak tanımlanabilir . Bu, önceki denklemlerinden aşağıdaki olduğu zaman x bir tamsayıdır (üs tekrarlanan-çarpma tanımındaki bu sonuçlar) 'dir. Eğer x reel ise, önceki bölümlerde verilen tanımlardan, x rasyonel ise üstel özdeşlik , aksi halde üstel fonksiyonun sürekliliği kullanılarak elde edilir.
Üstel işlevi tanımlayan sınır , x'in her karmaşık değeri için yakınsar ve bu nedenle tanımını genişletmek için kullanılabilir ve böylece gerçek sayılardan herhangi bir karmaşık argüman z'ye kadar kullanılabilir . Bu genişletilmiş üstel işlev, üstel özdeşliği sağlamaya devam eder ve genellikle karmaşık taban ve üs için üstelleştirmeyi tanımlamak için kullanılır.
Logaritma yoluyla güçler
Nedir? E X üstel fonksiyon olarak tanımlama, b , x , her pozitif gerçek sayılar için b üstel ve açısından, logaritma fonksiyonu. Özellikle, aslında bu doğal logaritması ln ( x ) olan ters üstel fonksiyon arasında e X bir olduğu anlamına gelir
her b > 0 için . Kimliğin korunması için sahip olunması gereken
Böylece, herhangi bir pozitif gerçek b için alternatif bir b x tanımı olarak kullanılabilir . Bu, rasyonel üsler ve süreklilik kullanılarak yukarıda verilen tanımla uyumludur ve herhangi bir karmaşık üsse doğrudan genişleme avantajıyla.
Pozitif reel tabanlı karmaşık üsler
Eğer b pozitif bir reel sayı, taban ile üs olan b ve karmaşık kompleks bağımsız değişken ile, üstel fonksiyon ortalama ile tanımlanır üs (son see § üstel fonksiyon yukarıdaki gibi)
burada belirtmektedir doğal logaritma arasında b .
Bu kimliği tatmin eder
Genel olarak tanımlanmamıştır, çünkü b z gerçek bir sayı değildir. Karmaşık bir sayının üssüne bir anlam verilirse (aşağıdaki § Karmaşık sayıların kuvvetlerine bakın), genel olarak,
z gerçek veya w tam sayı olmadıkça .
ifade sağlar polar formu arasında açısından gerçek ve sanal parça arasında z , yani
burada mutlak değeri bir trigonometrik faktör biridir. Bu şundan kaynaklanır:
Karmaşık sayıların tamsayı olmayan kuvvetleri
Önceki bölümlerde, tamsayı olmayan üslerle üs alma, yalnızca pozitif reel tabanlar için tanımlanmıştır. Diğer bazlar için, zorluklar içinde görünüşte basit vaka ile zaten görünüyor n üstlerin olduğu inci kökleri, nerede n pozitif bir tam sayıdır. Tamsayı olmayan üstellerle üs genel teorisi için geçerli olsa da , n inci kökleri, bu durumda o kullanmaya gerek olmadığından, ilk dikkat edilmesi gereken hak karmaşık logaritma ve bu nedenle anlamak kolaydır.
bir karmaşık sayının n. kökleri
Her sıfır olmayan bir karmaşık sayı z Witten edilebilir polar bir formu olarak
burada bir mutlak değeri ve z ve onun bir argüman . Argüman, 2 π tamsayı katına kadar tanımlanır ; bu, eğer bir karmaşık sayının argümanı ise, o zaman aynı karmaşık sayının bir argümanı olduğu anlamına gelir .
İki karmaşık sayının çarpımının kutupsal biçimi, mutlak değerlerin çarpılması ve bağımsız değişkenlerin eklenmesiyle elde edilir. Bir kutupsal izler , n , bir karmaşık sayının inci kökü alınarak elde edilebilir , n mutlak değerinin inci kökü tarafından, bağımsız değişkeni bölünmesi n :
Eğer eklenir değişmedi karmaşık sayı, ancak bu ekler arasında tartışmaya n kökü inci ve yeni sağlar n inci kökünü. Bu yapılabilir n süreleri ve sağlayan n n karmaşık sayının inci kökleri.
Biri seçilmesi genel bir n n olarak inci kökü anapara kökü . Ortak seçim seçmektir n kendisi için inci kökü yani, n iki pozitif hayali bölümü ile biriyseniz, büyük gerçek parçasına sahiptir ve inci kökü. Bu ana yapar n bir inci kök sürekli fonksiyon negatif gerçek değerler dışında, bütün kompleks düzlemde radicand . Bu fonksiyon her zamanki eşittir n pozitif reel radicands için inci kökü. Negatif reel radicands ve garip üstellerle için başat n inci kökü, gerçek olmasa da her zamanki n inci kökü gerçek. Analitik devam başlıca bu gösterir , n inci kök benzersizdir kompleks türevlenebilir normal uzanan fonksiyon , n pozitif olmayan reel sayılar olmayan kompleks düzlemine inci kökü.
Karmaşık sayı bir artış sonra da argümanı artırarak sıfır etrafında hareket ettirilirse, karmaşık sayı başlangıç konumuna geri gelir, ve n, kökleri inci edilir dairesel sırası değiştirilebilir (bunlar ile çarpılmıştır ). Bir tanımlamak mümkün değildir Bu göstermektedir n bütün kompleks düzlemde sürekli değildir kök fonksiyonu inci.
birliğin kökleri
N, birlik kökleri th n karmaşık sayılar bu şekilde ağırlık , n = 1 , burada n, pozitif bir tamsayıdır. Ayrık Fourier dönüşümü veya cebirsel denklemlerin cebirsel çözümleri ( Lagrange çözücüsü ) gibi matematiğin çeşitli alanlarında ortaya çıkarlar .
N, n- birlik inci köklerdir N ilk güç olduğu, n, bu üretim özelliğine sahip birlik inci kökleri olarak adlandırılır ilkel n birlik inci kökleri ; onlar form var olan k asal ile n . Birliğin benzersiz ilkel karekökü, birliğin ilkel dördüncü kökleridir ve
N, birlik kökleri tüm th eksprese izin n bir karmaşık sayının kökleri inci z olarak N , belirli bir ürün n- inci kökleri z bir ile N birlik inci kökü.
Geometrik olarak, N ile birlik yalan köklerinin inci birim çember içinde , kompleks düzlemin bir köşelerinde düzenli n -gon gerçek sayı 1 bir tepe.
Sayı olarak ilkel n en küçük pozitif birlik inci kök bağımsız değişken , denir ana ilkel n birlik inci kökü , bazen kısaltılmış ana n birlik inci kök bu terminoloji ile karışabilir olmasına rağmen, temel değer arasında hangisi 1.
karmaşık üstel alma
Üs almanın karmaşık tabanlarla tanımlanması, genel olarak için sonsuz sayıda olası değer olması dışında, önceki bölümde açıklananlara benzer zorluklara yol açar . Bu nedenle, ya gerçek ve pozitif olmayan z değerleri için sürekli olmayan bir temel değer tanımlanır ya da çok değerli bir işlev olarak tanımlanır .
Her durumda, karmaşık logaritma , karmaşık üstelleştirmeyi şu şekilde tanımlamak için kullanılır:
kullanılan karmaşık logaritmanın varyantı nerede , yani bir fonksiyon veya çok değerli bir fonksiyon, öyle ki
Her için z kendi içinde tanımının etki .
ana değer
Temel değer arasında karmaşık bir logaritma yaygın olarak belirtilen, tek fonksiyonu , öyle ki, her bir sıfır olmayan bir karmaşık sayı için z ,
ve sanal parça arasında z tatmin
Karmaşık logaritma temel değer için tanımlanmamıştır o süreksiz negatif gerçek değerleri z ve bunun holomorfik başka (karmaşık türevlenebilir olduğunu). Eğer z gerçek ve pozitif, karmaşık logaritma temel değer doğal logaritmasıdır:
Asal değeri , logaritmanın ana değerinin nerede olduğu olarak tanımlanır .
İşlev , z'nin gerçek ve pozitif olmadığı noktaların komşuluğu dışında holomorfiktir .
Eğer z gerçek ve pozitif, başlıca değeri yukarıda tanımlandığı olağan değer eşittir. Eğer burada n, bir tam sayı olduğu, bu asıl değer yukarıda tanımlanan ile aynıdır.
çok değerli fonksiyon
Bazı bağlamlarda, z'nin negatif reel değerlerinde ve asal değerlerinin süreksizliği ile ilgili bir sorun vardır . Bu durumda bu fonksiyonları çok değerli fonksiyonlar olarak değerlendirmekte fayda var .
Çok değerli logaritmanın değerlerinden birini (tipik olarak temel değeri) belirtirse, diğer değerler k'nin herhangi bir tam sayı olduğu yerdedir . Benzer şekilde, üs almanın bir değeri ise, diğer değerler şu şekilde verilir:
burada k herhangi bir tam sayıdır.
Farklı k değerleri, w bir rasyonel sayı olmadıkça farklı değerler verir , yani dw'nin bir tam sayı olduğu bir d tamsayısı vardır. Bu , üstel fonksiyonun periyodikliğinden kaynaklanır, daha spesifik olarak, eğer ve sadece bir tamsayı katıysa
Eğer bir rasyonel sayıdır m ve n aralarında asal ile daha sonra tam olarak sahip n değerleri. Durumda , bu değerler de tarif edilen ile aynıdır § n karmaşık sayının inci kökleri . Eğer W bir tam sayı olduğu, bu kabul eder yalnızca bir değer olduğu § tamsayı üs .
Çok değerli üs alma, grafiğinin , her noktanın komşuluğunda her birini bir holomorfik işlevi tanımlayan birkaç sayfadan oluşması anlamında holomorfiktir. Eğer z , 0 civarında bir daire boyunca sürekli değişiyorsa , bir dönüşten sonra, tabakanın değeri değişmiş demektir.
Hesaplama
Kanonik şekli arasında kanonik şeklinde hesaplanabilir z ve w . Bu, tek bir formülle açıklanabilmesine rağmen, hesaplamayı birkaç adıma bölmek daha açıktır.
-
Polar bir şekilde bir z . Eğer z'nin kanonik formu ise( a ve b gerçek), o zaman kutupsal formunerede ve ( bu işlevin tanımı için atan2'ye bakın ).
- Logaritma arasında z . Temel değer bu logaritma olduğuyerdegösterir doğal logaritma . Logaritmanın diğer değerleri,herhangi bir k tamsayısınıneklenmesiyle elde edilir.
-
Kanonik şekilde If ile c ve d gerçek, değerleri vardırkarşılık gelen ana değer
-
Son sonuç. kimlikleri kullanarak ve biri alırile ana değer için.
Örnekler
-
Kutupsal i olduğu ve değerleri bu şekilde olanBunu takip ediyorYani, tüm değerleri gerçektir, asıl olan
-
Benzer şekilde, -2'nin kutupsal formu So'dur , yukarıda açıklanan yöntem değerleri verir.Bu durumda, tüm değerler aynı argümana ve farklı mutlak değerlere sahiptir.
Her iki örnekte de tüm değerleri aynı argümana sahiptir. Ancak ve ancak Daha genel olarak, bu doğrudur , gerçek kısmı ve w bir tamsayıdır.
Güç ve logaritma kimliklerinin başarısızlığı
Kuvvetler için bazı özdeşlikler ve pozitif gerçek sayılar için logaritmalar, karmaşık kuvvetler ve karmaşık logaritmalar ne kadar tek değerli fonksiyonlar olarak tanımlanırsa tanımlansın, karmaşık sayılar için başarısız olacaktır . Örneğin:
- log( b x ) = x ⋅ log b özdeşliği , b pozitif bir gerçek sayı ve x bir gerçek sayı olduğunda geçerlidir. Ancak karmaşık logaritmanın
ana dalı için
Logaritmanın hangi dalının kullanıldığına bakılmaksızın, benzer bir özdeşlik hatası olacaktır. Söylenebilecek en iyi şey (yalnızca bu sonucu kullanarak) şudur:
Bu kimlik, log'u çok değerli bir fonksiyon olarak değerlendirirken bile geçerli değildir. Olası değerleri log ( w , z ) kişilerce içeren z ⋅ günlük ağırlık bir şekilde uygun bir alt kümesi . log( w ) ve m , n'nin ana değeri için Log( w ) kullanarak herhangi bir tam sayı olarak her iki tarafın olası değerleri şunlardır:
- ( bc ) x = b x c x ve ( b / c ) x = b x / c x özdeşlikleri , b ve c pozitif gerçek sayılar ve x bir gerçek sayı olduğunda geçerlidir. Ancak, temel değerler için, bir
ve
Öte yandan, x bir tamsayı olduğunda, özdeşlikler sıfırdan farklı tüm karmaşık sayılar için geçerlidir.
Üs çok değerli bir fonksiyonu olarak kabul edilirse o zaman muhtemel değerler (-1 ⋅ 1) 1/2 olan {1, -1 }. Özdeşlik geçerlidir, ancak {1} = {(−1 ⋅ −1) 1/2 } demek yanlıştır. - ( e x ) y = e xy özdeşliği x ve y gerçek sayıları için geçerlidir , ancak karmaşık sayılar için doğruluğunu varsaymak, Clausen tarafından 1827'de keşfedilen aşağıdaki paradoksa yol açar : Herhangi bir n tamsayı için , elimizde:
- ( her iki tarafın -th gücünü alarak )
- ( üslü kullanma ve genişletme)
- (kullanarak )
- ( e ile bölerek )
Mantıksızlık ve aşkınlık
Eğer b pozitif gerçek cebirsel sayı ve x , rasyonel sayıdır sonra b x bir cebirsel sayıdır. Bu cebirsel uzantılar teorisinden kaynaklanmaktadır . Bu, b herhangi bir cebirsel sayıysa doğrudur , bu durumda, b x'in tüm değerleri (bir çok değerli fonksiyon olarak ) cebirseldir. Eğer X bir akıl (olduğunu rasyonel değildir ), ve her ikisi de B ve X cebirsel olarak, Gelfond-Schneider teoremi tüm değerleri iddia b x olan aşkın durumlar dışında, (cebirsel değildir) b eşittir 0 veya 1 .
Başka bir deyişle, x irrasyonel ise ve o zaman b , x ve b x'ten en az biri aşkındır.
Cebirde tamsayı kuvvetleri
Tekrarlanan çarpma olarak pozitif tamsayı üsleriyle üs alma tanımı, çarpma olarak belirtilen herhangi bir ilişkilendirme işlemi için geçerli olabilir . tanımı, ayrıca bir çarpımsal kimliğin varlığını gerektirir .
Çarpımsal olarak gösterilen bir ilişkisel işlemle birlikte bir kümeden ve 1 ile gösterilen bir çarpımsal özdeşlikten oluşan bir cebirsel yapı bir monoiddir . Böyle bir monoidde, bir x elemanının üslenmesi endüktif olarak şu şekilde tanımlanır:
- her negatif olmayan tamsayı için n .
Eğer n, negatif bir tam sayı olduğu, sadece tanımlanan X bir sahiptir çarpımsal ters . Bu durumda, x'in tersi gösterilir ve şu şekilde tanımlanır:
Tamsayı üsleriyle üs alma , cebirsel yapıdaki x ve y ile m ve n tamsayıları için aşağıdaki yasalara uyar :
Bu tanımlar matematiğin birçok alanında, özellikle gruplar , halkalar , alanlar , kare matrisler (bir halka oluşturan) için yaygın olarak kullanılmaktadır . Bunlar için de geçerlidir fonksiyonları , bir gelen dizi altında Monoid meydana kendisi için işlev bileşim . Bu, belirli örnekler olarak, herhangi bir matematiksel yapının geometrik dönüşümlerini ve endomorfizmlerini içerir .
Tekrarlanabilecek birkaç işlem olduğunda, tekrarlanan işlemin sembolünü üsten önce üst simgeye yerleştirerek belirtmek yaygındır. Örneğin, f a, gerçek işlevi olan çarpılabilir değerli, çarpımın ilgili üs temsil eder, ve ilgili olan üs ifade edebilir işlev bileşimi . Yani,
ve
Genel olarak, ifade edilir ise belirtilmektedir
Grup içinde
Bir çarpımsal grubu bir şekilde olan dizi birleştirici işlem türünde bir çarpma olarak gösterilmektedir, kimlik elemanının her eleman bir ters sahip olduğu ve bu.
Yani, eğer G bir grupsa, her n tamsayı için tanımlanır .
Bir grubun bir elemanının tüm güçlerinin kümesi bir alt grup oluşturur . Belirli bir elemanı güçlerin oluşan bir grup (ya da alt-grubu) x olduğu siklik grup tarafından üretilen x . Tüm yetkileri ise x farklıdır, grup izomorf için katkı grubun tamsayılar. Aksi takdirde, siklik gruptur sonlu (bu elementlerin sonlu sayıda) ve elemanların kendi sayıdır düzeni bir x . Sırası varsa , x olduğu , n , daha sonra tarafından oluşturulan siklik grup x oluşur , n ilk güçler x (üsten kayıtsız başlangıç 0 ya da 1 ).
Elemanların sırası grup teorisinde temel bir rol oynar . Örneğin, sonlu bir gruptaki bir elemanın mertebesi her zaman grubun eleman sayısının (grubun mertebesi ) bölenidir. Grup elemanlarının olası sıraları, bir grubun yapısının incelenmesinde (bkz. Sylow teoremleri ) ve sonlu basit grupların sınıflandırılmasında önemlidir .
Üst simge gösterimi de kullanılır konjugasyon ; yani, g h = h -1 gh , burada g ve h bir grubun elemanlarıdır. Üst simge bir tamsayı olmadığı için bu gösterim üs ile karıştırılamaz. Bu gösterimin motivasyonu, konjugasyonun bazı üs yasalarına uymasıdır, yani ve
bir halkada
Bir halkada , bazı sıfır olmayan öğelerin bazı n tamsayılarını karşıladığı ortaya çıkabilir . Böyle bir element denir nilpotent . Bir de değişmeli halka , üstel sıfır elemanları oluşturan ideali olarak adlandırılan, nilradical halkasının.
Nilradical şekilde ayarlanır sıfır ideale (eğer olduğunu ima her pozitif tam sayı için n ), değişmeli halka bahsedilen olan düşük . Bir afin cebirsel kümenin koordinat halkası her zaman bir indirgenmiş halka olduğundan, cebirsel geometride indirgenmiş halkalar önemlidir .
Daha genel olarak, bir tanesi belirli bir I değişmeli bir halka içinde , R , bir elemanları seti , R bir güce sahip I ideal olarak adlandırılan bir kökü arasında I . Nilradikal, sıfır idealin radikalidir . Bir radikal İdeal kendi radikal eşittir bir idealdir. Bir k alanı üzerindeki bir polinom halkasında , bir ideal, ancak ve ancak bir afin cebirsel kümede sıfır olan tüm polinomların kümesi ise radikaldir (bu, Hilbert'in Nullstellensatz'ının bir sonucudur ).
Matrisler ve lineer operatörler
Eğer bir daha sonra ürün, bir kare matris, bir A kendisi ile n olarak adlandırılır kez matris gücü . Ayrıca birim matris olarak tanımlanır ve eğer A ters çevrilebilirse, o zaman .
Matris güçleri genellikle ayrık dinamik sistemler bağlamında ortaya çıkar ; burada matris A , bir sistemin x durum vektöründen sistemin bir sonraki Ax durumuna geçişi ifade eder . Bu, örneğin bir Markov zincirinin standart yorumudur . Sonra , iki zaman adımından sonra sistemin durumu ve benzeri: n zaman adımından sonra sistemin durumu . Matris gücü , şimdiki durum ile gelecekteki n adımlık bir zamandaki durum arasındaki geçiş matrisidir . Dolayısıyla matris güçlerini hesaplamak, dinamik sistemin evrimini çözmeye eşdeğerdir. Çoğu durumda, matris güçleri, özdeğerler ve özvektörler kullanılarak amaca uygun bir şekilde hesaplanabilir .
Matrislerin yanı sıra daha genel lineer operatörler de üstelleştirilebilir. Yeni bir fonksiyon vermek için fonksiyonlar üzerinde hareket eden lineer bir operatör olan kalkülüsün türev operatörü buna bir örnektir . N, farklılaşma operatörün inci gücü n türevi inci:
Bu örnekler doğrusal operatörlerin ayrık üsleri içindir, ancak birçok durumda bu operatörlerin güçlerini sürekli üslerle tanımlamak da istenir. Bu, yarıgrupların matematiksel teorisinin başlangıç noktasıdır . Nasıl ayrık üslü hesaplama matris güçleri ayrık dinamik sistemleri çözüyorsa, sürekli üslü hesaplama matris güçleri de sürekli dinamik sistemleri çözer. Örnekler, ısı denklemini , Schrödinger denklemini , dalga denklemini ve bir zaman evrimini içeren diğer kısmi diferansiyel denklemleri çözme yaklaşımlarını içerir . Türev operatörünü tamsayı olmayan bir güce üslendirmenin özel durumuna , kesirli integral ile birlikte kesirli hesabın temel işlemlerinden biri olan kesirli türev denir .
sonlu alanlar
Bir alan çarpma, toplama, çıkarma ve bölme tanımlandığı gibidir ve çarpma olduğu özellikleri tatmin edildiği bir cebirsel yapıdır birleştirici ve her sıfır olmayan türünde bir çarpımsal ters . Bu, 0'ın pozitif olmayan güçleri dışında tamsayı üsleriyle üs almanın iyi tanımlandığı anlamına gelir . Yaygın örnekler, bu makalenin önceki bölümlerinde ele alınan karmaşık sayılar ve bunların alt alanları , rasyonel sayılar ve gerçek sayılardır ve tümü sonsuzdur .
Bir sonlu alan bir olan bir alan olup sonlu sayıda eleman. Bu eleman sayısı ya bir asal sayıdır ya da bir asal kuvvettir ; yani, p'nin bir asal sayı ve k'nin pozitif bir tam sayı olduğu forma sahiptir . Böyle her q için , q elemanlı alanlar vardır . Bulunan alanlar q elemanlarının hepsi izomorfik ile tek bir alan vardır sanki çalışma, genel olarak, izin veren, q , elemanları ifade
Birinde var
her biri için
Bir ilkel eleman olarak bir elementtir Gı gibi set q 1 - ilk güçler g (olduğundan, ) 'in sıfırdan farklı elemanlar kümesini eşittir vardır ilkel elemanlar burada olduğu totient .
In freshman'ın rüyası kimliği
p üssü için doğrudur . As içinde Haritanın izler
olduğu lineer üzerinde ve bir olan tarla otomorfizm denilen Frobemino otomorfizma . Eğer alan vardır k olan otomorfizim, k (altındaki ilk güçler bileşimin arasında) F . Diğer bir deyişle, Galois grubu arasında olan siklik düzenin k Frobemino otomorfizması tarafından oluşturulan.
Diffie-Hellman anahtar değişimi yaygın kullanılan sonlu alanlarda üs bir uygulamadır güvenli iletişim . Üstel almanın hesaplama açısından ucuz olduğu gerçeğini kullanır, oysa ters işlem, ayrık logaritma , hesaplama açısından pahalıdır. Eğer Daha kesin olarak, g olan bir ilkel eleman daha sonra verimli bir şekilde hesaplanabilmektedir karesi alınarak üs herhangi e bile, q almak sağlayan bilinen bir algoritma var ise, büyük, e gelen eğer q, yeterince büyüktür.
kümelerin güçleri
Kartezyen ürün iki set G ve T setidir sipariş çiftlerinin şekildedir ve bu işlem uygun şekilde değil değişmeli veya birleştirici , ancak şu özelliklere sahiptir kadar kanonik izomorfizm Örneğin, belirli izin, ve
Bu belirleme sağlar n inci güç kümesi ait S tüm set olarak n - dizilerini unsurlarının S .
Ne zaman S bazı yapıya sahip olduğunu, o kadar sık olduğunu doğal olarak benzer bir yapıya sahip olduğunu. Bu durumda, genellikle "Kartezyen çarpım" yerine " doğrudan çarpım " terimi kullanılır ve üs alma, ürün yapısını ifade eder. Örneğin (burada gerçek sayıları belirtir), vektör uzayı , topolojik uzaylar , halkalar , vb. gibi doğrudan çarpımlarının yanı sıra n kopyasının Kartezyen çarpımını belirtir .
Üs olarak ayarlar
Bir n- -tuple elemanlarının S bir olarak kabul edilebilir fonksiyonu ile ilgili aşağıdaki gösterim Bu genelleştirmektedir.
İki oluşturduğunun göz önüne alındığında S ve T , tüm fonksiyonların kümesi T için S belirtilir (bkz ilki için bu üstel gösterim aşağıdaki kanonik izomorfizmleri tarafından haklı Currying ):
nerede Kartezyen ürün ve belirtir ayrık birliği .
Kümeler üzerindeki diğer işlemler için, tipik olarak değişmeli grupların , vektör uzaylarının veya modüllerin doğrudan toplamları için kümeler üs olarak kullanılabilir . Doğrudan toplamları doğrudan ürünlerden ayırt etmek için, doğrudan toplamın üssü parantezler arasına yerleştirilir. Örneğin , sonsuz sayıda reel sayı dizilerinin vektör uzayını ve sonlu sayıda sıfır olmayan elemana sahip dizilerin vektör uzayını gösterir. İkinci bir sahiptir temel eşittir tam olarak bir sıfır olmayan bir elemanı ile dizilerinden oluşan 1 ise, Hamel bazlar (orada varlığı içerir, çünkü önceki açık bir şekilde tarif edilemez Zorn'un Lemmasını ).
Bu bağlamda, 2 kutu kümesini temsil eder , Bu yüzden belirtmektedir güç grubu ve S işlevlerin kümesidir, S için hangi grubu ile tespit edilebilir alt kümeleri arasında , S , her bir fonksiyonu eşleyerek ters görüntüsü arasında 1 .
İle bu uyuyor kardinal sayıların üs anlamında, yani | S T | = | S | | T | , nerede | X | X'in kardinalitesidir .
Kategori teorisinde
Gelen setlerinin kategorisinde , morfizma setleri arasında X ve Y den fonksiyonları X için Y . Bu işlevlerin grubu olduğu sonuçlanan X için Y gösterilir da belirtilecektir edilebilir önceki bölümde izomorfizm yeniden olabilir
Bu, " T kuvvetine üs " işlevcisinin, " T ile doğrudan çarpım" işlevine sağ ek olduğu anlamına gelir .
Bu, sonlu doğrudan ürünlerin var olduğu bir kategoride üstelleştirme tanımına genelleşir : böyle bir kategoride, işlev varsa, işleve bir sağ bitişiktir A kategorisi , eğer doğrudan ürünler varsa, Kartezyen kapalı kategori olarak adlandırılır , ve functor'un her T için bir sağ eki vardır .
tekrarlanan üs
Nasıl ki doğal sayıların üsleri tekrarlı çarpma ile motive ediliyorsa, tekrarlı üslere dayalı bir işlem tanımlamak da mümkündür; bu işleme bazen hyper-4 veya tetration denir . Tetrasyonun yinelenmesi başka bir işleme yol açar ve bu şekilde hiperişlem adında bir kavram . Bu işlem dizisi, Ackermann işlevi ve Knuth'un yukarı ok gösterimi ile ifade edilir . Tıpkı üs almanın toplamadan daha hızlı büyüyen çarpmadan daha hızlı büyümesi gibi, tetraasyon da üs almadan daha hızlı büyüyor. (3, 3) 'de değerlendirilir, toplama, çarpma, üs alma ve tetratasyon fonksiyonları 6, 9, 27 veSırasıyla 7 625 597 484 987 ( = 3 27 = 3 3 3 = 3 3 ).
yetki sınırları
Sıfırın sıfırın kuvvetine göre, 0 0 belirsiz biçiminde olan bir dizi limit örneği verir . Bu örneklerdeki limitler mevcuttur, ancak iki değişkenli x y fonksiyonunun (0, 0) noktasında limiti olmadığını gösteren farklı değerlere sahiptir . Bu fonksiyonun hangi noktalarda limiti olduğu düşünülebilir.
Daha doğrusu, D = {( x , y ) ∈ R 2 : x > 0} üzerinde tanımlanan f ( x , y ) = x y fonksiyonunu düşünün . Daha sonra D bir alt kümesi olarak düşünülebilir R 2 olduğu (burada, bütün çiftlerin grubu ( x , y ) ile x , y ait genişletilmiş reel sayı çizgisi R = [-∞ + ∞] , sahip ürün f fonksiyonunun bir limite sahip olduğu noktaları içerecek olan topology ) .
Aslında, ön hiç bir sınır vardır yığılma noktaları arasında D haricinde (0, 0) , (+ ∞, 0) , (1 + ∞) ve (1, -∞) . Bu duruma göre, bu güçler tanımlamak için bir olanak sağlar x y süreklilik zaman 0 ≤ x ≤ + ∞ , -∞ ≤ y ≤ + ∞ , 0 hariç 0 , (+ ∞) 0 , 1 + ∞ ve 1 -∞ kalır, belirsiz formlar
Bu süreklilik tanımına göre şunları elde ederiz:
- x +∞ = +∞ ve x −∞ = 0 , 1 < x ≤ +∞ olduğunda .
- x +∞ = 0 ve x −∞ = +∞ , 0 ≤ x < 1 olduğunda .
- 0 y = 0 ve (+∞) y = +∞ , 0 < y ≤ +∞ olduğunda .
- 0 y = +∞ ve (+∞) y = 0 , −∞ ≤ y < 0 olduğunda .
Bu güçler sınırlarını alarak elde edilir x , y için pozitif değerler x . Bu yöntem, x < 0 olduğunda bir x y tanımına izin vermez , çünkü ( x , y ) x < 0 ile çiftler D'nin birikim noktaları değildir .
Öte yandan, n bir tamsayı olduğunda, x n kuvveti , negatif olanlar da dahil olmak üzere , x'in tüm değerleri için zaten anlamlıdır . Bu, n tek olduğunda , negatif n için yukarıda elde edilen 0 n = +∞ tanımını sorunlu hale getirebilir , çünkü bu durumda x n → +∞ , x pozitif değerler yoluyla 0'a eğilim gösterir , ancak negatif değerler değildir.
Tamsayı üsleri ile verimli hesaplama
Bilgisayar b N tekrarlanan çarpma kullanarak gerektirir , n 1 - çarpma işlemleri, ancak aşağıdaki örnek ile gösterildiği gibi, daha etkin bir şekilde daha hesaplanabilir. 2 100 değerini hesaplamak için, ikili olarak yazılmış 100 üssüne Horner kuralını uygulayın :
- .
Daha sonra Horner kuralını sağdan sola okuyarak aşağıdaki terimleri sırayla hesaplayın.
| 2 2 = 4 |
| 2 (2 2 ) = 2 3 = 8 |
| (2 3 ) 2 = 2 6 = 64 |
| (2 6 ) 2 = 2 12 =4096 |
| (2 12 ) 2 = 2 24 =16 777 216 |
| 2 (2 24 ) = 2 25 =33 554 432 |
| (2 25 ) 2 = 2 50 =1 125 899 906 842 624 |
| (2 50 ) 2 = 2 100 =1 267 650 600 228 229 401 496 703 205 376 |
Bu adım dizisi, 99 yerine yalnızca 8 çarpma gerektirir.
Genel olarak, çarpma işlemlerinin sayısının hesaplanması için gereken b , n indirgenebilir kullanılarak karesi alınarak üs burada, sayısını belirtmektedir 1 içinde ikili gösterimine ait n . Bazı üsler için (100 bunların arasında değildir), çarpma sayısı, minimum toplama zinciri üstelleştirmesi hesaplanarak ve kullanılarak daha da azaltılabilir . Bulma az için çarpımların dizisini (üs için en az uzunlukta katılma zincir) b n bir verimli algoritmalar anda bilindiği zor bir problem, (bakınız, alt küme toplamı sorunu ), ancak birçok oldukça verimli algoritmalar mevcuttur. Bununla birlikte, pratik hesaplamalarda, kare alarak üstel alma yeterince verimlidir ve uygulanması çok daha kolaydır.
Yinelenen işlevler
Fonksiyon kompozisyon bir olan ikili işlem tanımlanır fonksiyonları öyle ki değer kümesi sağda yazılı fonksiyon dahildir etki solda yazılı işlevin. olarak gösterilir ve tanımlanır
f'nin etki alanındaki her x için .
Bir fonksiyonu alanı ise f onun değer kümesi eşit bir kendisi ile bir zaman rasgele sayıda fonksiyonu oluşturmak olabilir ve bu tanımlar , n bileşimin altında fonksiyon inci gücü, yaygın olarak adlandırılan N yineleme inci fonksiyon. Bu nedenle , genel olarak gösterir n yineleme th f ; örneğin, şu anlama gelir
Fonksiyonun kod alanında bir çarpma tanımlandığında, bu, fonksiyonlar üzerinde bir çarpma tanımlar, noktasal çarpma , başka bir üs almaya neden olur. Kullanıldığında , fonksiyonel gösterimi , üs iki çeşit genellikle pek fonksiyonel iterasyon üs yerleştirilmesi ile ayırt edilir önce parantez fonksiyon bağımsız değişkenler sarılması, ve noktasal çarpma üs yerleştirilmesi sonra parantez. Bu nedenle ve İşlevsel gösterim kullanılmadığında, anlam ayrımı genellikle bileşim sembolü üssün önüne yerleştirerek yapılır; örneğin ve Tarihsel nedenlerden dolayı, tekrarlanan bir çarpmanın üssü, tipik olarak trigonometrik fonksiyonlar olmak üzere bazı özel fonksiyonlar için argümanın önüne yerleştirilir . Yani ve her durumda, nadiren düşünülen her ikisi de demek değildir . Tarihsel olarak, bu gösterimlerin çeşitli varyantları farklı yazarlar tarafından kullanılmıştır.
Bu bağlamda , eğer varsa , üs daima ters fonksiyonu ifade eder . Yani için çarpımsal ters kesirler genellikle olduğu gibi kullanılır
programlama dillerinde
Programlama dilleri , üst simgeleri desteklemeyen doğrusal gösterimler olduklarından, genellikle üstelleştirmeyi bir infix operatörü veya bir (önek) işlevi olarak ifade eder:
-
x ↑ y: Algol , Commodore BASIC , TRS-80 Level II/III TEMEL . -
x ^ y: AWK , BASIC , J , MATLAB , Wolfram Language ( Mathematica ), R , Microsoft Excel , Analytica , TeX (ve türevleri), TI-BASIC , bc (tamsayı üsleri için), Haskell (negatif olmayan tamsayı üsleri için), Lua ve çoğu bilgisayar cebir sistemi . Sembolün çelişkili kullanımları^şunları içerir: XOR (POSIX Shell aritmetik genişletmesinde, AWK, C, C++, C#, D, Go, Java, JavaScript, Perl, PHP, Python, Ruby ve Tcl), dolaylı (Pascal) ve dize bitiştirme (OCaml ve Standart ML). -
x ^^ y: Haskell (kesirli taban, tamsayı üsleri için), D . -
x ** y: Ada , Z kabuğu , KornShell , Bash , COBOL , CoffeeScript , Fortran , FoxPro , Gnuplot , Groovy , JavaScript , OCaml , F # , Perl , PHP , PL / I , Python , Rexx , Yakut , SAS , seed7 , Tcl , ABAP , Mercury , Haskell (kayan noktalı üsler için), Turing , VHDL . -
pown x y: F# (tamsayı tabanı, tamsayı üs için). -
x⋆y: APL .
Diğer birçok programlama dili, üs alma için sözdizimsel destekten yoksundur, ancak kitaplık işlevleri sağlar:
-
pow(x, y): C , C++ . -
Math.Pow(x, y): C# . -
math:pow(X, Y): Erlang . -
Math.pow(x, y): Java . -
[Math]::Pow(x, y): PowerShell . -
(expt x y): Ortak Lisp .
Bazı üstler için hesaplama için özel metodlar var x , y çok daha hızlı jenerik üs aracılığıyla daha. Bu olgular, küçük pozitif bir tamsayı içerir (tercihen X · x üzerinde x 2 ; tercih 1 / X üzerinde X -1 ) ve kökler (tercih SQRT ( X ) boyunca x 0.5 , tercih Bankası ( x ) boyunca x 1/3 ).
Tüm programlama dilleri üs için aynı dernek kuralına uymak: iken Wolfram dil , Google Arama ve diğerleri (yani sağ dernek kullanmak a^b^colarak değerlendirilir a^(b^c)), gibi birçok bilgisayar programları , Microsoft Office Excel ve Matlab sola ilişkilendirmek (yani a^b^colduğu olarak değerlendirilir (a^b)^c).












![{\displaystyle \scriptstyle {\sqrt[{\text{derece}}]{\scriptstyle {\text{radicand}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)
























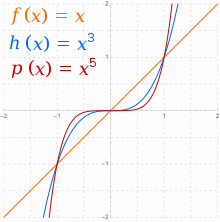


















![{\displaystyle {\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ba2638d05cd9ed8dafae7e34986399e48ea99)















![{\displaystyle \sol[b^{3},b^{4}\sağ],\sol[b^{3.1},b^{3.2}\sağ],\sol[b^{3.14},b^ {3.15}\sağ],\sol[b^{3.141},b^{3.142}\sağ],\sol[b^{3.1415},b^{3.1416}\sağ],\sol[b^{3.14159 },b^{3.14160}\sağ],\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09aec126692a109ddd2b003c78002512678e923)


































![{\displaystyle \left(\rho e^{i\theta }\sağ)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc4ae73419a2cabb0133293dc1bfa19d743b1d9)











































































































![{\displaystyle k[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37c2b680cd4b215ac5c3c548a0e596d534526cab)



































































