Ters hiperbolik fonksiyonlar - Inverse hyperbolic functions

In matematik , ters hiperbolik fonksiyonlar olan ters fonksiyonlar arasında hiperbolik fonksiyonlar .

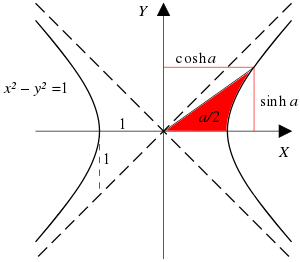
Bir hiperbolik fonksiyonun belirli bir değeri için, karşılık gelen ters hiperbolik fonksiyon, karşılık gelen hiperbolik açıyı sağlar . Hiperbolik açısının büyüklüğü eşit alana karşılık gelen hiperbolik sektör hiperbol xy = 1 ya da karşılık gelen sektörün iki alan birimi hiperbol x ² - y ² = 1 , bir tam olarak dairesel açılı iki katıdır alan dairesel sektörün bir birim çember . Bazı yazarlar , hiperbolik açıları gerçekleştirmek için ters hiperbolik fonksiyonlara " alan fonksiyonları " adını vermişlerdir .

Hiperbolik geometride açıların ve uzaklıkların hesaplanmasında hiperbolik fonksiyonlar ortaya çıkar . Aynı zamanda, bir çok doğrusal Çözeltilerin meydana diferansiyel denklemler (örneğin, bir tanımlayıcı denklem olarak katener ) kübik denklem ve Laplace denklemi olarak kartezyen koordinatları . Laplace denklemleri , elektromanyetik teori , ısı transferi , akışkanlar dinamiği ve özel görelilik dahil olmak üzere fiziğin birçok alanında önemlidir .

gösterim

En yaygın kısaltmalar, ISO 80000-2 standardı tarafından belirtilenlerdir . Bunlar; ar- gelen hiperbolik fonksiyonu (örneğin, arsinh, arcosh) kısaltması eklenmiştir.

Bununla birlikte, ark- ve ardından karşılık gelen hiperbolik fonksiyon (örneğin, arcsinh, arccosh), ters trigonometrik fonksiyonlar için terminolojiye benzer şekilde yaygın olarak görülür . Öneki yana bu misnomers olan ark kısaltmasıdır arcus önek ise, ar açılımı alan ; hiperbolik fonksiyonlar doğrudan yaylarla ilgili değildir.

Diğer yazarlar notasyonu kullanmayı tercih arg SİNH, argcosh, argtanh ve benzeri, önek nerede arg Latince kısaltmasıdır Argumentum . Bilgisayar biliminde bu genellikle asinh olarak kısaltılır .

sinh ⁻¹ ( x ) , cosh ⁻¹ ( x ) vb . gösterimi de kullanılır, bununla birlikte, bir stenografi yerine bir güç olarak üst simge −1'in yanlış yorumlanmasından kaçınmak gerekir. ters fonksiyon (örneğin, cosh ⁻¹ ( x ) ve cosh( x ) ⁻¹ ).

Logaritma açısından tanımlar

Yana hiperbolik fonksiyonlar olan rasyonel fonksiyonlar arasında E ^x pay ve payda en ikide derece olan, açısından çözülebilir bu fonksiyonlar e ^X , kullanılarak kuadratik formül ; daha sonra doğal logaritmayı alarak ters hiperbolik fonksiyonlar için aşağıdaki ifadeleri verir.

İçin karmaşık argümanlar, ters hiperbolik fonksiyonlar, karekök ve logaritma olan çoklu değerli fonksiyonlar ve bir sonraki alt bölümlerin denklikleri çok değerli fonksiyonların eşitlikler olarak görülebilir.

Tüm ters hiperbolik fonksiyonlar için (ters hiperbolik kotanjant ve ters hiperbolik kosekant hariç), gerçek fonksiyonun etki alanı bağlıdır .

Ters hiperbolik sinüs

Ters hiperbolik sinüs (aka alan hiperbolik sinüs) (Latince: Alan sinüs hiperbolikusu ):

${\displaystyle \operatöradı {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\sağ)}$

Etki alanı tüm gerçek çizgidir .

Ters hiperbolik kosinüs

Ters hiperbolik kosinüs (diğer adıyla alan hiperbolik kosinüs ) (Latince: Area cosinus hyperbolicus ):

${\displaystyle \operatöradı {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\sağ)}$

Etki alanı [1, +∞ ) kapalı aralığıdır .

Ters hiperbolik tanjant

Ters hiperbolik tanjant (diğer adıyla hiperbolik tanjant ) (Latince: Area tangens hyperbolicus ):

${\displaystyle \operatöradı {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\sağ)}$

Etki alanı açık aralıktır (-1, 1) .

Ters hiperbolik kotanjant

Ters hiperbolik kotanjant (aka, alan hiperbolik kotanjant ) (Latince: Area cotangens hyperbolicus ):

${\displaystyle \operatöradı {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\sağ)}$

Tanım alanı (−∞, −1) ve (1, +∞) açık aralıklarının birleşimidir .

Ters hiperbolik sekant

Ters hiperbolik sekant (aka, alan hiperbolik sekant ) (Latince: Area secans hyperbolicus ):

${\displaystyle \operatöradı {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right )=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\sağ)}$

Etki alanı yarı açık aralıktır (0, 1] .

Ters hiperbolik kosekant

Ters hiperbolik kosekant (aka, alan hiperbolik kosekant ) (Latince: Area cosecans hyperbolicus ):

${\displaystyle \operatöradı {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right )}$

Etki alanı, 0'ın kaldırıldığı gerçek satırdır.

Toplama formülleri

${\displaystyle \operatöradı {arsinh} u\pm \operatöradı {arsinh} v=\operatöradı {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u) ^{2}}}\sağ)}$

${\displaystyle \operatöradı {arcosh} u\pm \operatöradı {arcosh} v=\operatöradı {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1) )}}\sağ)}$

${\displaystyle \operatöradı {artanh} u\pm \operatöradı {artanh} v=\operatöradı {artanh} \left({\frac {u\pm v}{1\pm uv}}\sağ)}$

${\displaystyle \operatöradı {arcoth} u\pm \operatöradı {arcoth} v=\operatöradı {arcoth} \left({\frac {1\pm uv}{u\pm v}}\sağ)}$

${\displaystyle {\begin{aligned}\operatöradı {arsinh} u+\operatöradı {arcosh} v&=\operatöradı {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}) -1)}}\right)\\&=\operatöradı {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\ sağ)\end{hizalanmış}}}$

diğer kimlikler

${\displaystyle {\begin{aligned}2\operatöradı {arcosh} x&=\operatöradı {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatöradı {arcosh} x&=\operatöradı {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatöradı {arsinh} x&=\ operatöradı {arcosh} (2x^{2}+1)&\quad {\hbox{ for }}x\geq 0\\4\operatöradı {arsinh} x&=\operatöradı {arcosh} (8x^{4}+8x ^{2}+1)&\quad {\hbox{ for }}x\geq 0\end{hizalı}}}$

${\displaystyle \ln(x)=\operatöradı {arcosh} \left({\frac {x^{2}+1}{2x}}\sağ)=\operatöradı {arsinh} \left({\frac {x) ^{2}-1}{2x}}\sağ)=\operatöradı {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\sağ)}$

Hiperbolik ve ters hiperbolik fonksiyonların bileşimi

${\displaystyle {\begin{hizalanmış}&\sinh(\operatöradı {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{for}}\quad |x|>1 \\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x< 1\\&\cosh(\operatöradı {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatöradı {artanh} x)={\frac {1}{\ sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{ \sqrt {1+x^{2}}}}\\&\tanh(\operatöradı {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad { \text{for}}\quad |x|>1\end{hizalı}}}$

Ters hiperbolik ve trigonometrik fonksiyonların bileşimi

${\displaystyle \operatöradı {arsinh} \left(\tan \alpha \right)=\operatöradı {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha) }{\cos \alpha }}\sağ)=\pm \operatöradı {arcosh} \left({\frac {1}{\cos \alpha }}\sağ)}$

${\displaystyle \ln \left(\left|\tan \alpha \right|\right)=-\operatöradı {artanh} \left(\cos 2\alpha \right)}$

Dönüşümler

${\displaystyle \ln x=\operatöradı {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\sağ)=\operatöradı {arsinh} \left({ \frac {x^{2}-1}{2x}}\sağ)=\pm \operatöradı {arcosh} \left({\frac {x^{2}+1}{2x}}\sağ)}$

${\displaystyle \operatöradı {artanh} x=\operatöradı {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\sağ)=\pm \operatöradı {arcosh} \ sol({\frac {1}{\sqrt {1-x^{2}}}}\sağ)}$

${\displaystyle \operatöradı {arsinh} x=\operatöradı {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\sağ)=\pm \operatöradı {arcosh} \ sol({\sqrt {1+x^{2}}}\sağ)}$

${\displaystyle \operatöradı {arcosh} x=\sol|\operatöradı {arsinh} \left({\sqrt {x^{2}-1}}\sağ)\sağ|=\sol|\operatöradı {artanh} \ sol({\frac {\sqrt {x^{2}-1}}{x}}\sağ)\sağ|}$

türevler

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatöradı {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{ \text{ tümü için gerçek }}x\\{\frac {d}{dx}}\operatöradı {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}} ,{\text{ tümü için gerçek }}x>1\\{\frac {d}{dx}}\operatöradı {artanh} x&{}={\frac {1}{1-x^{2}}} ,{\text{ tümü gerçek }}|x|<1\\{\frac {d}{dx}}\operatöradı {arcoth} x&{}={\frac {1}{1-x^{2} }},{\text{ tüm gerçekler için }}|x|>1\\{\frac {d}{dx}}\operatöradı {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ tümü gerçek }}x\in (0,1)\\{\frac {d}{dx}}\operatöradı {arcsch} x&{} için ={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ tüm gerçek }}x{\text{ için, }}0\\\ hariç bitiş{hizalı}}}$

Örnek bir farklılaşma için: θ = arsinh x olsun , yani (burada sinh ² θ = (sinh θ ) ² ):

${\displaystyle {\frac {d\,\operatöradı {arsinh} x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1+\sinh ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.}$

Seri genişletmeler

Yukarıdaki işlevler için genişletme serileri elde edilebilir:

${\displaystyle {\begin{aligned}\operatöradı {arsinh} x&=x-\left({\frac {1}{2}}\sağ){\frac {x^{3}}{3}}+\ sol({\frac {1\cdot 3}{2\cdot 4}}\sağ){\frac {x^{5}}{5}}-\sol({\frac {1\cdot 3\cdot 5 }{2\cdot 4\cdot 6}}\sağ){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\ sol({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\sağ){\frac {x^{2n+1}} {2n+1}},\qquad \left|x\right|<1\end{hizalı}}}$

${\displaystyle {\begin{aligned}\operatöradı {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\sağ){\frac {x^{-2 }}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\sağ){\frac {x^{-4}}{4}}+\left({\ frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\sağ){\frac {x^{-6}}{6}}+\cdots \sağ)\\&=\ln (2x)-\sum _{n=1}^{\infty }\sol({\frac {(2n)!}{2^{2n}(n!)^{2}}}\sağ){\ frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{hizalı}}}$

${\displaystyle {\begin{hizalanmış}\operatöradı {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}, \qquad \left|x\right|<1\end{hizalı}}}$

${\displaystyle {\begin{hizalanmış}\operatöradı {arcsch} x=\operatöradı {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{ 2}}\sağ){\frac {x^{-3}}{3}}+\sol({\frac {1\cdot 3}{2\cdot 4}}\sağ){\frac {x^ {-5}}{5}}-\sol({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\sağ){\frac {x^{-7}}{ 7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n} (n!)^{2}}}\sağ){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{hizalı }}}$

${\displaystyle {\begin{aligned}\operatöradı {arsech} x=\operatöradı {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\ sol({\frac {1}{2}}\sağ){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\ sağ){\frac {x^{4}}{4}}+\sol({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\sağ){\frac {x ^{6}}{6}}+\cdots \sağ)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\ frac {(2n)!}{2^{2n}(n!)^{2}}}\sağ){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\ bitiş{hizalı}}}$

${\displaystyle {\begin{hizalanmış}\operatöradı {arcoth} x=\operatöradı {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3} }{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n= 0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{hizalı}}}$

arsinh x için asimptotik açılım şu şekilde verilir:

${\displaystyle \operatöradı {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\sağ)^{n-1}{\ frac {\sol({2n-1}\sağ)!!}{2n\sol({2n}\sağ)!!}}}{\frac {1}{x^{2n}}}}$

Karmaşık düzlemde temel değerler

Olarak karmaşık fonksiyonlarda , ters hiperbolik fonksiyonlar olan fonksiyonlar birden çok değerli olan analitik noktaları sonlu sayıda hariç. Böyle bir işlev için, tanımlamak için ortak olan temel değer bir etki üzerinde birden çok işlevi belirli bir dal ile çakışmaktadır, aşağıdakilerden oluşan bir tek değerli analitik fonksiyonudur, kompleks düzlemin içinde sonlu sayıda yay (genellikle yarı çizgiler veya çizgi parçaları ) kaldırılmıştır. Bu yaylara dal kesimleri denir . Dalın belirlenmesi, yani her noktada çok değerli fonksiyonun hangi değerinin dikkate alınacağının tanımlanması için, genel olarak belirli bir noktada tanımlanır ve analitik süreklilik yoluyla ana değerin tanım alanında her yerde değer çıkarılır . Mümkün olduğunda, analitik devamlılığa atıfta bulunmadan ana değeri doğrudan tanımlamak daha iyidir.

Örneğin, karekök için asıl değer, pozitif reel kısmı olan karekök olarak tanımlanır . Bu, değişkenlerin pozitif olmayan gerçek değerleri (iki karekökün sıfır gerçek kısmına sahip olduğu) dışında her yerde tanımlanan tek değerli bir analitik işlevi tanımlar. Karekök fonksiyonunun bu temel değeri aşağıda belirtilmiştir. Benzer şekilde, aşağıda gösterilen logaritmanın temel değeri , sanal kısmın en küçük mutlak değere sahip olduğu değer olarak tanımlanır . Logaritmanın iki farklı değerinin minimuma ulaştığı değişkenin pozitif olmayan gerçek değerleri dışında her yerde tanımlanır. ${\displaystyle {\sqrt {x}}}$${\displaystyle \operatöradı {Günlük} }$

Tüm ters hiperbolik fonksiyonlar için temel değer, karekök ve logaritma fonksiyonunun temel değerleri cinsinden tanımlanabilir. Bununla birlikte, bazı durumlarda, logaritma cinsinden Tanımların formülleri , çok küçük ve bir durumda bağlantılı olmayan bir tanım alanı verdiği için doğru bir temel değer vermez .

Ters hiperbolik sinüsün temel değeri

Ters hiperbolik sinüsün temel değeri şu şekilde verilir:

${\displaystyle \operatöradı {arsinh} z=\operatöradı {Günlük} (z+{\sqrt {z^{2}+1}}\,)\,.}$

Karekök argümanı pozitif olmayan bir gerçek sayıdır, ancak ve ancak z sanal eksenin [ i , + i ∞) ve (− i ∞, - i ] aralıklarından birine aitse . logaritma gerçektir, o zaman pozitiftir.Böylece bu formül dal kesimleri [ i , + i ∞) ve (− i ∞, - i ] ile arsinh için bir temel değer tanımlar . Dal kesimlerinin birbirine bağlanması gerektiğinden bu optimaldir. tekil noktalar i ve - i sonsuza.

Ters hiperbolik kosinüsün temel değeri

§ Ters hiperbolik kosinüs'te verilen ters hiperbolik kosinüs formülü uygun değildir, çünkü logaritmanın ve karekökün temel değerlerine benzer şekilde, arkosh'un temel değeri hayali z için tanımlanmaz . Bu nedenle karekök çarpanlara ayrılmalıdır,

${\displaystyle \operatöradı {arcosh} z=\operatöradı {Günlük} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.}$

Karelerinin ana değerleri, her ikisi de tanımlandığı durumlar dışında z gerçek aralığına ait (-∞, 1] . Logaritmanın argümanı, o zaman gerçek ise z gerçek ve aynı işarete sahiptir. Bu nedenle, yukarıdaki formüle gerçek aralığın (−∞, 1] dışında bir asal arkosh değeri tanımlar , bu nedenle benzersiz dal kesimidir .

Ters hiperbolik tanjant ve kotanjantın temel değerleri

§ Tanımlar bölümünde logaritma cinsinden verilen formüller ,

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right) )\\\operatöradı {arcoth} z&={\frac {1}{2}}\operatöradı {Günlük} \left({\frac {z+1}{z-1}}\sağ)\end{hizalı} }}$

ters hiperbolik tanjant ve kotanjantın temel değerlerinin tanımı için. Bu formüllerde, logaritmanın argümanı ancak ve ancak z gerçekse gerçektir. Artanh için, bu argüman gerçek (−∞, 0] aralığındadır , eğer z , (−∞, −1] veya [1, ∞)'ye aitse.arcoth için, logaritmanın argümanı (−∞ ) içindedir. , 0] , ancak ve ancak z gerçek aralığa [-1, 1] aitse .

Bu nedenle, bu formüller, dal kesimlerinin ters hiperbolik tanjant için (−∞, -1] ve [1, ∞) ve ters hiperbolik kotanjant için [-1, 1] olduğu uygun temel değerleri tanımlar .

Dal kesimlerinin yakınında daha iyi bir sayısal değerlendirme göz önüne alındığında, bazı yazarlar, ikincisi z = 0'da çıkarılabilir bir tekillik sunsa da , temel değerlerin aşağıdaki tanımlarını kullanır . İki tanımları gerçek değerleri için farklılık ile . Ait olanlar gerçek değerler için farklı olan . ${\ Displaystyle \ operatör adı {artanh} }$${\görüntüleme stili z}$${\displaystyle z>1}$${\ Displaystyle \ operatör adı {arcoth} }$${\görüntüleme stili z}$${\displaystyle z\in [0,1)}$

${\displaystyle {\begin{hizalanmış}\operatöradı {artanh} z&={\tfrac {1}{2}}\operatöradı {Günlük} \left({1+z}\sağ)-{\tfrac {1}{ 2}}\operatöradı {Günlük} \left({1-z}\sağ)\\\operatöradı {arcoth} z&={\tfrac {1}{2}}\operatöradı {Günlük} \left({1+{ \frac {1}{z}}}\sağ)-{\tfrac {1}{2}}\operatöradı {Günlük} \left({1-{\frac {1}{z}}}\sağ)\ bitiş{hizalı}}}$

Ters hiperbolik kosekantın temel değeri

Ters hiperbolik kosekant için temel değer şu şekilde tanımlanır:

${\displaystyle \operatöradı {arcsch} z=\operatöradı {Günlük} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1} }\,\sağ)}$.

Logaritma ve karekökün argümanları pozitif olmayan gerçek sayılar olmadığında tanımlanır. Böylece karekökün asıl değeri , hayali çizginin [− i , i ] aralığının dışında tanımlanır . Logaritmanın argümanı gerçekse, z sıfırdan farklı bir gerçek sayıdır ve bu, logaritmanın argümanının pozitif olduğu anlamına gelir.

Böylece, asal değer, hayali doğrunun [− i , i ] aralığından oluşan dal kesimi dışında yukarıdaki formülle tanımlanır .

İçin z = 0 , dal kesme dahil olan tek nokta vardır.

Ters hiperbolik sekantın temel değeri

Burada, ters hiperbolik kosinüs durumunda olduğu gibi, karekökü çarpanlarına ayırmamız gerekir. Bu ana değeri verir

${\displaystyle \operatöradı {arsech} z=\operatöradı {Günlük} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z}}+1}}\,{ \sqrt {{\frac {1}{z}}-1}}\sağ).}$

Bir kare kökünün bağımsız değişken, gerçek ise, o zaman Z , gerçek olduğunu ve karelerinin her iki ana değerleri durumlar dışında, tarif edildiği izler z gerçek ve aralıkların birine ait 0], (-∞ ve , [1 +∞) . Logaritmanın argümanı gerçek ve negatif ise, o zaman z de gerçek ve negatiftir. Arsech'in temel değerinin, iki dal kesimi dışında , gerçek aralıklar (−∞, 0] ve [1, +∞) dışında yukarıdaki formülle iyi tanımlandığı sonucu çıkar .

İçin z = 0 , şube kesimler birinde yer alan bir tek nokta vardır.

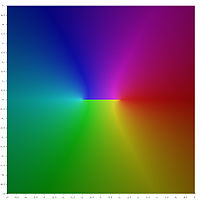
Grafik gösterimi

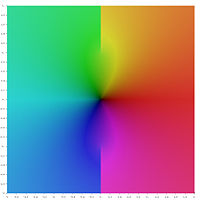
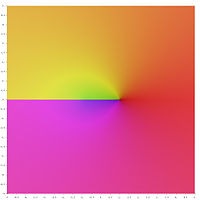
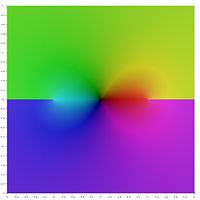
Ters hiperbolik fonksiyonların temel değerlerinin aşağıdaki grafik gösteriminde dal kesimleri rengin süreksizlikleri olarak görünür. Tüm dal kesimlerinin süreksizlikler olarak görünmesi, bu temel değerlerin daha büyük alanlar üzerinde tanımlanan analitik fonksiyonlara genişletilemeyeceğini gösterir. Başka bir deyişle, yukarıda tanımlanan dal kesimleri minimumdur.

Ayrıca bakınız

• karmaşık logaritma
• Hiperbolik sekant dağılımı
• ISO 80000-2
• Ters hiperbolik fonksiyonların integrallerinin listesi

Referanslar

bibliyografya

• Herbert Busemann ve Paul J. Kelly (1953) Projektif Geometri ve Projektif Metrikler , sayfa 207, Academic Press .

Dış bağlantılar

• "Ters hiperbolik fonksiyonlar" , Matematik Ansiklopedisi , EMS Press , 2001 [1994]