cebirsel geometri - Algebraic geometry

Bu Togliatti yüzeyi , beşinci dereceden bir cebirsel yüzeydir . Resmi gerçek bir bölümünü temsil lokusu .

Cebirsel geometri , klasik olarak çok değişkenli polinomların sıfırlarını inceleyen bir matematik dalıdır . Modern cebirsel geometri, bu sıfır kümeleriyle ilgili geometrik problemleri çözmek için esas olarak değişmeli cebirden gelen soyut cebirsel tekniklerin kullanımına dayanmaktadır .

Cebirsel geometri çalışmanın temel nesnelerdir cebirsel çeşitleri geometrik tezahürleri, çözeltiler arasında polinom denklem sistemlerinin . Cebirsel çeşitlerinin en çok çalışılan edilmekte olan sınıflarının örnekleri: düzlem cebirsel eğriler arasında, çizgiler , daireler , parabolas , elips , hiperbollerinin , kübik eğrileri gibi eliptik eğri ve bu gibi quartic eğrileri lemniskatlar ve Cassini oval . Koordinatları belirli bir polinom denklemini sağlıyorsa, düzlemin bir noktası cebirsel bir eğriye aittir . Temel sorular, tekil noktalar , büküm noktaları ve sonsuzluktaki noktalar gibi özel ilgi noktalarının incelenmesini içerir . Daha ileri düzey sorular , eğrinin topolojisini ve farklı denklemler tarafından verilen eğriler arasındaki ilişkileri içerir.

Cebirsel geometri, modern matematikte merkezi bir yere sahiptir ve karmaşık analiz , topoloji ve sayı teorisi gibi çeşitli alanlarla çok sayıda kavramsal bağlantıya sahiptir . Başlangıçta birkaç değişkenli polinom denklem sistemleri üzerine bir çalışma olan cebirsel geometri konusu, denklem çözmenin bittiği yerde başlar ve bir denklem sisteminin çözümlerinin toplamının içsel özelliklerini anlamak, bir denklem bulmaktan daha önemli hale gelir. özel çözüm; bu, hem kavramsal hem de teknik olarak tüm matematiğin en derin alanlarından bazılarına götürür.

20. yüzyılda cebirsel geometri birkaç alt alana ayrıldı.

Cebirsel geometrinin ana akımı, cebirsel çeşitlerin karmaşık noktalarının incelenmesine ve daha genel olarak cebirsel olarak kapalı bir alanda koordinatları olan noktalara ayrılmıştır .
Gerçek cebirsel geometri , cebirsel bir çeşitliliğin gerçek noktalarının incelenmesidir.
Diofant geometrisi ve daha genel olarak, aritmetik geometri koordinatlarına sahip bir cebirsel çeşitli noktalarına çalışmadır alanları olmayan cebirsel kapalı ve meydana cebirsel sayı teorisi bu alanı olarak, rasyonel sayı , sayı alanları , sonlu cisimler , fonksiyon alanlar ve p -adic alanlar .
Tekillik teorisinin büyük bir kısmı cebirsel çeşitlerin tekilliklerine ayrılmıştır.
Hesaplamalı cebirsel geometri , bilgisayarların yükselişi ile cebirsel geometri ve bilgisayar cebirinin kesiştiği noktada ortaya çıkmış bir alandır . Temel olarak, açıkça verilen cebirsel çeşitlerin özelliklerinin incelenmesi için algoritma tasarımı ve yazılım geliştirmeden oluşur .

20. yüzyılda cebirsel geometrinin ana akımının gelişiminin çoğu, soyut bir cebirsel çerçeve içinde meydana geldi ve cebirsel çeşitlerin, çeşitliliği bir ortam koordinat uzayına yerleştirmenin herhangi bir özel yoluna bağlı olmayan "içsel" özelliklerine artan vurgu yapıldı; bu topoloji , diferansiyel ve karmaşık geometrideki gelişmelerle paralellik gösterir . Bu soyut cebirsel geometrinin Bir anahtar başarıdır Grothendieck 'ın düzeni teorisi biri kullanmanızı sağlar demeti teoriyi çalışmalarında kullanımı çok benzer bir şekilde cebirsel çeşitleri incelemek için Diferansiyel ve analitik manifoldu . Bu, nokta nosyonunu genişleterek elde edilir: Klasik cebirsel geometride, Hilbert'in Nullstellensatz'ı aracılığıyla, afin çeşitlilikteki bir nokta , koordinat halkasının maksimal ideali ile tanımlanabilirken, karşılık gelen afin şemanın noktalarının tümü asal idealdir. bu yüzüğün. Bu, böyle bir şemanın bir noktasının normal bir nokta veya bir alt değişken olabileceği anlamına gelir. Bu yaklaşım aynı zamanda, temel olarak karmaşık noktalarla ilgili olan klasik cebirsel geometrinin ve cebirsel sayı teorisinin dilinin ve araçlarının birleştirilmesini sağlar. Wiles'ın Fermat'ın Son Teoremi adlı uzun süredir devam eden varsayımının kanıtı , bu yaklaşımın gücüne bir örnektir.

Temel kavramlar

Eşzamanlı polinomların sıfırları

Küre ve eğimli daire

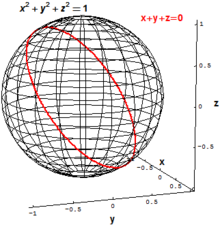
Klasik cebirsel geometride, ilgilenilen ana nesneler, bir veya daha fazla polinom denklemini aynı anda karşılayan tüm noktaların kümesi anlamına gelen, polinom koleksiyonlarının kaybolan kümeleridir . Örneğin, iki boyutlu küre , üç boyutlu olarak 1 yarıçaplı Öklid alan R ³ tüm noktaları (grubu olarak tanımlanabilir x , y , z ) ile

x^{2}+y^{2}+z^{2}-1=0.\,

R ^3'teki "eğimli" bir daire , iki polinom denklemini sağlayan tüm noktaların ( x , y , z ) kümesi olarak tanımlanabilir.

x^{2}+y^{2}+z^{2}-1=0,\,

{\görüntüleme stili x+y+z=0.\,}

afin çeşitleri

İlk önce bir k alanıyla başlıyoruz . Klasik cebirsel geometri, bu alan her zaman karmaşık sayılar oldu C , ama bunu sadece varsayarsak aynı sonuçların birçok doğruysa k olan cebirsel kapalı . A ⁿ ( k ) (veya daha basit olarak , k bağlamdan açık olduğunda A ⁿ ) ile gösterilen n boyutunun k üzerinde afin uzayını ele alıyoruz . Bir koordinat sistemi sabitlendiğinde, A ⁿ ( k ) k ^{n ile tanımlanabilir} . Çalışmıyor amacı k ⁿ bu bir "unutur" Vektör uzayı yapısını vurgulamak için k ⁿ taşır.

Bir fonksiyon f : A ^N → A ¹ olduğu söylenir polinom (ya da normal bir polinom varsa, olduğu, bir çok terimli şekilde yazılabilir ise) p içinde k [ x ₁ , ..., x _{, n} ] örneğin bu f ( E ) = p ( t ₁ , ..., t _{, n} ) her bir nokta için , M koordinatları ile ( t ₁ , ..., t _{, n} ) 'de A ^{, n} . Bir fonksiyonun polinom (veya düzenli) olma özelliği, A ^n'deki koordinat sisteminin seçimine bağlı değildir .

Bir koordinat sistemi seçildiği zaman, afin düzenli fonksiyonlar n -Space halkası ile tespit edilebilir polinom fonksiyonları olarak N fazla değişken k . Bu nedenle, A ⁿ üzerindeki düzenli fonksiyonlar kümesi, k [ A ⁿ ] ile gösterilen bir halkadır .

Bir polinomu o noktada değerlendirmek sıfır verirse, bir noktada yok olur deriz . S , k [ A ⁿ ] cinsinden bir polinomlar kümesi olsun . S ufuk grubu (ya da lokusu kaybolan ya da sıfır set ) dizi V ( S tüm noktaların) A ^{, n} burada her polinom içinde G yok olur. Sembolik,

V(S)=\{(t_{1},\dots ,t_{n})\mid p(t_{1},\dots ,t_{n})=0{\text{ tümü için } }p\S\}.\,

Bir alt kümesi, A ^{, n} olduğu V ( S ), bazı , S , bir adlandırılır cebirsel grubu . V açılımı çeşitli (cebirsel kümesinin belirli bir türü aşağıda tanımlanacaktır).

Bir alt Verilen U ait A ⁿ , tek oluşturursunuz polinomların kümesi kurtarabilirim? Eğer U olan herhangi bir alt kümesi A ^{, n} , tanımlar I ( u ) ufuk grubu içeren bütün polinomların grubu olduğu U . I temsil ideali : eğer iki polinomları f ve g her iki vanish U , ardından f + g yok olur, ilgili U , ve eğer h bir polinom, daha sonra HF ile kaybolur U , bu ı ( u ) her zaman polinom bir idealdir halka k [ A ⁿ ].

Sorulacak iki doğal soru:

Bir alt göz önüne alındığında U ve A ^{, n} , zaman olan , U = V ( I ( u ))?
Bir dizi S polinom verildiğinde, ne zaman S = I ( V ( S )) olur?

İlk sorunun cevabı , kapalı kümeleri cebirsel kümeler olan ve k [ A ⁿ ] ' nin cebirsel yapısını doğrudan yansıtan A ⁿ üzerinde bir topoloji olan Zariski topolojisi tanıtılarak sağlanır . O zaman U = V ( I ( U )) eğer ve sadece U bir cebirsel küme ise veya eşdeğerde bir Zariski-kapalı küme ise. İkinci sorunun cevabını Hilbert'in Nullstellensatz'ı veriyor . Formlarından birinde, I ( V ( S ))'nin S tarafından üretilen idealin radikali olduğunu söyler . Daha soyut bir dilde, iki kapatma operatörüne yol açan bir Galois bağlantısı vardır ; tanımlanabilirler ve doğal olarak teoride temel bir rol oynarlar; Örnek Galois bağlantısındaki üzerinde durulmuştur.

Çeşitli nedenlerle her zaman bir cebirsel U kümesine karşılık gelen idealin tamamıyla çalışmak istemeyebiliriz . Hilbert'in temel teoremi , k [ A ⁿ ] cinsinden ideallerin her zaman sonlu olarak üretildiğini ima eder .

Bir cebirsel küme, iki küçük cebirsel kümenin birleşimi olarak yazılamıyorsa, indirgenemez olarak adlandırılır . Herhangi bir cebirsel küme, indirgenemez cebirsel kümelerin sonlu birleşimidir ve bu ayrıştırma benzersizdir. Böylece elemanları cebirsel kümenin indirgenemez bileşenleri olarak adlandırılır . İndirgenemez bir cebirsel kümeye de çeşitlilik denir . Bir cebirsel kümenin, ancak ve ancak polinom halkasının bir asal idealinin kaybolan kümesi olarak tanımlanabiliyorsa bir çeşitlilik olduğu ortaya çıkıyor .

Bazı yazarlar cebirsel kümeler ve çeşitler arasında net bir ayrım yapmazlar ve gerektiğinde ayrım yapmak için indirgenemez çeşitlilik kullanırlar.

Düzenli fonksiyonlar

Tıpkı sürekli fonksiyonlar üzerindeki doğal haritalardır topolojik uzaylarda ve pürüzsüz fonksiyonlar üzerindeki doğal haritalar olan Diferensiyellenebilir manifoldlar , bir cebirsel sette fonksiyonların doğal sınıf denilen orada düzenli fonksiyonlar veya polinom fonksiyonlar . Bir cebirsel grubu üzerindeki normal bir işlev V içinde ihtiva edilen A ^{, n} kısıtlama olan V düzenli fonksiyon A ^{, n} . Karmaşık sayılar alanında tanımlanan bir cebirsel küme için düzenli fonksiyonlar düzgün ve hatta analitiktir .

Düzenli bir fonksiyonun her zaman çevre uzayına uzanmasını istemek doğal olmayan bir şekilde kısıtlayıcı görünebilir, ancak normal bir topolojik uzaydaki duruma çok benzer , burada Tietze genişleme teoremi kapalı bir altkümedeki sürekli bir fonksiyonun her zaman uzaya uzandığını garanti eder. ortam topolojik uzayı.

Afin uzaydaki düzenli fonksiyonlarda olduğu gibi, V üzerindeki düzenli fonksiyonlar, k [ V ] ile gösterdiğimiz bir halka oluşturur . Bu halka V'nin koordinat halkası olarak adlandırılır .

V üzerindeki düzenli fonksiyonlar, A ⁿ üzerindeki düzenli fonksiyonlardan geldiği için , koordinat halkaları arasında bir ilişki vardır. Spesifik olarak, eğer V üzerindeki normal bir fonksiyon k [ A ⁿ ]' deki f ve g fonksiyonlarının kısıtlanması ise , o zaman f - g V üzerinde null olan ve dolayısıyla I ( V )'ye ait olan bir polinom fonksiyonudur . Bu nedenle k [ V ile tespit edilebilir] k [ bir ⁿ ] / I ( V ).

Afin çeşitlerin morfizmi

Afin çeşitten A ^1'e düzenli fonksiyonları kullanarak, bir afin çeşitten diğerine düzenli haritalar tanımlayabiliriz . İlk önce, bir çeşitlilikten afin uzaya düzenli bir harita tanımlayacağız: V , A ⁿ içinde bulunan bir çeşitlilik olsun . V üzerinde m normal işlevi seçin ve bunları f ₁ , ..., f _{m olarak adlandırın} . Bir tanımlayan normal harita f den V için bir ^m sağlayarak f = ( f ₁ , ..., m _m ) . Başka bir deyişle, her f _i , f aralığının bir koordinatını belirler .

Eğer V 'çeşitli içerdiği olan bir ^m , biz demek f bir olan normal harita gelen V için V aralığı ise' f bulunan V '.

Düzenli haritaların tanımı cebirsel kümeler için de geçerlidir. Düzenli haritalar, tüm afin cebirsel kümelerin toplanmasını , nesnelerin afin cebirsel kümeler olduğu ve morfizmlerin düzenli haritalar olduğu bir kategoride topladıkları için morfizmler olarak da adlandırılır . Afin çeşitler, cebirsel kümeler kategorisinin bir alt kategorisidir.

Normal bir harita verilen gr dan V için V 've normal bir işlev f ve k [ V '], o zaman ön ∘ g ∈ k [ V ] . f → f ∘ g haritası , k [ V ′] ile k [ V ] arasında bir halka homomorfizmidir . Bunun aksine, her bir halka homomorfizmi k [ V '] ile k [ V ] düzenli bir ilk tanımlayan V için V '. Bu, cebirsel kümelerin kategorisi ile sonlu olarak oluşturulmuş indirgenmiş k- cebirlerinin karşıt kategorisi arasındaki kategorilerin denkliğini tanımlar . Bu denklik şema teorisinin başlangıç noktalarından biridir .

Rasyonel fonksiyon ve birational denklik

Önceki bölümlerin aksine, bu bölüm cebirsel kümelerle değil, yalnızca çeşitlerle ilgilidir. Öte yandan, tanımlar doğal olarak projektif çeşitlere kadar uzanır (bir sonraki bölüm), afin bir çeşittir ve projektif tamamlanması aynı işlev alanına sahiptir.

Eğer V , bir benzeşik çeşitli ise, kendi koordinat halka bir bir tamlık ve böylece sahip fraksiyonların alanı gösterilir k ( V ) ve adı rasyonel fonksiyonların alanı üzerinde V ya da kısa bir süre, fonksiyon alanına ait V . Onun elemanları için bir kısıtlama V arasında rasyonel fonksiyonların içeren afin uzay üzerinde V . Alan rasyonel fonksiyonu f değil V ancak tamamlayıcı altcins (a hiperyüzey) küçük birim f kaybolur.

Düzenli haritalar olduğu gibi, tek bir tanımlayabilir rasyonel harita çeşitli dan V çeşitli için V '. Düzenli haritalar olduğu gibi, gelen rasyonel haritalar V için V 'olarak tanımlanabilir alan homomorfizmalar gelen k ( V için)' k ( V ).

İki afin çeşit, her ikisinin de tanımlandığı bölgelerde, aralarında birbirinin tersi olan iki rasyonel fonksiyon varsa, çift yönlü eşdeğerdir . Eşdeğer olarak, eğer fonksiyon alanları izomorfik ise, çift yönlü olarak eşdeğerdirler.

Bir afin çeşitlilik, bir afin uzaya çift yönlü olarak eşdeğerse rasyonel bir çeşittir . Çeşitli bir itiraf Bu araç rasyonel parametreleştirmeyi bir olduğunu parametrizasyonları ile rasyonel fonksiyonların . Örneğin, denklem çemberi , parametrik denkleme sahip olduğu için rasyonel bir eğridir. $x^{2}+y^{2}-1=0$

x={\frac {2\,t}{1+t^{2}}}

y={\frac {1-t^{2}}{1+t^{2}}}\,,

bu aynı zamanda çizgiden daireye rasyonel bir harita olarak da görülebilir.

Tekilliklerin çözümlenmesi sorunu, her cebirsel çeşitliliğin, projektif tamamlaması tekil olmayan bir varyeteye çift yönlü olarak eşdeğer olup olmadığını bilmektir (ayrıca bkz . düzgün tamamlama ). 1964 yılında Heisuke Hironaka tarafından 0 karakteristiğinde olumlu olarak çözüldü ve henüz sonlu karakteristikte çözülmedi.

projektif çeşitlilik

Projektif uzayda parabol ( y = x ² , kırmızı) ve kübik ( y = x ³ , mavi)

İkinci, üçüncü ve dördüncü dereceden polinomların kökleri için formüllerin, gerçek sayıların karmaşık sayıların cebirsel olarak daha eksiksiz ayarına genişletilmesini önermesi gibi, cebirsel çeşitlerin birçok özelliği, afin uzayı geometrik olarak daha eksiksiz bir projektif uzaya genişletmeyi önerir. Karmaşık sayılar x ² +1 polinomunun kökü olan i sayısı toplanarak elde edilirken, projektif uzay, paralel doğruların buluşabileceği noktalar olan "sonsuzda" uygun noktalar eklenerek elde edilir.

Bunun nasıl olabileceğini görmek için V ( y - x ² ) çeşidini düşünün . Eğer çizersek , bir parabol elde ederiz . Şöyle x pozitif sonsuza giden noktaya kökenli çizginin eğimi ( x , x ² ), aynı zamanda olumlu bir sonsuz gider. As x negatif sonsuza gider, aynı doğrunun eğimi negatif sonsuza gider.

Bunu V ( y - x ³ ) çeşidiyle karşılaştırın . Bu bir kübik eğridir . As x pozitif sonsuza gider, noktasına kökenli doğrunun eğimi ( x , x ³ ) daha önce olduğu gibi pozitif sonsuza gider. Ama öncekinden farklı olarak, x negatif sonsuza giderken, aynı doğrunun eğimi de pozitif sonsuza gider; parabolün tam tersi. Dolayısıyla V'nin ( y - x ³ ) "sonsuzdaki" davranışı, V'nin ( y - x ² ) "sonsuzdaki" davranışından farklıdır .

Projektif düzlemde "sonsuzda" uzatmaları olan iki eğrinin yansıtmalı tamamlanmasının ele alınması, bu farkı nicelleştirmemize izin verir: parabolün sonsuzdaki noktası , teğeti sonsuzdaki doğru olan düzenli bir noktadır. , kübik eğrinin sonsuzluğundaki nokta ise bir tepe noktasıdır . Ayrıca, x ile parametrelendirildikleri için her iki eğri de rasyoneldir ve Riemann-Roch teoremi , kübik eğrinin afin uzaydaki tüm noktaları düzenli olduğu için sonsuzda olması gereken bir tekilliğe sahip olması gerektiğini ima eder.

Bu nedenle, cebirsel çeşitlerin, birasyonel eşdeğerlik ve tüm topolojik özellikler dahil olmak üzere birçok özelliği, "sonsuzdaki" davranışa bağlıdır ve bu nedenle, çeşitleri projektif uzayda incelemek doğaldır. Ayrıca, projektif tekniklerin tanıtılması, cebirsel geometrideki birçok teoremi daha basit ve keskin hale getirdi: Örneğin, Bézout'un iki çeşit arasındaki kesişme noktalarının sayısı hakkındaki teoremi , en keskin haliyle ancak yansıtmalı uzayda ifade edilebilir. Bu nedenlerden dolayı, projektif uzay cebirsel geometride temel bir rol oynar.

Günümüzde, yansıtmalı alan p ^{, n} boyut N , genellikle boyut afin boşlukta, menşe olarak kabul edilen bir noktasından geçen çizgilerin grubu olarak tanımlanır , n + 1 ya da eşdeğer a vektör hatlarının kümesine n + 1 boyutunun vektör uzayı . n +1 boyutundaki uzayda bir koordinat sistemi seçildiğinde , bir doğrunun tüm noktaları, k'nin bir elemanı ile çarpımına kadar aynı koordinat kümesine sahiptir . Bu tanımlar homojen koordinatlar bir noktasının P ^{, n} bir dizisi olarak , n + 1 baz alan elemanlarının k bir sıfır olmayan bir elemanı ile çarpma kadar tanımlandığı gibidir, k (tüm dizi için aynı).

n +1 değişkenli bir polinom , orijinden geçen bir doğrunun tüm noktalarında, ancak ve ancak homojen ise yok olur . Bu durumda, tek bir polinom söyler yok olur, karşılık gelen bir noktada P ⁿ . Bu, bir tanımlamasına izin verir yansıtmalı cebirsel set içinde P ^{, n} grubu olarak V ( f ₁ , ..., m _k ) , homojen polinomların sonlu grubu burada { f ₁ , ..., m _k } kaybolur. Afin cebirsel kümeler için olduğu gibi, yansıtmalı cebirsel kümeler ile onları tanımlayan indirgenmiş homojen idealler arasında bir eşleşme vardır . Projektif varyeteler olan tanımlayan İdeal asal yansıtmalı cebirsel kümeleridir. Başka bir deyişle, projektif çeşitlilik, homojen koordinat halkası bir integral alan olan, projektif koordinatlar halkası , dereceli halkanın veya homojen (indirgenmiş) ideal tarafından n + 1 değişkenlerdeki polinomların bölümü olarak tanımlanan projektif bir cebirsel kümedir. çeşitliliği tanımlar. Her yansıtmalı cebirsel küme, benzersiz bir şekilde, yansıtmalı çeşitlerin sonlu bir birleşimine ayrıştırılabilir.

Projektif bir çeşitlilikte düzgün bir şekilde tanımlanabilen tek düzenli işlevler, sabit işlevlerdir. Dolayısıyla bu kavram yansıtmalı durumlarda kullanılmaz. Öte yandan, rasyonel fonksiyonların alanı veya fonksiyon alanı , afin duruma benzer şekilde, homojen koordinat halkasında aynı derecede iki homojen elemanın bölümlerinin kümesi olarak tanımlanan faydalı bir kavramdır.

Gerçek cebirsel geometri

Gerçek cebirsel geometri, cebirsel çeşitlerin gerçek noktalarının incelenmesidir.

Gerçek sayıların alanının sıralı bir alan olduğu böyle bir çalışmada göz ardı edilemez. Örneğin, denklemin eğrisi bir if çemberidir , ancak if'nin herhangi bir reel noktası yoktur . Bundan, gerçek cebirsel geometrinin yalnızca gerçek cebirsel çeşitlerin incelenmesi değil, aynı zamanda polinom denklem sistemlerinin ve polinom eşitsizliklerinin çözümleri olan yarı cebirsel kümelerin çalışmasına genelleştirildiği sonucu çıkar . Örneğin, denklemin hiperbolünün bir dalı cebirsel bir çeşitlilik değil, ve veya tarafından ve ve ile tanımlanan bir yarı cebirsel kümedir . $x^{2}+y^{2}-a=0$ ${\görüntüleme stili a>0}$ ${\görüntüleme stili bir<0}$ ${\ Displaystyle xy-1=0}$ ${\ Displaystyle xy-1=0}$ ${\görüntüleme stili x>0}$ ${\ Displaystyle xy-1=0}$ $x+y>0$

Gerçek cebirsel geometrinin zorlu problemlerinden biri, çözülmemiş Hilbert'in on altıncı problemidir : 8. dereceden tekil olmayan bir düzlem eğrisinin ovalleri için hangi pozisyonların mümkün olduğuna karar verin .

Hesaplamalı cebirsel geometri

Hesaplamalı cebirsel geometrinin kökeni, Haziran 1979'da Fransa'nın Marsilya kentinde düzenlenen EUROSAM'79 (Uluslararası Sembolik ve Cebirsel Manipülasyon Sempozyumu) toplantısına tarihlenebilir . Bu toplantıda,

Dennis, S. Arnon gösterdi George E. Collins 'in silindirik cebirsel ayrışma , (CAD), yarı-cebirsel setleri topoloji hesaplama sağlar
Bruno Buchberger , Gröbner tabanlarını ve bunları hesaplamak için algoritmasını sundu ,
Daniel Lazard , beklenen çözüm sayısında esasen polinom olan ve dolayısıyla bilinmeyenlerin sayısında üstel olan bir hesaplama karmaşıklığına sahip homojen polinom denklem sistemlerini çözmek için yeni bir algoritma sundu . Bu algoritma, güçlü ilgilidir Macaulay 'in çok değişkenli sonuçtaki .

O zamandan beri, bu alandaki sonuçların çoğu, ya bu algoritmalardan birini kullanarak ya da geliştirerek ya da karmaşıklığı basitçe değişken sayısında üstel olan algoritmalar bularak bu öğelerden biri ya da birkaçı ile ilgilidir.

Son birkaç on yılda sayısal cebirsel geometri adı verilen sembolik yöntemleri tamamlayıcı bir matematiksel teori gövdesi geliştirilmiştir. Ana hesaplama yöntemi homotopi devamıdır . Bu, örneğin cebirsel geometri problemlerini çözmek için bir kayan nokta hesaplama modelini destekler .

Gröbner temeli

Bir Gröbner temeli , hesaplanması ideal tarafından tanımlanan afin cebirsel çeşitliliğin birçok özelliğinin çıkarılmasına izin veren bir polinom idealinin üreteçleri sistemidir .

Bir ideal verildiğinde, bir cebirsel küme V tanımlayan bir I :

V boştur (temel alanın cebirsel olarak kapalı bir uzantısı üzerinde), ancak ve ancak herhangi bir tek terimli sıralama için Gröbner tabanı {1}'ye düşürülürse.
Vasıtasıyla Hilbert serisi hesaplayabilir bir boyut ve derecesi ve V herhangi bir Gröbner temelinden I toplam derece rafine bir monomial sipariş için.
V'nin boyutu 0 ise, I'in herhangi bir Gröbner bazından V'nin noktaları (sayı olarak sonlu) hesaplanabilir (bkz . Polinom denklem sistemleri ).
Bir Gröbner tabanlı hesaplama, belirli bir hiperyüzeyde bulunan tüm indirgenemez bileşenlerin V'den çıkarılmasına izin verir .
Bir Gröbner tabanlı hesaplama , k birinci koordinatları üzerindeki izdüşüm ile V görüntüsünün Zariski kapanışını ve izdüşümün uygun olmadığı durumlarda görüntünün alt kümesini hesaplamaya izin verir .
Daha genel olarak Gröbner tabanlı hesaplamalar, görüntünün Zariski kapanışını ve V'nin rasyonel bir fonksiyonunun kritik noktalarını başka bir afin çeşitte hesaplamaya izin verir .

Gröbner temelli hesaplamalar, I'in birincil ayrışmasının veya V'nin indirgenemez bileşenlerini tanımlayan asal ideallerin doğrudan hesaplanmasına izin vermez , ancak bunun için çoğu algoritma Gröbner temel hesaplamasını içerir. Gröbner tabanlarına dayanmayan algoritmalar düzenli zincirler kullanır ancak bazı istisnai durumlarda Gröbner tabanlarına ihtiyaç duyabilir.

Gröbner bazlarının hesaplanmasının zor olduğu kabul edilir. Aslında, en kötü durumda, derecesi değişken sayısı bakımından iki kat üstel olan polinomlar ve yine iki kat üstel olan bir dizi polinom içerebilirler. Ancak, bu yalnızca en kötü durum karmaşıklığıdır ve Lazard'ın 1979 algoritmasının karmaşıklık sınırı sıklıkla geçerli olabilir. Faugère F5 algoritması , Lazard'ın 1979 algoritmasının bir gelişimi olarak görülebileceğinden, bu karmaşıklığı gerçekleştirir. En iyi uygulamaların 100'den fazla dereceli cebirsel kümelerle neredeyse rutin olarak hesaplamaya izin verdiği sonucu çıkar. Bu, şu anda bir Gröbner bazını hesaplamanın zorluğunun, sorunun içsel zorluğuyla güçlü bir şekilde ilişkili olduğu anlamına gelir.

Silindirik cebirsel ayrıştırma (CAD)

CAD, 1973 yılında G. Collins tarafından Tarski-Seidenberg teoremini gerçek sayılar üzerinden niceleyici eliminasyonunda kabul edilebilir bir karmaşıklıkla uygulamak için tanıtılan bir algoritmadır .

Bu teorem , atom formülleri polinom eşitlikleri veya gerçek katsayılı polinomlar arasındaki eşitsizlikler olan birinci mertebeden mantığın formülleriyle ilgilidir. Bu formüller ve böylece mantıksal operatör tarafından atom formüllerden imal edilebilir formüller ve (∧), ya da , (∨) değil , (¬) tüm (∀) ve var (∃). Tarski'nin teoremi, böyle bir formülden nicelik belirteci (∀, ∃) olmaksızın eşdeğer bir formül hesaplanabileceğini ileri sürer.

CAD'in karmaşıklığı, değişken sayısında iki kat üsteldir. Bu, CAD'nin teorik olarak, böyle bir formülle ifade edilebilen gerçek cebirsel geometrinin her problemini, yani açıkça verilen çeşitler ve yarı cebirsel kümelerle ilgili hemen hemen her problemi çözmeye izin verdiği anlamına gelir.

Gröbner tabanlı hesaplama, yalnızca nadir durumlarda iki kat üstel karmaşıklığa sahipken, CAD neredeyse her zaman bu yüksek karmaşıklığa sahiptir. Bu, girişte görünen polinomların çoğu doğrusal olmadıkça, dörtten fazla değişkenli problemleri çözemeyebileceği anlamına gelir.

1973'ten bu yana, bu konudaki araştırmaların çoğu ya CAD'i geliştirmeye ya da genel ilgi çeken özel durumlarda alternatif algoritmalar bulmaya ayrılmıştır.

Tekniğin bilinen durumuna bir örnek olarak, yarı cebirsel bir kümenin her bağlantılı bileşeninde en az bir nokta bulmak ve böylece yarı cebirsel bir kümenin boş olup olmadığını test etmek için etkili algoritmalar vardır. Öte yandan, CAD henüz pratikte bağlı bileşenlerin sayısını saymak için en iyi algoritmadır.

Asimptotik karmaşıklığa karşı pratik verimlilik

Hesaplamalı geometrinin temel genel algoritmaları, çift üstel en kötü durum karmaşıklığına sahiptir . Daha kesin olarak, eğer d giriş polinomlarının maksimum derecesi ve n değişkenlerin sayısı ise, karmaşıklıkları en fazla bir c sabiti için ve bazı girdiler için karmaşıklık en azından başka bir c ′ sabiti içindir . ${\görüntüleme stili d^{2^{cn}}}$ ${\görüntüleme stili d^{2^{c'n}}}$

20. yüzyılın son 20 yılında, belirli alt problemleri daha iyi bir karmaşıklıkla çözmek için çeşitli algoritmalar tanıtıldı. Bu algoritmaların çoğu bir karmaşıklığa sahiptir . ${\ Displaystyle d^{O(n^{2})}}$

Gröbner tabanları ile çözülen problemlerin bir alt problemini çözen bu algoritmalar arasında, afin çeşidin boş olup olmadığının test edilmesi ve sonlu sayıda çözümü olan homojen olmayan polinom sistemlerinin çözülmesinden bahsedilebilir. Bu tür algoritmalar nadiren uygulanır çünkü çoğu girdide Faugère'in F4 ve F5 algoritmaları daha iyi bir pratik verimliliğe ve muhtemelen benzer veya daha iyi bir karmaşıklığa sahiptir ( muhtemelen Gröbner tabanlı algoritmaların karmaşıklığının belirli bir girdi sınıfında değerlendirilmesi zor bir görev olduğu için). sadece birkaç özel durumda yapılmıştır).

CAD ile çözülen bir problemi çözen gerçek cebirsel geometrinin ana algoritmaları, yarı cebirsel kümelerin topolojisi ile ilgilidir. Bir örnek verebiliriz bağlı bileşenlerin sayısının sayılması , iki nokta aynı bileşenleri ise test veya bir bilgi işlem Whitney tabakalaşma bir cebirsel kümesinin . Karmaşıklıkları vardır , ancak O gösteriminin içerdiği sabit o kadar yüksektir ki, CAD tarafından etkin bir şekilde çözülen herhangi bir önemsiz sorunu çözmek için bunları kullanmak, dünyadaki tüm mevcut bilgi işlem gücünü kullanabilse bile imkansızdır. Bu nedenle, bu algoritmalar hiçbir zaman uygulanmamıştır ve bu, birlikte iyi bir asimptotik karmaşıklığa ve iyi bir pratik verimliliğe sahip algoritmaları aramak için aktif bir araştırma alanıdır. ${\ Displaystyle d^{O(n^{2})}}$

Soyut modern bakış açısı

Cebirsel geometriye yönelik modern yaklaşımlar, çeşitli genellik seviyelerindeki temel nesnelerin aralığını şemalara, biçimsel şemalara , ind şemalarına , cebirsel uzaylara , cebirsel yığınlara vb. yeniden tanımlar ve etkili bir şekilde genişletir . Buna duyulan ihtiyaç, zaten varyeteler teorisi içindeki faydalı fikirlerden kaynaklanmaktadır, örneğin Zariski'nin biçimsel işlevleri, yapı halkalarına nilpotent elementler dahil edilerek yerine getirilebilir; ilmeklerin ve yayların uzaylarını göz önünde bulundurarak, grup eylemleriyle bölümler oluşturmak ve doğal kesişim teorisi ve deformasyon teorisi için biçimsel zeminler geliştirmek, bazı diğer uzantılara yol açar.

En dikkat çekici şekilde, 1950'lerin sonlarında, cebirsel çeşitler Alexander Grothendieck'in şema kavramına dahil edildi . Onların yerel nesneler afin şemaları veya asal spektrumları lokal değişmeli unital halkaların kategorisine antiequivalent bir kategori oluşturan halkalı alanlardır bir saha üzerinde afin cebirsel çeşitlerinin kategori arasındaki ikiliği uzanan vardır k ve sonlu üretilmiş kategorisi indirgenmiş k -cebirleri. Yapıştırma Zariski topolojisi boyuncadır; yerel halkalı uzaylar kategorisi içinde yapıştırılabilir, ama aynı zamanda Yoneda gömme kullanılarak, afin şemalar kategorisine göre daha soyut küme ön-kasnakları kategorisi içinde yapıştırılabilir. Küme teorik anlamda Zariski topolojisi daha sonra bir Grothendieck topolojisi ile değiştirilir . Grothendieck, Grothendieck topolojilerini, kaba Zariski topolojisinden, yani étale topolojisinden ve iki düz Grothendieck topolojisinden: fppf ve fpqc; günümüzde Nisnevich topolojisi de dahil olmak üzere diğer bazı örnekler öne çıktı . Demetler ayrıca Grothendieck anlamında yığınlara genelleştirilebilir, genellikle Artin yığınlarına ve hatta daha ince olan Deligne-Mumford yığınlarına yol açan bazı ek temsil edilebilirlik koşullarıyla , her ikisi de genellikle cebirsel yığınlar olarak adlandırılır.

Bazen diğer cebirsel siteler, afin şemalar kategorisinin yerini alır. Örneğin Nikolai Durov , genelleştirilmiş bir cebirsel geometride yerel nesnelerin bir genellemesi olarak değişmeli cebirsel monadları tanıttı. Bir sürümleri tropikal geometri bir bölgesinin, mutlak geometrinin bir elementin bir alan ve bir cebirsel analog üzerinde Arakelov geometrisine bu kurulumda gerçekleştirilmiştir.

Her cebir çeşidinin kendi cebirsel geometrisine sahip olduğu evrensel cebirsel geometri için başka bir biçimsel genelleme mümkündür . Cebir çeşitliliği terimi , cebirsel çeşitlilik ile karıştırılmamalıdır .

Şemaların, yığınların ve genellemelerin dili, geometrik kavramlarla başa çıkmanın değerli bir yolu olduğunu kanıtladı ve modern cebirsel geometrinin temel taşları haline geldi.

Cebirsel yığınlar daha da genelleştirilebilir ve deformasyon teorisi ve kesişim teorisi gibi birçok pratik soru için bu genellikle en doğal yaklaşımdır. Değişmeli halkaları diferansiyel dereceli değişmeli cebirlerin bir sonsuz kategorisiyle veya basit değişmeli halkaların veya benzer bir kategorinin uygun bir Grothendieck varyantı ile değiştirilmesiyle, afin şemaların Grothendieck bölgesi , türetilmiş afin şemaların daha yüksek bir kategorik bölgesine genişletilebilir. topoloji. Ayrıca kümelerin ön kasnakları basit kümelerin (veya sonsuz grupoidlerin) ön kasnakları ile değiştirilebilir. Daha sonra, uygun bir homotopik makinenin varlığında, bir demet aksiyomunun (ve cebirsel olmak gerekirse, tümevarımsal olarak bir dizi) belirli sonsuz kategorik versiyonunu karşılayan türetilmiş afin şemalarının sonsuzluk kategorisi üzerinde bir ön demet gibi bir türetilmiş yığın kavramı geliştirilebilir. temsil edilebilirlik koşulları). Quillen model kategorileri , Segal kategorileri ve yarı kategoriler , Andre Hirschowitz, Bertrand Toën , Gabrielle Vezzosi, Michel Vaquié ve diğerleri dahil olmak üzere Carlos Simpson okulu tarafından tanıtılan , türetilmiş cebirsel geometriyi sağlayan bunu resmileştirmek için en sık kullanılan araçlardan bazılarıdır; ve Jacob Lurie , Bertrand Toën ve Gabrielle Vezzosi tarafından daha da geliştirildi . A-sonsuz kategorilerini kullanan türetilmiş cebirsel geometrinin bir başka (değişmeli olmayan) versiyonu, 1990'ların başlarında Maxim Kontsevich ve takipçileri tarafından geliştirilmiştir .

Tarih

16. yüzyıldan önce

Cebirsel geometrinin bazı kökleri, MÖ 5. yüzyıldan Helenistik Yunanlıların çalışmalarına kadar uzanır. Delian sorun , örneğin, bir uzunluk oluşturmak için olan x yan küp olacak şekilde x dikdörtgen bir kutu ile aynı hacim içermiş ve bir ²b verilen iki taraf için bir ve b . Menaechmus (yaklaşık MÖ 350), ay = x ² ve xy = ab düzlem konik çiftlerini keserek sorunu geometrik olarak ele aldı . MÖ 3. yüzyılda, Arşimet ve Apollonius , koordinatları kullanarak konik kesitler üzerinde sistematik olarak ek problemler üzerinde çalıştılar . MS 10. yüzyılda İbnü'l-Heysem de dahil olmak üzere Ortaçağ Müslüman matematikçileri , belirli kübik denklemleri tamamen cebirsel yollarla çözdüler ve ardından sonuçları geometrik olarak yorumladılar. Pers matematikçi Ömer Hayyam'ın (doğum 1048 AD) çözümü için bir yöntem keşfetti kübik denklemleri bir daire ile bir parabol kesişen tarafından ve kübik denklemlerin genel teorisi gebe ilk olmuş gibi görünmektedir. Birkaç yıl Ömer Hayyam sonra, Sharaf al-Din el-Tusi 'ın denklemler üzerinde Risalesi 'cebirsel geometrinin başlangıcını açılışını' olarak Roshdi Rashed tarafından tarif edilmiştir. Bu, denklemler aracılığıyla eğrilerin incelenmesinin on yedinci yüzyılda Descartes ile ortaya çıktığını iddia eden Jeffrey Oaks tarafından eleştirildi.

Rönesans

Cebirsel problemlere geometrik yapıların uygulanmasına yönelik bu tür teknikler, Gerolamo Cardano ve Niccolò Fontana "Tartaglia" gibi bir dizi Rönesans matematikçisi tarafından kübik denklem çalışmalarında benimsenmiştir . Yapı problemlerine cebirsel yaklaşımdan ziyade geometrik yaklaşım, 16. ve 17. yüzyıl matematikçilerinin çoğu, özellikle geometride cebirsel ve analitik yöntemlerin kullanımına karşı çıkan Blaise Pascal tarafından tercih edildi . Fransız matematikçiler Franciscus Vieta ve daha sonra René Descartes ve Pierre de Fermat , koordinat geometrisinin tanıtılması yoluyla inşaat problemleriyle ilgili geleneksel düşünce biçiminde devrim yarattı . Öncelikli olarak, Diophantine denklemleri (Fermat durumunda) tarafından tanımlananlar gibi cebirsel eğrilerin özellikleri ve konikler ve kübikler (Descartes durumunda) üzerine klasik Yunan eserlerinin cebirsel yeniden formülasyonu ile ilgilendiler.

Aynı dönemde Blaise Pascal ve Gérard Desargues geometriye farklı bir perspektiften yaklaşarak projektif geometrinin sentetik kavramlarını geliştirdiler . Pascal ve Desargues de eğrileri inceledi, ancak tamamen geometrik bir bakış açısıyla: Yunan cetvelinin ve pusula yapısının analoğu . Nihayetinde, Descartes ve Fermat'ın analitik geometrisi galip geldi, çünkü 18. yüzyıl matematikçilerine Newton ve Leibniz'in yeni hesabını kullanarak fiziksel problemleri incelemek için gereken somut nicel araçları sağladı . Bununla birlikte, 18. yüzyılın sonunda, koordinat geometrisinin cebirsel karakterinin çoğu , Lagrange ve Euler'in sonsuz küçükler hesabı tarafından kapsandı .

19. ve 20. yüzyılın başlarında

Eski cebirsel fikirleri geometrik kıvrıma geri getirmek için, Öklidyen olmayan geometrinin ve Abelian integrallerin 19. yüzyıldaki eşzamanlı gelişmelerini aldı . Bu yeni gelişmelerin ilki , projektif uzayın genelleştirilmiş metrik özelliklerini belirlemeye çalışan Edmond Laguerre ve Arthur Cayley tarafından ele alındı . Cayley, homojen polinom formları fikrini ve daha özel olarak ikinci dereceden formları projektif uzayda tanıttı . Daha sonra, Felix Klein , bir uzaydaki geometrinin, uzaydaki belirli bir dönüşüm sınıfında kodlandığı bakış açısından projektif geometriyi (diğer geometri türleri ile birlikte) inceledi . 19. yüzyılın sonunda, projektif geometriler, projeksiyonlu uzaydaki figürler üzerinde daha genel dönüşüm türlerini inceliyorlardı. Normalde yansıtmalı uzayda temel Kleincı geometriyi verdiği kabul edilen yansıtmalı doğrusal dönüşümler yerine , kendilerini daha yüksek dereceli çift yönlü dönüşümlerle de ilgilendirdiler . Bu daha zayıf uyum kavramı daha sonra 20. yüzyıl İtalyan cebirsel geometri okulunun üyelerini cebirsel yüzeyleri çift yönlü izomorfizme kadar sınıflandırmaya yönlendirecektir .

19. yüzyılın başlarındaki ikinci gelişme, Abelian integrallerinin gelişimi, Bernhard Riemann'ı Riemann yüzeylerinin gelişimine götürecekti .

Aynı dönemde cebirsel geometrinin değişmeli cebir yoluyla cebirleştirilmesi başladı . Bu yönde öne çıkan sonuçlar Hilbert'in baz teoremi ve Hilbert'in Nullstellensatz cebirsel geometri ve değişmeli cebir arasında bir bağlantı temeli olan, ve Macaulay 'in çok değişkenli elde edilen temelidir, eleme teorisi . Muhtemelen çok değişkenli bileşkenlerin ima ettiği hesaplamanın boyutu nedeniyle, eliminasyon teorisi 20. yüzyılın ortalarında tekillik teorisi ve hesaplamalı cebirsel geometri tarafından yenilenene kadar unutuldu .

20. yüzyıl

BL van der Waerden , Oscar Zariski ve André Weil , değerleme teorisi ve idealler teorisi dahil olmak üzere çağdaş değişmeli cebire dayanan cebirsel geometri için bir temel geliştirdi . Hedeflerden biri, İtalyan cebirsel geometri okulunun sonuçlarını kanıtlamak için titiz bir çerçeve vermekti . Özellikle, bu okul , 1930'larda bu yazarlar tarafından ilk kez verilen, kesin bir tanım olmaksızın jenerik nokta kavramını sistematik olarak kullandı .

1950'ler ve 1960'larda Jean-Pierre Serre ve Alexander Grothendieck demet teorisini kullanarak temelleri yeniden şekillendirdiler . Daha sonra, yaklaşık 1960'tan itibaren ve büyük ölçüde Grothendieck tarafından yönetilen şemalar fikri, çok incelikli bir homolojik teknikler aygıtıyla birlikte geliştirildi . On yıllık hızlı gelişmeden sonra, alan 1970'lerde stabilize oldu ve hem sayı teorisine hem de cebirsel çeşitler, tekillikler , modüller ve biçimsel modüller hakkında daha klasik geometrik sorulara yeni uygulamalar yapıldı .

Doğrudan tanımlayıcı denklemlerinden kolayca anlaşılamayan önemli bir çeşit sınıfı , noktaları bir değişmeli grup oluşturan projektif çeşitler olan değişmeli çeşitlerdir . Prototip örnekler, zengin bir teoriye sahip eliptik eğrilerdir . Fermat'ın Son Teoreminin ispatında etkiliydiler ve eliptik eğri kriptografisinde de kullanılıyorlar .

Çeşitlerle ilgili genel ifadelerle ilgilenen cebirsel geometrinin soyut eğilimine paralel olarak, yeni hesaplamalı cebirsel geometri alanına yol açan somut olarak verilen çeşitlerle etkili hesaplama yöntemleri de geliştirilmiştir. Bu alanın kuruluş yöntemlerinden biri , 1965'te Bruno Buchberger tarafından tanıtılan Gröbner tabanları teorisidir. Daha özel olarak gerçek cebirsel geometriye ayrılmış bir başka kuruluş yöntemi, 1973'te George E. Collins tarafından tanıtılan silindirik cebirsel ayrıştırmadır .

Ayrıca bakınız: türetilmiş cebirsel geometri .

Analitik Geometri

Bir analitik çeşitlilik içeren çeşitli denklemlerin ortak çözümler kümesi olarak da tanımlanır analitik fonksiyonlar . Dahil edilen gerçek veya karmaşık cebirsel çeşitlilik kavramına benzer . Herhangi bir karmaşık manifold analitik bir çeşittir. Analitik çeşitlerin tekil noktaları olabileceğinden , tüm analitik çeşitler manifold değildir.

Modern analitik geometri, Jean-Pierre Serre'nin Fransızca'da Cebirsel geometri ve analitik geometri anlamına gelen GAGA adlı makalesinde gösterildiği gibi, esasen gerçek ve karmaşık cebirsel geometriye eşdeğerdir . Bununla birlikte, ispat yöntemleri oldukça farklı olduğundan ve cebirsel geometri, sonlu karakteristikte geometriyi de içerdiğinden, iki alan farklı kalır .

Uygulamalar

Cebirsel geometri artık istatistik , kontrol teorisi , robotik , hata düzeltme kodları , filogenetik ve geometrik modelleme alanlarında uygulama bulmaktadır . Ayrıca sicim teorisi , oyun teorisi , grafik eşleştirmeleri , solitonlar ve tamsayı programlamaya da bağlantılar vardır .

Ayrıca bakınız

Notlar

Referanslar

Kaynaklar

Kline, M. (1972). Antik Çağdan Modern Zamana Matematiksel Düşünce . Cilt 1. Oxford University Press. ISBN'si 0195061357. |volume=fazladan metin var ( yardım )

daha fazla okuma

Planlardan önce gelen bazı klasik ders kitapları

van der Waerden, BL (1945). Cebirsel Geometride Einfuehrung . Dover .
Hodge, WVD ; Pedo, Daniel (1994). Cebirsel Geometri Yöntemleri Cilt 1 . Cambridge Üniversitesi Yayınları . ISBN'si 978-0-521-46900-5. Zbl 0796.14001 .
Hodge, WVD ; Pedo, Daniel (1994). Cebirsel Geometri Yöntemleri Cilt 2 . Cambridge Üniversitesi Yayınları . ISBN'si 978-0-521-46901-2. Zbl 0796.14002 .
Hodge, WVD ; Pedo, Daniel (1994). Cebirsel Geometri Yöntemleri Cilt 3 . Cambridge Üniversitesi Yayınları . ISBN'si 978-0-521-46775-9. Zbl 0796.14003 .

Planların dilini kullanmayan modern ders kitapları

Garry, Thomas; ve diğerleri (2013). Cebirsel Geometri Bir Problem Çözme Yaklaşımı . Amerikan Matematik Derneği . ISBN'si 978-0-821-89396-8.
Griffiths, Phillip ; Harris, Joe (1994). Cebirsel Geometrinin İlkeleri . Wiley-Interscience . ISBN'si 978-0-471-05059-9. Zbl 0836.14001 .
Harris, Joe (1995). Cebirsel Geometri İlk Ders . Springer-Verlag . ISBN'si 978-0-387-97716-4. Zbl 0779.14001 .
Mumford, David (1995). Cebirsel Geometri I Karmaşık Projektif Çeşitleri (2. baskı). Springer-Verlag . ISBN'si 978-3-540-58657-9. Zbl 0821.14001 .
Reid, Miles (1988). Lisans Cebirsel Geometri . Cambridge Üniversitesi Yayınları . ISBN'si 978-0-521-35662-6. Zbl 0701.14001 .
Shafarevich, İgor (1995). Temel Cebirsel Geometri I Projektif Uzayda Çeşitleri (2. baskı). Springer-Verlag . ISBN'si 978-0-387-54812-8. Zbl 0797.14001 .

Hesaplamalı cebirsel geometri ders kitapları

Cox, David A .; Küçük John; O'Shea, Donal (1997). İdealler, Çeşitler ve Algoritmalar (2. baskı). Springer-Verlag . ISBN'si 978-0-387-94680-1. Zbl 0861.13012 .
Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006). Gerçek cebirsel geometride algoritmalar . Springer-Verlag .
González-Vega, Laureano; Recio, Tomas (1996). Cebirsel geometride algoritmalar ve uygulamaları . Birkhaüser.
Elkadi, Mohamed; Murrain, Bernard; Piene, Ragni, ed. (2006). Cebirsel geometri ve geometrik modelleme . Springer-Verlag .
Dickenstein, Alicia ; Schreyer, Frank-Olaf; Sommese, Andrew J., ed. (2008). Cebirsel Geometride Algoritmalar . Matematikte IMA Ciltleri ve Uygulamaları. 146 . Springer . ISBN'si 9780387751559. LCCN 2007938208 .
Cox, David A. ; Küçük, John B.; O'Shea, Donal (1998). Cebirsel geometriyi kullanma . Springer-Verlag .
Kavite, Bob F.; Johnson, Jeremy R. (1998). Niceleyici eleme ve silindirik cebirsel ayrıştırma . Springer-Verlag .

Ders kitapları ve şemalar için referanslar

Eisenbud, David ; Harris, Joe (1998). Şemaların Geometrisi . Springer-Verlag . ISBN'si 978-0-387-98637-1. Zbl 0960.14002 .
Grothendieck, Alexander (1960). Éléments de géométrie algébrique . Yayınlar Mathématiques de l'IHÉS . Zbl 0118.36206 .
Grothendieck, İskender ; Dieudonne, Jean Alexandre (1971). Éléments de géométrie algébrique . 1 (2. baskı). Springer-Verlag . ISBN'si 978-3-540-05113-8. Zbl 0203.23301 .
Hartshorne, Robin (1977). Cebirsel Geometri . Springer-Verlag . ISBN'si 978-0-387-90244-9. Zbl 0367.14001 .
Mumford, David (1999). Çeşitlerin ve Şemaların Kırmızı Kitabı Eğriler ve Jacobianları Üzerine Michigan Derslerini içerir (2. baskı). Springer-Verlag . ISBN'si 978-3-540-63293-1. Zbl 0945.14001 .
Shafarevich, İgor (1995). Temel Cebirsel Geometri II Şemaları ve karmaşık manifoldlar (2. baskı). Springer-Verlag . ISBN'si 978-3-540-57554-2. Zbl 0797.14002 .

Dış bağlantılar

Cebirsel Geometrinin Temelleri, Ravi Vakil, 808 s.
PlanetMath üzerinde cebirsel geometri girişi
Van der Waerden ders kitabının İngilizce çevirisi
Dieudonné, Jean (3 Mart 1972). "Cebirsel Geometri Tarihi" . YouTube üzerinden Wisconsin-Milwaukee Üniversitesi Matematik Bölümü'nde konuşun .
Yığın Projesi , cebirsel yığınlar ve cebirsel geometri üzerinde açık kaynaklı bir ders kitabı ve referans çalışması

Languages

In other projects